Numerical integration.

One-dimensional numerical integration using the NumericalIntegration C++ library.

numerical-integration

One-dimensional numerical integration using the 'NumericalIntegration' C++ library.

Example. Integrate x² between 0 and 1 with desired absolute error 0, desired relative error 1e-5 and using 200 subdivisions. Exact value: 1/3.

example :: IO IntegralResult -- value, error estimate, error code
example = integration (\x -> x*x) 0 1 0.0 1e-5 200
-- IntegralResult {
--   _value = 0.3333333333333334, 
--   _error = 3.7007434154171895e-15, 
--   _code = 0
-- }

The error code 0 indicates the success.

A highly oscillatory function. The function shown below is highly oscillatory. It is know that the exact value of its integral from 0 to 1 is π exp(-10) / 2 ≈ 7.131404e-05.

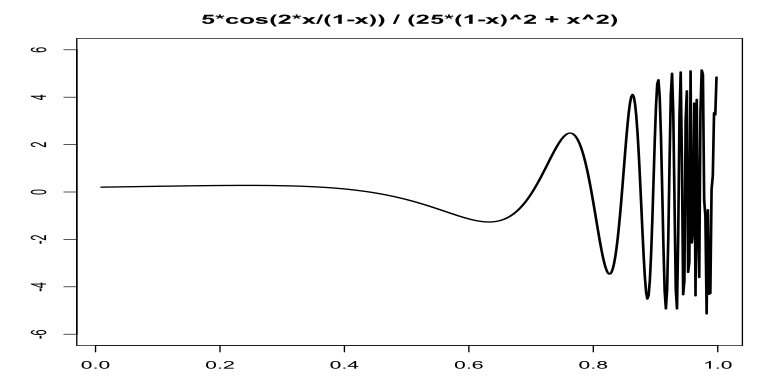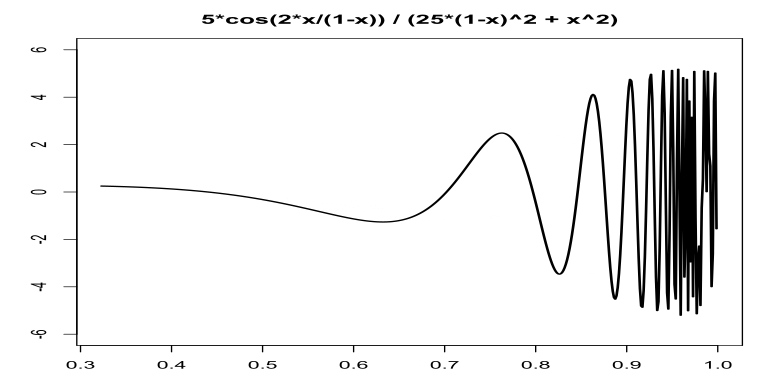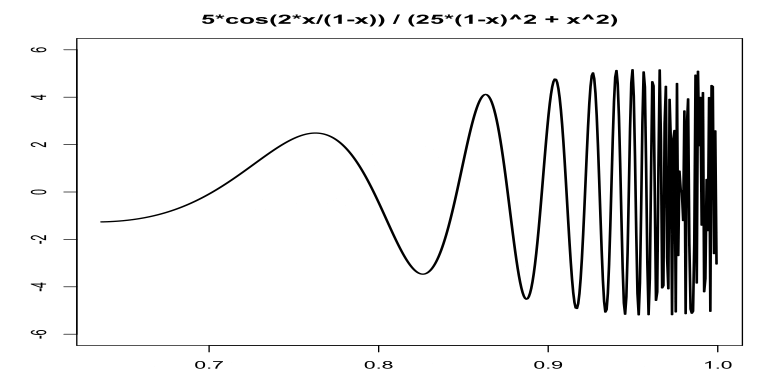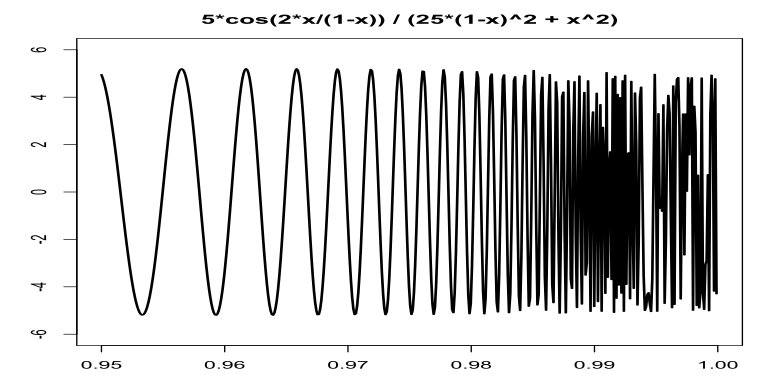
Let's try to evaluate it with R with 200000 subdivisions.

f <- function(x) {
  5*cos(2*x/(1-x)) / (25*(1-x)**2 + x**2)
}
integrate(f, 0, 1, subdivisions = 200000)
# 7.76249e-05 with absolute error < 3.7e-05

R does not complain, however the result is not very good.

Now let's try with the present library, with 100000 subdivisions.

intgr :: IO IntegralResult 
intgr = integration (\t -> 5 * cos(2*t/(1-t)) / (25*(1-t)**2 + t**2)) 0 1 0.0 1e-4 100000
-- IntegralResult {
--    _value = 7.131328051415349e-5, 
--    _error = 4.991435083852171e-7, 
--    _code = 2
-- }

As compared to R, the computation is very slow. But the result is quite better. Note that the error code is 2, thereby indicating a failure of convergence. So let's try 250000 subdivisions. This will take a while.

intgr :: IO IntegralResult 
intgr = integration (\t -> 5 * cos(2*t/(1-t)) / (25*(1-t)**2 + t**2)) 0 1 0.0 1e-4 250000
-- IntegralResult {
--   _value = 7.131328051415349e-5, 
--   _error = 4.991435083852171e-7, 
--   _code = 2
-- }

The result is the same!

The tanh-sinh procedure. I don't master the Haskell library 'integration' but I give it a try below. It implements the tanh-sinh quadrature.

import Numeric.Integration.TanhSinh

tanhsinh :: Result
tanhsinh = absolute 1e-6 $ parTrap (\t -> 5 * cos(2*t/(1-t)) / (25*(1-t)**2 + t**2)) 0 1
-- Result {
--   result = -6.463872646093162e-3, 
--   errorEstimate = 2.577460946077898e-2, 
--   evaluations = 769
-- }

The result is totally wrong, which is not surprising in view of the weak number of evaluations. But again, I don't master this library so I will not conclude anything from this result.