Posit Numbers.

The Posit Number format attempting to conform to the Posit Standard Versions 3.2 and 2022. Where Real numbers are approximated by `Maybe Rational` and sampled in a similar way to the projective real line.

posit 2022.2.0.0

The Posit Standard 2022, and Posit Standard 3.2, where Real numbers are approximated by Maybe Rational. The Posit Numbers are a drop in replacement for Float or Double mapped to a 2's complement integer type; smoothly and with tapering precision, in a similar way to the projective real line. The 'posit' library implements the following standard classes:

• Show
• Eq
• Ord -- compare as an integer representation
• Num -- Addition, subtraction, multiplication, and other operations
• Enum -- Successor and Predecessor
• Fractional -- division, divide by zero is Not a Real (NaR) number
• Real
• Bounded
• FusedOps -- dot product and others
• Convertable -- Conversions between different posit formats
• AltShow
• Read
• Storable -- Formats for binary data, for computation and data interchange
• Random
• Uniform
• RealFrac
• RealFloat
• Floating -- Mathematical functions such as logarithm, exponential, trigonometric, and hyperbolic functions. Warning! May induce trance.

The Posits are indexed by the type (es :: ES) where exponent size and word size are related. In posit-3.2 es is instantiated as Z, I, II, III, IV, V. In posit-2022 es is instantiated as Z_2022, I_2022, II_2022, III_2022, IV_2022, V_2022. The word size (in bits) of the value is = 8 * 2^es, that is 2^es bytes. The Types: 'Posit8', 'Posit16', 'Posit32', 'Posit64', 'Posit128', and 'Posit256' as well as, 'P8', 'P16', 'P32', 'P64', 'P128', and 'P256' are implemented and include a couple of auxiliary classes, like AltShow, AltFloating, and FusedOps. So, 3.2 scales by dynamic range, 2022 scales by precision.

class AltShow a where
  -- Display the Posit in its Binary Representation
  displayBinary :: a -> String
  -- Display the Posit in its Integral Representation
  displayIntegral :: a -> String
  -- Display the Posit as a Rational
  displayRational :: a -> String
  -- Display the Posit as a Decimal until the Repented occurs
  displayDecimal :: a -> String

class AltFloating p where
  machEps :: p  -- Machine Epsilon near 1.0
  approxEq :: p -> p -> Bool
  goldenRatio :: p
  hypot2 :: p -> p -> p
  hypot3 :: p -> p -> p -> p
  hypot4 :: p -> p -> p -> p -> p

The 'FusedOps' class has been updated with rewrite rules, enabled by the --flag posit:do-rewrite flag. When the flag is enabled, the ghc compiler will match the pattern and then automatically rewrite with the fused operation.

class Num a => FusedOps a where
  -- |Fused Multiply Add: (a * b) + c
  fma :: a -> a -> a -> a
  -- |Fused Add Multiply: (a + b) * c
  fam :: a -> a -> a -> a
  -- |Fused Multiply Multiply Subtract: (a * b) - (c * d)
  fmms :: a -> a -> a -> a -> a
  -- |Fused Sum of 3 values: a + b + c
  fsum3 :: a -> a -> a -> a
  -- |Fused Sum of 4 values: a + b + c + d
  fsum4 :: a -> a -> a -> a -> a
  -- |Fused Sum of a List of Posits
  fsumL :: Foldable t => t a -> a
  -- |Fused Dot Product of 3 element vector: (a1 * b1) + (a2 * b2) + (a3 * b3)
  fdot3 :: a -> a -> a -> a -> a -> a -> a
  -- |Fused Dot Product of 4 element veector: (a0 * b0) + (a1 * b1) + (a2 * b2) + (a3 * b3)
  fdot4 :: a -> a -> a -> a -> a -> a -> a -> a -> a
  -- |Fused Dot Product of Two Lists
  fdotL :: Foldable t => t a -> t a -> a
  -- |Fused Subtract Multiply: a - (b * c)
  fsm :: a -> a -> a -> a

The Posit type is 'Convertible' between other Posit lengths.

class Convertible a b where
  convert :: a -> b

The Posit Library is built on top of two of the most excellent libraries: data-dword, and scientific. The 'data-dword' library provides the underlining machine word representation, it can provide 2^es word size, 2's complement fixed length integers. The 'scientific' library provides 'read' and 'show' instances.

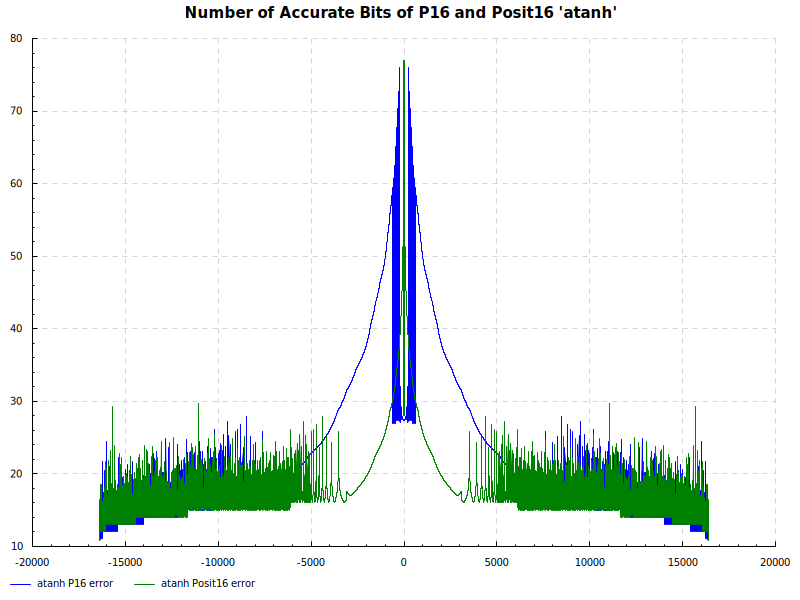
The Elementary Functions for this posit library are implemented natively using the next larger posit number. P16 and Posit16 numbers are tested exhaustively against Double Precision numbers as the orical. The results are below:

Number of Accurate Bits exp: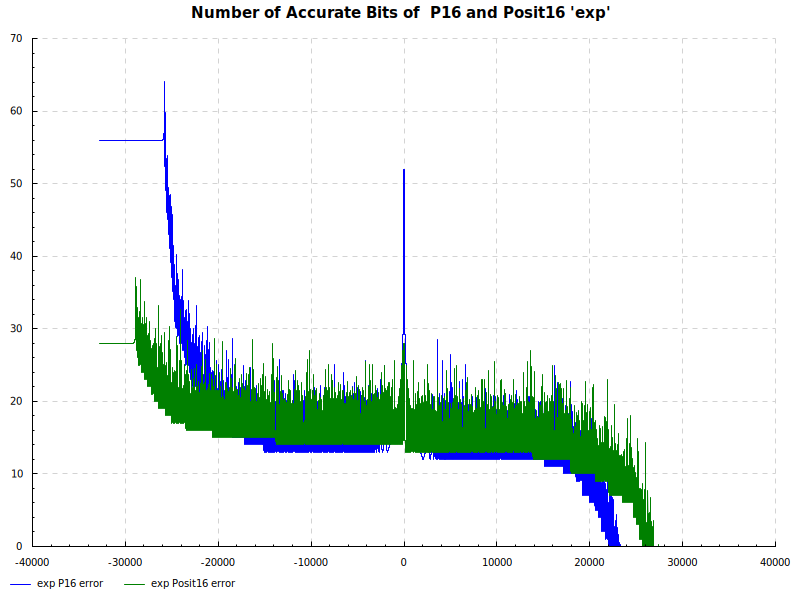

Number of Accurate Bits log: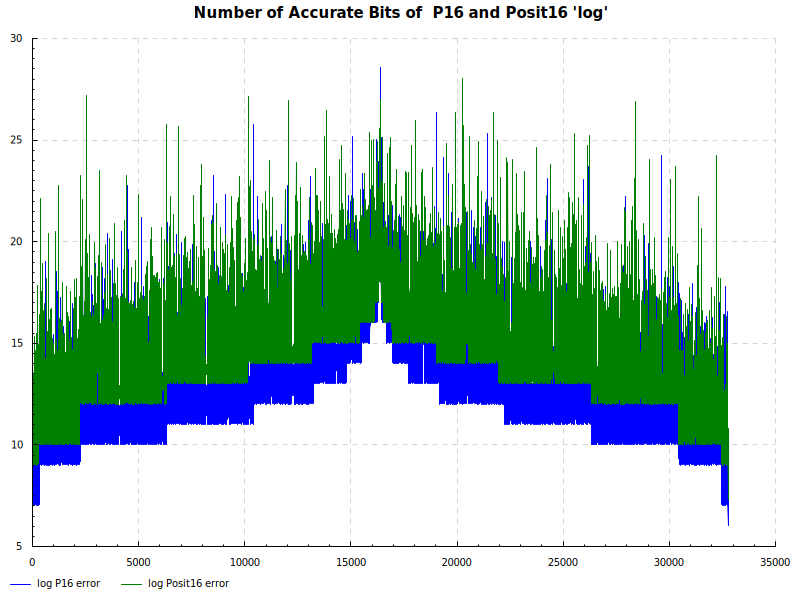

Number of Accurate Bits sqrt: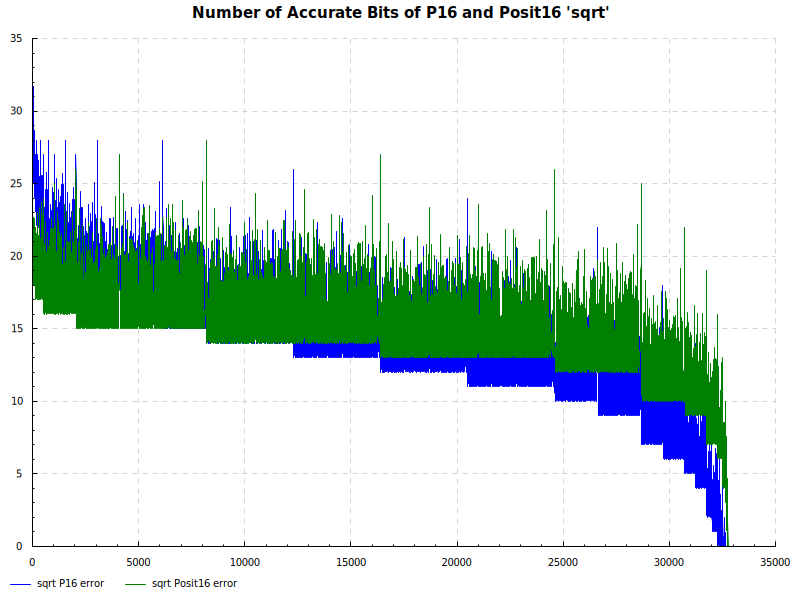

Number of Accurate Bits sin: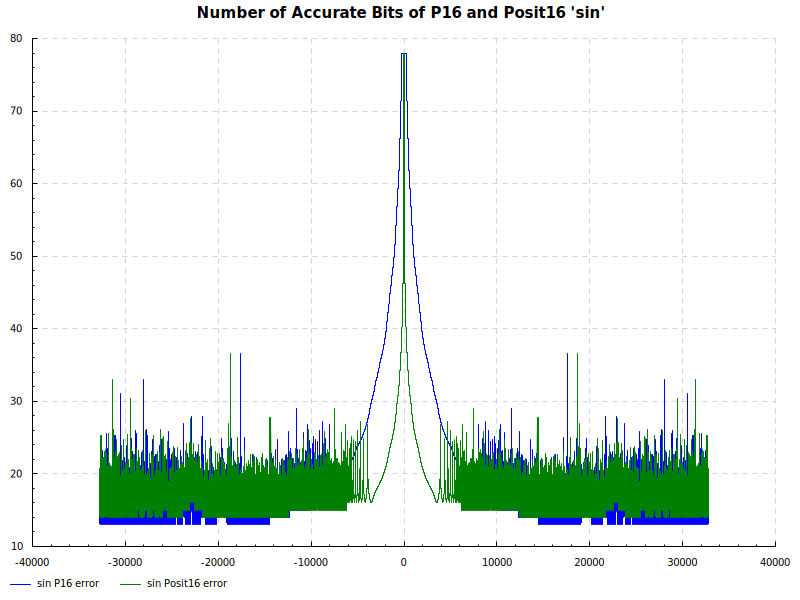

Number of Accurate Bits cos: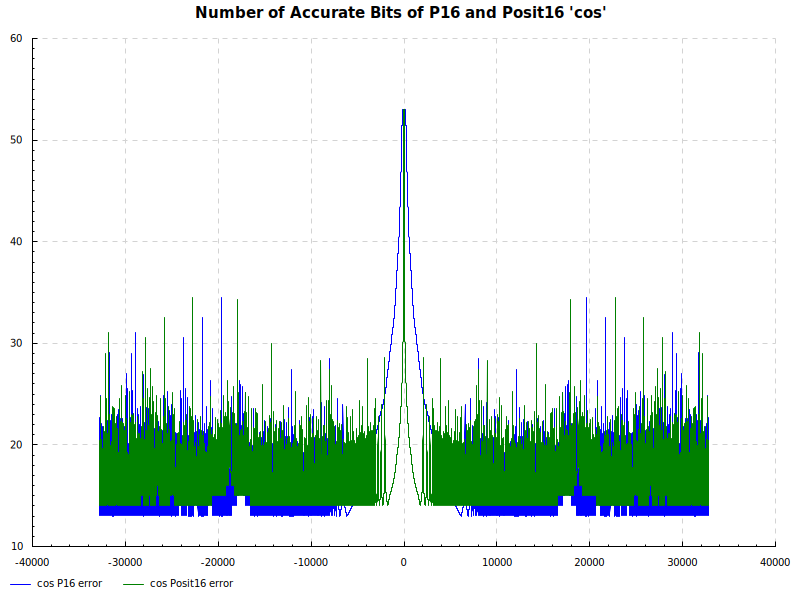

Number of Accurate Bits asin: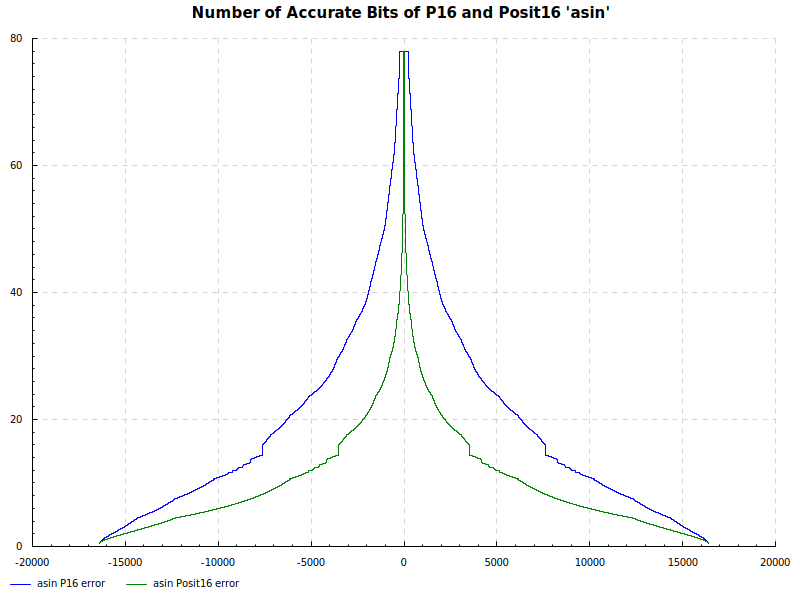

Number of Accurate Bits acos: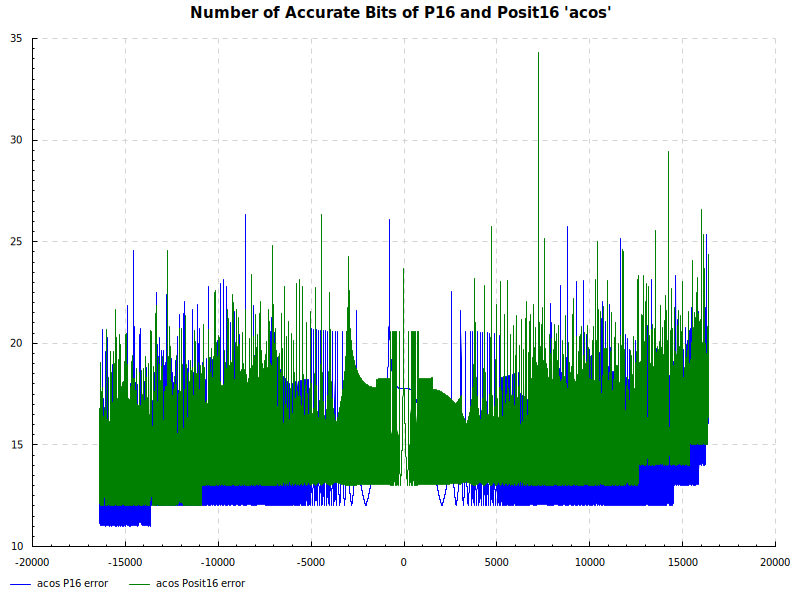

Number of Accurate Bits atan: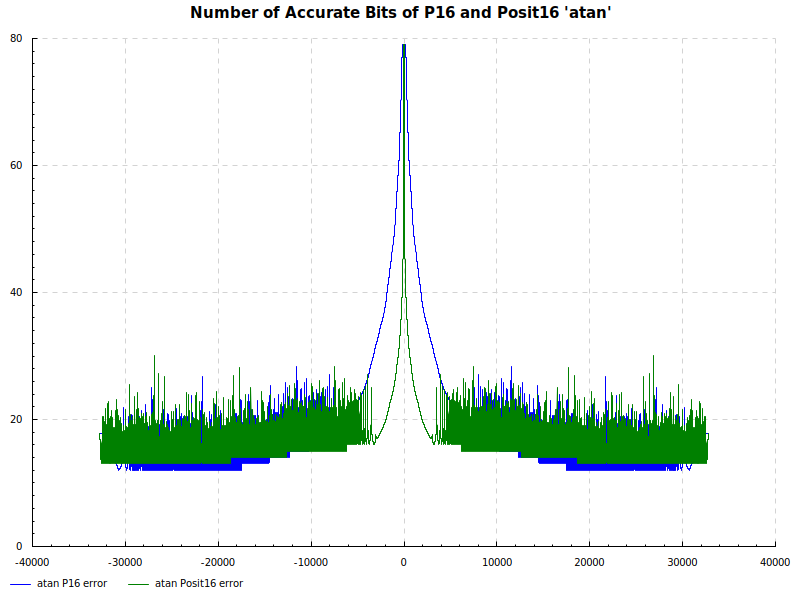

Number of Accurate Bits sinh: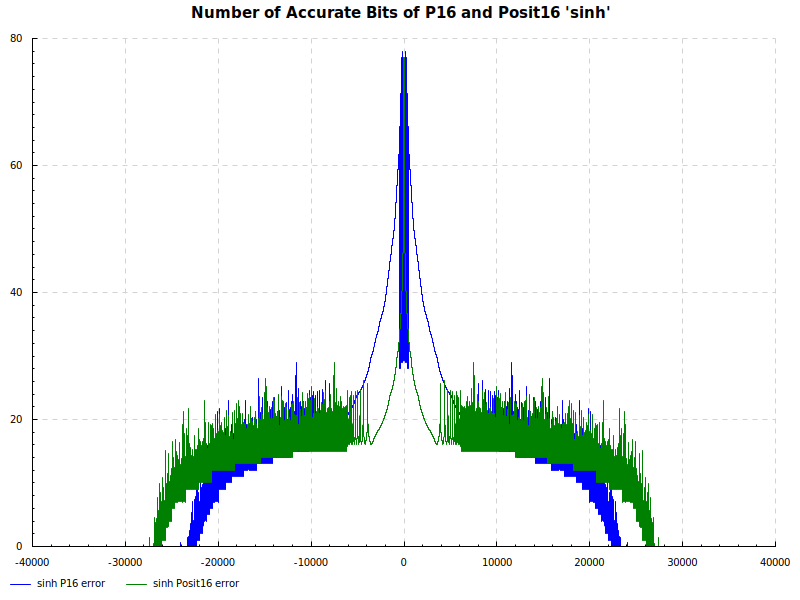

Number of Accurate Bits cosh: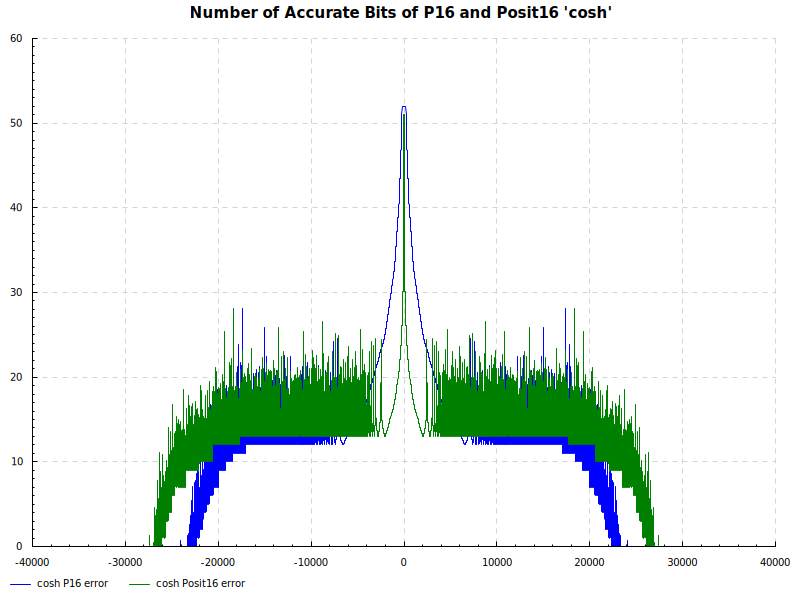

Number of Accurate Bits asinh: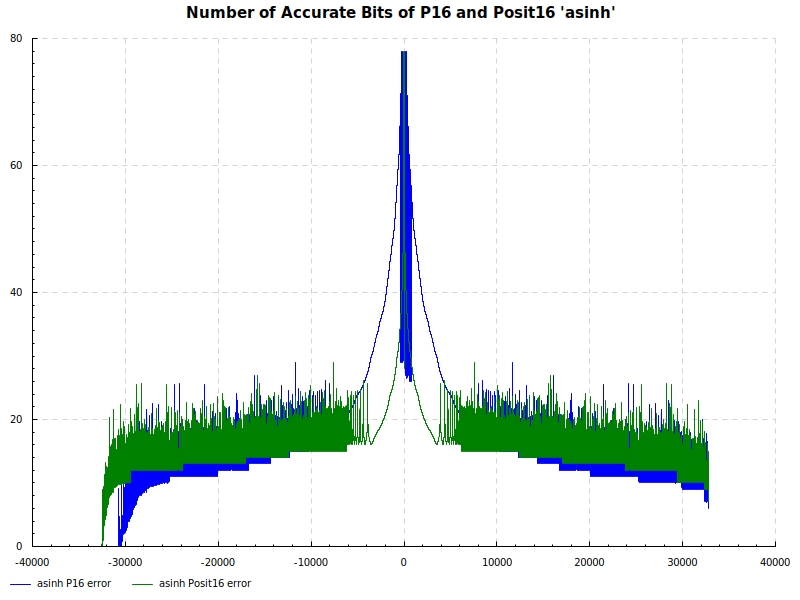

Number of Accurate Bits acosh: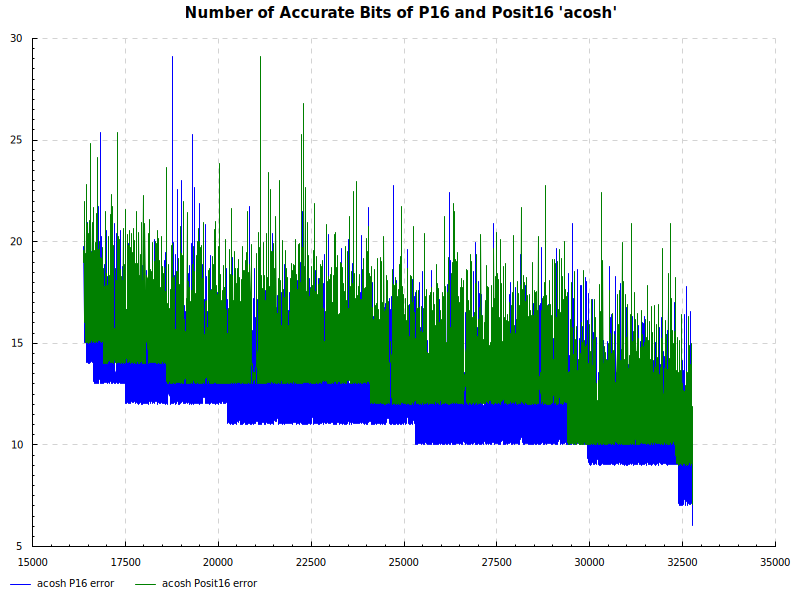

Number of Accurate Bits atanh: