Tensors of statically known size.
This library provides a toolkit for working with tensors of statically known size and element's type. See README.md
Static tensor
Sometimes when working with vectors or matrices or tensors of any rank, you know their sizes and types of their elements at compile time, and you don't need to change them at runtime.
This library provides a uniform interface for working with tensors of any rank. It uses type-level programing to catch errors at compile time instead of runtime. It also (ab)uses GHC optimizations to unroll loops to achieve greater performance.
Tensor data family
The library is built around a data family of tensors
-- | Data family of unboxed tensors. Dimensions of a tensor are represented as type-level list of
-- naturals. For instance, @Tensor [3] Float@ is a vector of 3 'Float' elements; @Tensor [4,3] Double@
-- is a matrix with 4 rows 3 columns of 'Double' and so on.
class IsTensor (dims :: [Nat]) e where
{-# MINIMAL tensor, unsafeFromList, toList #-}
-- | Tensor data constructor for given size and element type.
data Tensor dims e :: Type
-- | Alias for a concrete tensor data constructor.
--
-- >>> tensor @[2,2] @Int 0 1 2 3
-- Tensor'2'2 [[0,1],[2,3]]
tensor :: TensorConstructor dims e
-- | Build tensor from the list. The list must contain at least 'length' elements or method will throw an exception.
unsafeFromList :: [e] -> Tensor dims e
-- | Convert tensor to list.
toList :: Tensor dims e -> [] e
In order to start to work with the library, you need to create instances of this data family with desired sizes and element's types. For this, you can use Template Haskell functions
Data.Tensor.Static.TH.genTensorInstance :: NonEmpty Int -- ^ Dimensions of the tensor.
-> Name -- ^ Type of elements.
-> Q [Dec]
Data.Vector.Static.genVectorInstance :: Int -- ^ Size of the vector.
-> Name -- ^ Type of elements.
-> Q [Dec]
Data.Matrix.Static.genMatrixInstance :: Int -- ^ Number of rows.
-> Int -- ^ Number of columns.
-> Name -- ^ Type of elements.
-> Q [Dec]
This code, for example
$(genVectorInstance 4 ''Float)
$(genMatrixInstance 4 4 ''Float)
$(genTensorInstance [2, 3, 4] ''Float)
will generate:
- data instance for vector of 4 elements of type
Float - data instance for matrix of 4 rows and 4 columns of type
Float - data instance for tensor with dimensions 2x3x4 of type
Float
Now you can create a value of a tensor with functions vector, matrix, tensor which are just aliases for concrete generated data constructors.
{-# LANGUAGE TypeApplications #-}
v :: Vector 4 Float
v = vector @4 @Float 0 1 2 3
m :: Matrix 4 4 Float
m = matrix @4 @4 @Float 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
t :: Tensor '[2, 3, 4] Float
t = tensor @'[2, 3, 4] @Float 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
You can add tensors of the same size:
v2 = v `add` v
m2 = m `add` m
You can multiply matrix of size m*n by matrix of size n*o to get matrix of size m*o:
$(genMatrixInstance 3 3 ''Float)
$(genMatrixInstance 3 4 ''Float)
$(genMatrixInstance 4 3 ''Float)
m1 :: Matrix 3 4 Float
m1 = matrix @3 @4 @Float 0 1 2 3 4 5 6 7 8 9 10 11
m2 :: Matrix 4 3 Float
m2 = matrix @4 @3 @Float 0 1 2 3 4 5 6 7 8 9 10 11
mm :: Matrix 3 3 Float
mm = m1 `mult` m2
You can multiply matrix of size m*n by vector of size n:
mv :: Vector 4 Float
mv = m `mult` v
vm :: Vector 4 Float
vm = v `mult` m
In all those examples, if the dimensions of the tensors have been incompatible, you would have received a compilation error.
Loop unrolling
The library (ab)uses GHC optimizations to unroll loops to achieve greater performance.
For example, matrix multiplication function specialized to concrete size and type
mm :: Matrix 3 3 Float -> Matrix 3 3 Float -> Matrix 3 3 Float
mm = mult
is compiled to this nice Core
Mm.mm1
:: Data.Tensor.Static.Tensor '[3, 3] Float
-> Data.Tensor.Static.Tensor '[3, 3] Float
-> Data.Tensor.Static.Tensor (MatrixMultDims '[3, 3] '[3, 3]) Float
Mm.mm1
= \ (m0 :: Data.Tensor.Static.Tensor '[3, 3] Float)
(m1 :: Data.Tensor.Static.Tensor '[3, 3] Float) ->
case m0 `cast` <Co:1> of
{ Tensor'3'3'Float dt dt1 dt2 dt3 dt4 dt5 dt6 dt7 dt8 ->
case m1 `cast` <Co:1> of
{ Tensor'3'3'Float dt9 dt10 dt11 dt12 dt13 dt14 dt15 dt16 dt17 ->
(Mm.Tensor'3'3'Float
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt dt9)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt1 dt12) (GHC.Prim.timesFloat# dt2 dt15)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt dt10)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt1 dt13) (GHC.Prim.timesFloat# dt2 dt16)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt dt11)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt1 dt14) (GHC.Prim.timesFloat# dt2 dt17)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt3 dt9)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt4 dt12) (GHC.Prim.timesFloat# dt5 dt15)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt3 dt10)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt4 dt13) (GHC.Prim.timesFloat# dt5 dt16)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt3 dt11)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt4 dt14) (GHC.Prim.timesFloat# dt5 dt17)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt6 dt9)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt7 dt12) (GHC.Prim.timesFloat# dt8 dt15)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt6 dt10)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt7 dt13) (GHC.Prim.timesFloat# dt8 dt16)))
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt6 dt11)
(GHC.Prim.plusFloat#
(GHC.Prim.timesFloat# dt7 dt14) (GHC.Prim.timesFloat# dt8 dt17))))
`cast` <Co:10>
}
}
For implementation details of this trick see Data.List.Unrolled module. Also see test suite for more Core dumps.
Performance
Loop unrolling allows to achive greater performance. In matrix multiplication benchmark, for instance, this library is 3 times faster than the linear package. 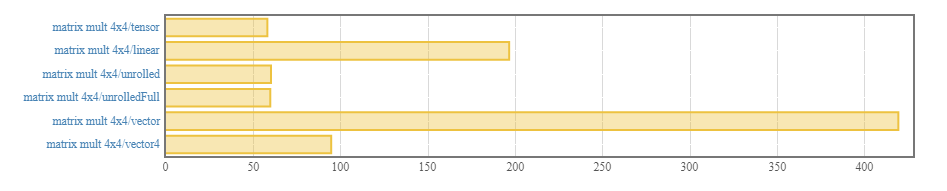
benchmarking matrix mult 4x4/tensor
time 58.24 ns (58.13 ns .. 58.39 ns)
1.000 R² (1.000 R² .. 1.000 R²)
mean 58.16 ns (58.03 ns .. 58.41 ns)
std dev 557.6 ps (304.1 ps .. 904.9 ps)
benchmarking matrix mult 4x4/linear
time 197.2 ns (196.3 ns .. 198.5 ns)
1.000 R² (0.999 R² .. 1.000 R²)
mean 197.3 ns (196.2 ns .. 198.8 ns)
std dev 4.364 ns (3.190 ns .. 5.935 ns)
variance introduced by outliers: 30% (moderately inflated)
benchmarking matrix mult 4x4/unrolled
time 60.11 ns (60.01 ns .. 60.25 ns)
1.000 R² (1.000 R² .. 1.000 R²)
mean 59.98 ns (59.88 ns .. 60.10 ns)
std dev 376.7 ps (320.8 ps .. 455.2 ps)
benchmarking matrix mult 4x4/unrolledFull
time 60.20 ns (59.85 ns .. 60.62 ns)
1.000 R² (1.000 R² .. 1.000 R²)
mean 59.89 ns (59.71 ns .. 60.14 ns)
std dev 691.5 ps (518.4 ps .. 949.5 ps)
variance introduced by outliers: 11% (moderately inflated)
benchmarking matrix mult 4x4/vector
time 420.1 ns (419.2 ns .. 420.9 ns)
1.000 R² (1.000 R² .. 1.000 R²)
mean 418.0 ns (416.9 ns .. 419.4 ns)
std dev 3.881 ns (2.799 ns .. 6.224 ns)
benchmarking matrix mult 4x4/vector4
time 95.30 ns (94.95 ns .. 95.59 ns)
1.000 R² (1.000 R² .. 1.000 R²)
mean 94.59 ns (94.35 ns .. 94.86 ns)
std dev 877.4 ps (721.2 ps .. 1.167 ns)
