Boundary Line Analysis.

BLA

Overview

The BLA R package provides a set of tools to fit boundary line models to a data set as proposed by Webb (1972). It includes a suite of methods which have been introduced since the original manually-drawn boundary lines were proposed. These include methods based on binning the independent variable, the BOLIDES algorithm of Schug et al. (1995), quantile regression and the statistically robust censored bivariate normal model of Milne et al. (2006). It also provides data exploration methods to check for outliers and to provide initial evidence for a limiting boundary in data sets as initial steps before doing boundary line analysis. It includes functions to determine suitable starting values for boundary line parameters for estimation by numerical optimization procedures. Learn more in vignette("Introduction_to_BLA").

How can I install the package?

Install the current version of the package from CRAN.

install.packages("BLA")

What can I use the BLA package for?

The classical situation in which BLA is used is to model the relationship between some response variable for a biological system (e.g. the yield of a crop) and a variable which is potentially limiting on that response (e.g. soil P concentration). The approach is suitable for large data sets from surveys i.e. cases in which multiple potential limiting factors occur but are not controlled experimentally. In the example of crop yield and soil P concentration, one can determine the largest expected yield for a given soil P concentration value, also called the boundary pH value. There are various methods to fit the boundary model in the BLA package, encoded in the functions blbin(), bolides(), blqr() and cbvn(). Additionally, the BLA provides function for initial data exploratory and post-hoc analysis.

The example below uses the censored bivariate normal model, cbvn(), function to fit the boundary line:

Load the package

library(BLA)
library(aplpack)

In addition to the BLA, the aplpack package is loaded which provides the bagplot() function for outlier detection.

Exploratory analysis

There are three important exploratory steps required prior to fitting boundary line models when using cbvn(). These include (1) checking the distribution of the potential limiting and response variables to access if they fulfill the assumption of normality, (2) detection of outliers, and (3) the determination of evidence of boundary existence in a dataset.

1. Testing for normality

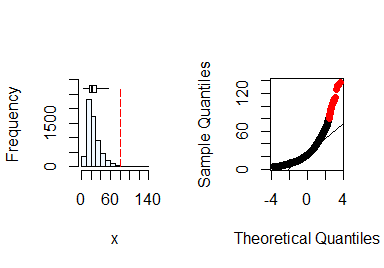
The function summastat() can be used for this purpose. Starting with soil P concentration:

x <- soil$P 
summastat(x)

#>         Mean Median Quartile.1 Quartile.3 Variance       SD Skewness
#> [1,] 25.9647     22         16         32 207.0066 14.38772 1.840844
#>      Octile skewness Kurtosis No. outliers
#> [1,]       0.3571429 5.765138           43

From the plots and the summary statistics, the x variable can not be assumed to be from a normal distribution and hence requires transformation to fulfill the assumption of normality. You can do this by taking the natural log of x.

summastat(log(x))

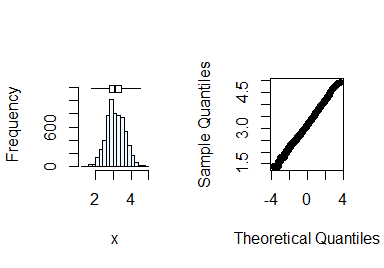
#>          Mean   Median Quartile.1 Quartile.3  Variance        SD  Skewness
#> [1,] 3.126361 3.091042   2.772589   3.465736 0.2556936 0.5056615 0.1297406
#>      Octile skewness    Kurtosis No. outliers
#> [1,]      0.08395839 -0.05372586            0

Normality can now be assumed after transformation. Next, you check the variable yield.

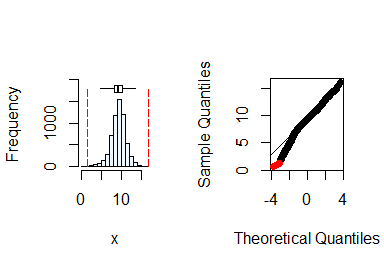
y <- soil$yield

summastat(y)

#>          Mean  Median Quartile.1 Quartile.3 Variance       SD   Skewness
#> [1,] 9.254813 9.36468   8.203703   10.39477 3.456026 1.859039 -0.4819805
#>      Octile skewness Kurtosis No. outliers
#> [1,]     -0.05793291 1.292635            7

From the plots and the summary statistics, the variable y can be assumed to be from a normal distribution.

2. Outlier identification and removal

This is done using the bagplot() function from the aplpack package. Its input is a matrix and hence we assign the x and y variables to a matrix data_ur.

  nobs<-length(soil$P) 
  data_ur<-matrix(NA,nobs,2)#  create a matrix: bagplot inputs data as a matrix
  data_ur[,1]<-log(soil$P) 
  data_ur[,2]<-soil$yield

  bag<-bagplot(data_ur,create.plot = F ) # bagplot identifies outliers

  data<-rbind(bag$pxy.bag,bag$pxy.outer) # new excludes bivariate outliers

3. Evidence of boundary presence

This is done using the function expl_boundary()

  x <- data[,1]
  y <- data[,2]

  expl_boundary(x,y,10,1000)
#> Note: This function may take a few minutes to run for large datasets.

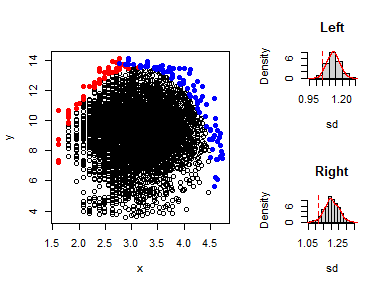
#>     Index Section    value
#> 1      sd    Left 1.045711
#> 2      sd   Right 1.115379
#> 3 Mean sd    Left 1.129992
#> 4 Mean sd   Right 1.204543
#> 5 p_value    Left 0.041000
#> 6 p_value   Right 0.029000

The p-values in the left and right sections are less than 0.05, indicating evidence of boundary existence. This justifies the fitting of a boundary line model to the dataset.

Boundary model fitting

Based on the structure of the data at the upper edge, a trapezium model can be fitted. Take note that any other model of your choice that is biologically plausible can be fitted. Below is an example of how you can use the cbvn() function to fit the boundary line.

It arguments include (1) a dataframe,data, containing the x and y variables, (2) a vector of initial start values for the optimization that includes the parameters of the boundary model and for the distribution (i.e. mean(x), mean(y), sd(x), sd(y) and cor(x,y)), and (3) the measurement error value, sigh, for the response variable. The rest of the inputs are related to the plot features as in the function plot() from base R.

The start values for the preferred model can be determined using the startValues() function. Set the argument model to the desired model e.g. model="trapezium", run the function and click on the plot of y against x, the points that make up the structure of the model at the upper edges of the data scatter.

plot(data)

startValues("trapezium")

Using the obtained values for the model, create a vector of start values.

data<-data.frame(x,y) 
start<-c(4,3,13.6, 35,-5,3,9,0.50,1.9,0.05) # initial start values for optimization

model <- cbvn(data, start = start, model = "trapezium", sigh=0.7, 
                 xlab = expression("Soil P"), ylab = expression("Yield/ t ha"^-1), 
                 pch = 16, plot = TRUE, col = "grey40", cex = 0.6)

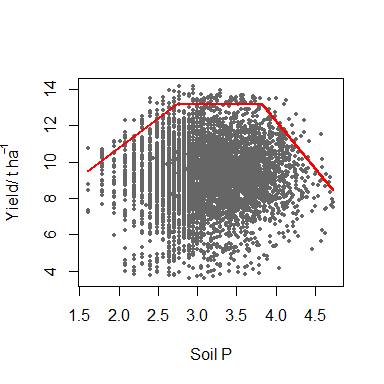
model
#> $Model
#> [1] "trapezium"
#> 
#> $Equation
#> [1] y = min (β₁ + β₂x, β₀, β₃ + β₄x)
#> 
#> $Parameters
#>          Estimate Standard error
#> β₁     4.29795522    1.035391840
#> β₂     3.23397375    0.460850826
#> β₀    13.15187257    0.206656034
#> β₃    33.17267393    1.693458789
#> β₄    -5.22857503    0.393758941
#> mux    3.12597270    0.006451086
#> muy    9.30482617    0.022879293
#> sdx    0.50053107    0.004561474
#> sdy    1.60754420    0.018448808
#> rcorr  0.04150832    0.014806076
#> 
#> $AIC
#>             
#> mvn 32429.55
#> BL  32391.07

The output gives the name of model fitted which is a “trapezium” in the case, its equation form, its parameters (the first 5 rows of the Parameters) and corresponding standard errors, and the AIC values for the boundary model, BL, and a corresponding multivariate normal model, mvn. Since the AIC for the BL is smaller than mvn, the boundary line model is appropriate.

Predicting boundary yield and critical soil P value

The boundary yield given the soil P concentration for each data point can be predicted using the function predictBL() :

P_values <- log(soil$P)
P_values[is.na(x)] <- mean(x, na.rm = TRUE) # replace missing values with mean pH
predicted_yield <- predictBL(model, P_values)


head(predicted_yield) # predicted yield for the first six farms
#> [1] 11.74445 11.40372 11.74445 11.40372 11.40372 12.33408

The critical P value is the point beyond which yield increase is not expected. You can calculate it from the model parameters as follows:

intercept <- model$Parameters[1]
slope <- model$Parameters[2]
plateau <- model$Parameters[3]

critical_P <- (plateau - intercept) / slope

print(exp(critical_P))# results are in mg/l
#> [1] 15.45268

Other boundary line post-hoc analysis procedures can be conducted. For more information, See vignette("Censored_bivariate_normal_model") and vignette("Introduction_to_BLA").

References

1. Milne, A. E., Wheeler, H. C., & Lark, R. M. (2006). On testing biological data for the presence of a boundary. Annals of Applied Biology, 149 , 213-222. https://doi.org/10.1111/j.1744-7348.2006.00085.x

2. Schnug, E., Heym, J. M., & Murphy, D. P. L. (1995). Boundary line determination technique (bolides). In P. C. Robert, R. H. Rust, & W. E. Larson (Eds.), site specific management for agricultural systems (p. 899-908). Wiley Online Library. https://doi.org/10.2134/1995.site-specificmanagement.c66

3. Webb, R. A. (1972). Use of the boundary line in analysis of biological data. Journal of Horticultural Science, 47, 309–319. https://doi.org/10.1080/00221589.1972.11514472