Plot Positive and Negative Predictive Values for Medical Tests.

Bayesian reasoning

Bayesian reasoning in medical contexts

This package includes a few functions to plot and help understand Positive and Negative Predictive Values, and their relationship with Sensitivity, Specificity and Prevalence.

• The Positive Predictive Value of a medical test is the probability that a positive result will mean having the disease. Formally p(Disease|+)
• The Negative Predictive Value of a medical test is the probability that a negative result will mean not having the disease. Formally p(Healthy|-)

The BayesianReasoning package has three main functions:

• PPV_heatmap(): Plot heatmaps with PPV or NPV values for the given test and disease parameters.
• PPV_diagnostic_vs_screening(): Plots the difference between the PPV of a test in a diagnostic context (very high prevalence; or a common study sample, e.g. ~50% prevalence) versus a screening context (lower prevalence).
• min_possible_prevalence(): Calculates how high should the prevalence of a disease be to reach a desired PPV given certain test parameters.

If you want to install the package can use: remotes::install_github("gorkang/BayesianReasoning"). Please report any problems you find in the Issues Github page.

There is a shiny app implementation with most of the main features available.

PPV_heatmap()

Plot heatmaps with PPV or NPV values for a given specificity and a range of Prevalences and FP or FN (1 - Sensitivity). The basic parameters are:

• min_Prevalence: Min prevalence in y axis. “min_Prevalence out of y”
• max_Prevalence: Max prevalence in y axis. “1 out of max_Prevalence”
• Sensitivity: Sensitivity of the test
• max_FP: FP is 1 - specificity. The x axis will go from FP = 0% to max_FP
• Language: “es” for Spanish or “en” for English

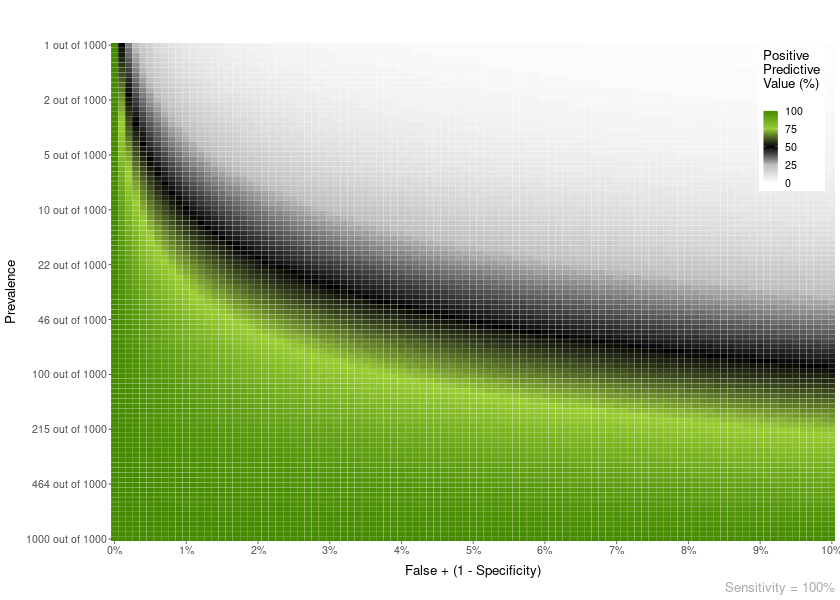
PPV_heatmap(min_Prevalence = 1,
            max_Prevalence = 1000, 
            Sensitivity = 100, limits_Specificity = c(90, 100),
            Language = "en")

NPV

You can also plot an NPV heatmap with PPV_NPV = “NPV”.

PPV_heatmap(PPV_NPV = "NPV",
            min_Prevalence = 800, max_Prevalence = 1000, 
            Specificity = 95, limits_Sensitivity = c(90, 100),
            Language = "en")

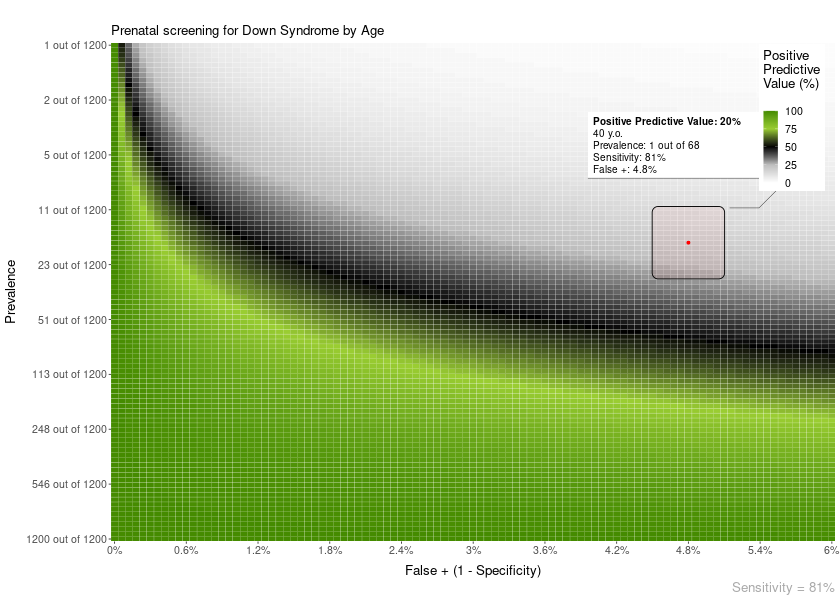
Area overlay

You can add different types of overlay to the plots.

For example, an area overlay showing the point PPV for a given prevalence and FP or FN:

PPV_heatmap(min_Prevalence = 1, max_Prevalence = 1200, 
            Sensitivity = 81, 
            limits_Specificity = c(94, 100),
            label_subtitle = "Prenatal screening for Down Syndrome by Age",
            overlay = "area",
            overlay_labels = "40 y.o.",
            overlay_position_FP = 4.8,
            overlay_prevalence_1 = 1,
            overlay_prevalence_2 = 68)

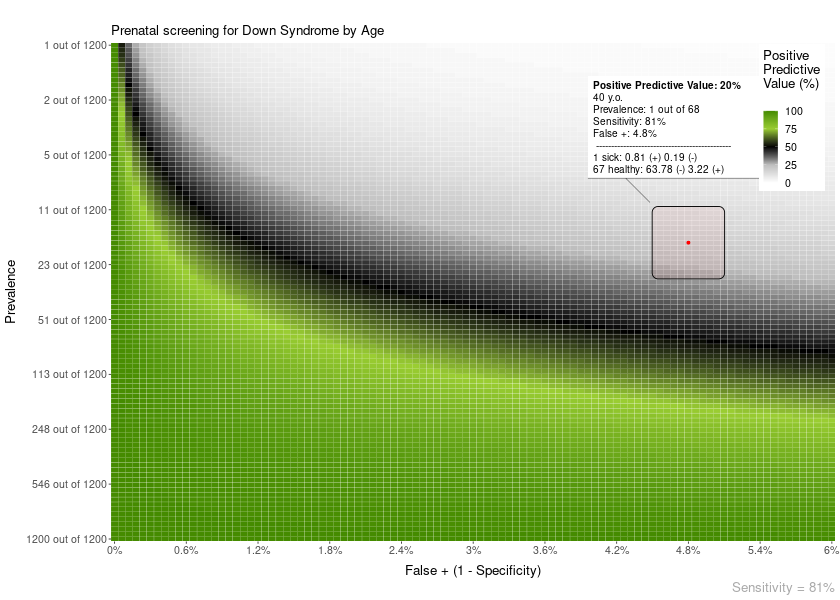
The area plot overlay can show more details about how the calculation of PPV/NPV is performed:

PPV_heatmap(min_Prevalence = 1, max_Prevalence = 1200, 
            Sensitivity = 81, 
            limits_Specificity = c(94, 100),
            label_subtitle = "Prenatal screening for Down Syndrome by Age", 
            overlay_extra_info = TRUE,
            overlay = "area",
            overlay_labels = "40 y.o.",
            overlay_position_FP = 4.8,
            overlay_prevalence_1 = 1,
            overlay_prevalence_2 = 68)

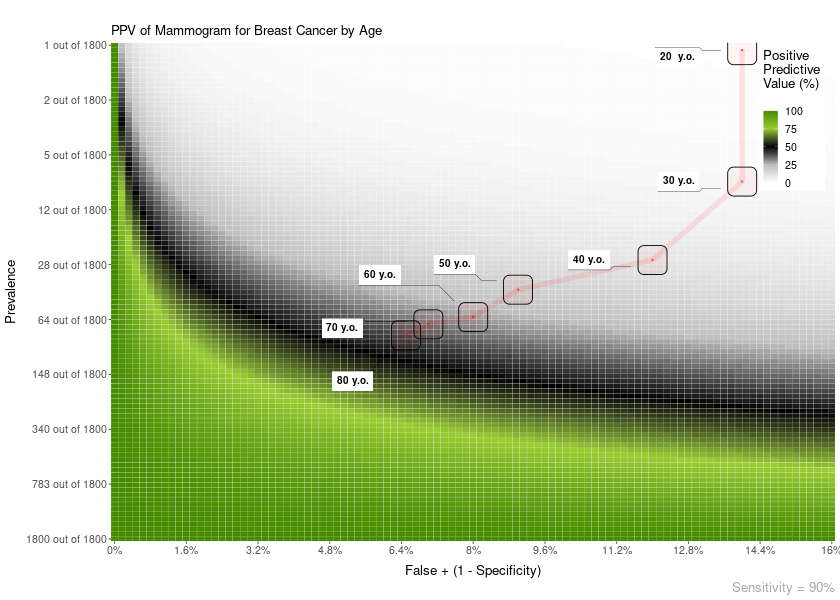
Line overlay

Also, you can add a line overlay highlighting a range of prevalences and FP. This is useful, for example, to show how the PPV of a test changes with age:

PPV_heatmap(min_Prevalence = 1, max_Prevalence = 1800, 
            Sensitivity = 90, 
            limits_Specificity = c(84, 100),
            label_subtitle = "PPV of Mammogram for Breast Cancer by Age",
            overlay = "line", 
            overlay_labels = c("80 y.o.", "70 y.o.", "60 y.o.", "50 y.o.", "40 y.o.", "30 y.o.", "20  y.o."),
            overlay_position_FP = c(6.5, 7, 8, 9, 12, 14, 14),
            overlay_prevalence_1 = c(1, 1, 1, 1, 1, 1, 1),
            overlay_prevalence_2 = c(22, 26, 29, 44, 69, 227, 1667))

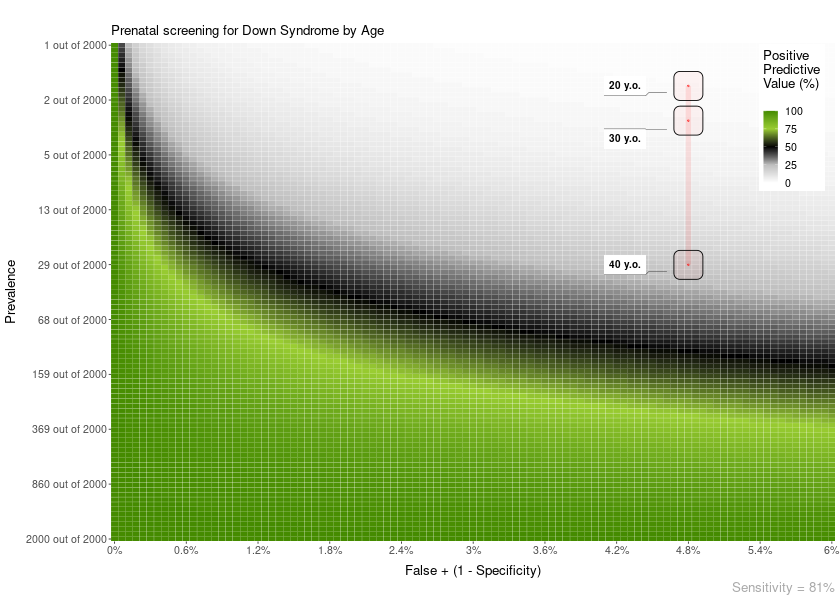
Another example. In this case, the FP is constant across age:

PPV_heatmap(min_Prevalence = 1, max_Prevalence = 2000, Sensitivity = 81, 
            limits_Specificity = c(94, 100),
            label_subtitle = "Prenatal screening for Down Syndrome by Age",
            overlay = "line",
            overlay_labels = c("40 y.o.", "30 y.o.", "20 y.o."),
            overlay_position_FP = c(4.8, 4.8, 4.8),
            overlay_prevalence_1 = c(1, 1, 1),
            overlay_prevalence_2 = c(68, 626, 1068))

PPV_diagnostic_vs_screening()

In scientific studies developing a new test for the early detection of a medical condition, it is quite common to use a sample where 50% of participants has a medical condition and the other 50% are normal controls. This has the unintended effect of maximizing the PPV of the test.

This function shows a plot with the difference between the PPV of a diagnostic context (very high prevalence; or a common study sample, e.g. ~50% prevalence) versus that of a screening context (lower prevalence).

PPV_diagnostic_vs_screening(max_FP = 10, 
                            Sensitivity = 100, 
                            prevalence_screening_group = 1000, 
                            prevalence_diagnostic_group = 2)

min_possible_prevalence()

Imagine you would like to use a test in a population and want to have a 98% PPV. That is, IF a positive result comes out in the test, you would like a 98% certainty that it is a true positive.

How high should the prevalence of the disease be in that group?

min_possible_prevalence(Sensitivity = 100, 
                        FP_test = 0.1, 
                        min_PPV_desired = 98)

To reach a PPV of 98 when using a test with 100 % Sensitivity and 0.1 % False Positive Rate, you need a prevalence of at least 1 out of 21

Another example, with a very good test, and lower expectations:

min_possible_prevalence(Sensitivity = 99.9, 
                        FP_test = .1, 
                        min_PPV_desired = 70)

To reach a PPV of 70 when using a test with 99.9 % Sensitivity and 0.1 % False Positive Rate, you need a prevalence of at least 1 out of 429

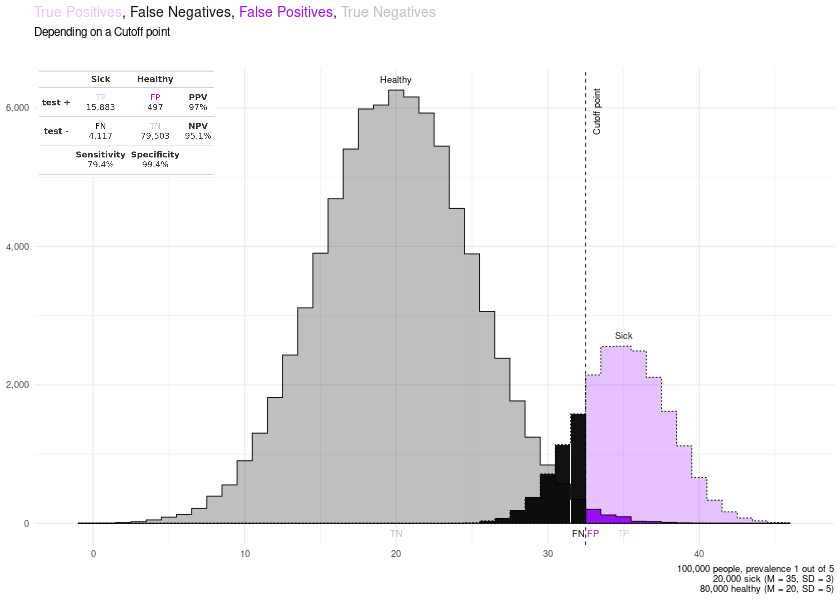
plot_cutoff()

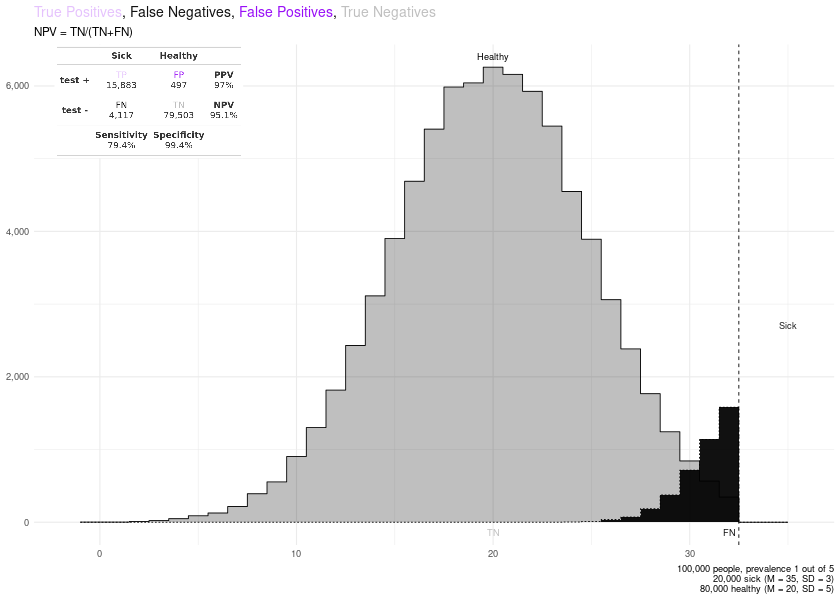
Since v0.4.2 you can also plot the distributions of sick and healthy individuals and learn about how a cutoff point changes the True Positives, False Positives, True Negatives, False Negatives, Sensitivity, Specificity, PPV and NPV.

PLOTS = plot_cutoff(prevalence = 0.2,
                    cutoff_point = 33, 
                    mean_sick = 35, 
                    mean_healthy = 20, 
                    sd_sick = 3, 
                    sd_healthy = 5
                    )

PLOTS$final_plot

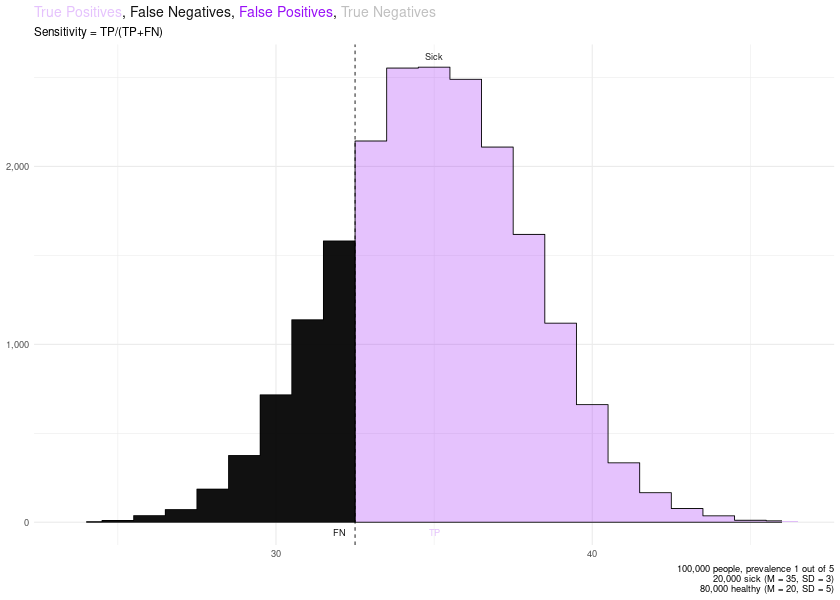
Then, with remove_layers_cutoff_plot() you can remove specific layers, to help you understand some of these concepts.

# Sensitivity
remove_layers_cutoff_plot(PLOTS$final_plot, delete_what = c("FP", "TN")) + ggplot2::labs(subtitle = "Sensitivity = TP/(TP+FN)")

# Specificity
remove_layers_cutoff_plot(PLOTS$final_plot, delete_what = c("FN", "TP")) + ggplot2::labs(subtitle = "Specificity = TN/(TN+FP)")

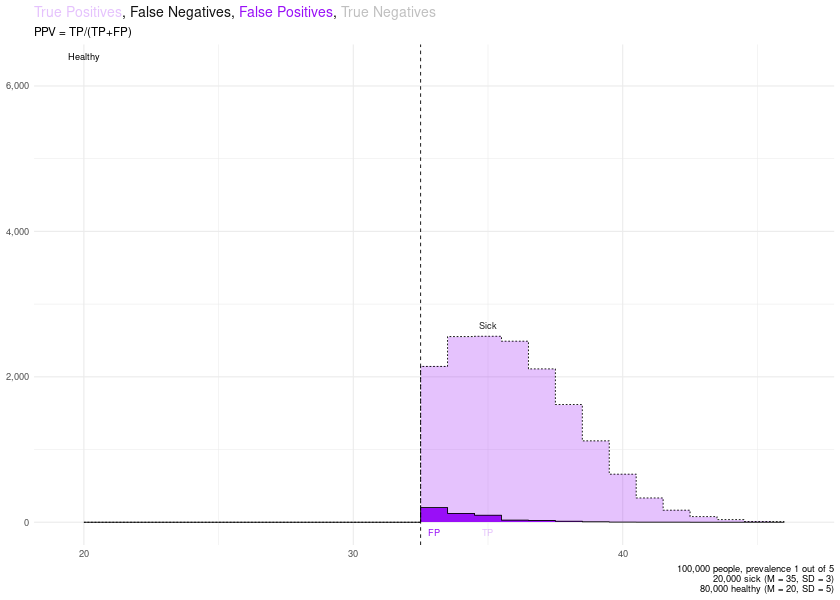
# PPV
remove_layers_cutoff_plot(PLOTS$final_plot, delete_what = c("TN", "FN")) + ggplot2::labs(subtitle = "PPV = TP/(TP+FP)")

# NPV
remove_layers_cutoff_plot(PLOTS$final_plot, delete_what = c("TP", "FP")) + ggplot2::labs(subtitle = "NPV = TN/(TN+FN)")