Description

Computation of 2D and 3D Elliptical Joint Confidence Regions.

Description

Computing elliptical joint confidence regions at a specified confidence level. It provides the flexibility to estimate either classical or robust confidence regions, which can be visualized in 2D or 3D plots. The classical approach assumes normality and uses the mean and covariance matrix to define the confidence regions. Alternatively, the robustified version employs estimators like minimum covariance determinant (MCD) and M-estimator, making them less sensitive to outliers and departures from normality. Furthermore, the functions allow users to group the dataset based on categorical variables and estimate separate confidence regions for each group. This capability is particularly useful for exploring potential differences or similarities across subgroups within a dataset. Varmuza and Filzmoser (2009, ISBN:978-1-4200-5947-2). Johnson and Wichern (2007, ISBN:0-13-187715-1). Raymaekers and Rousseeuw (2019) <DOI:10.1080/00401706.2019.1677270>.

README.md

cran.r-project.org

ConfidenceEllipse

The ConfidenceEllipse package computes the coordinate points of confidence ellipses and ellipsoids for a given bivariate and trivariate dataset. The size of the ellipse and ellipsoid is determined by the confidence level, and the shape is determined by the covariance matrix. The confidence level is usually chosen to be 95% or 99%, and the resulting confidence region contains the points that are expected to lie within the multivariate distribution.

Installation

You can install the development version of ConfidenceEllipse like so:

# install.packages("remotes")
# remotes::install_github("ChristianGoueguel/ConfidenceEllipse")

Example

library(magrittr)
library(tidyselect)
library(patchwork)
library(dplyr)
library(ggplot2)
library(purrr)
library(tidyr)

library(ConfidenceEllipse)

Dataset

The dataset is comprised of 13 different measurements for 180 archaeological glass vessels from different groups (Janssen, K.H.A., De Raedt, I., Schalm, O., Veeckman, J.: Microchim. Acta 15 (suppl.) (1998) 253-267. Compositions of 15th - 17th century archaeological glass vessels excavated in Antwerp.)

data("glass", package = "ConfidenceEllipse")

glass %>% glimpse()
#> Rows: 180
#> Columns: 14
#> $ glassType <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, …
#> $ Na2O      <dbl> 13.904, 14.194, 14.668, 14.800, 14.078, 13.600, 12.942, 15.6…
#> $ MgO       <dbl> 2.244, 2.184, 3.034, 2.455, 2.480, 1.648, 2.690, 2.028, 2.25…
#> $ Al2O3     <dbl> 1.312, 1.310, 1.362, 1.385, 1.072, 2.012, 1.420, 1.242, 1.07…
#> $ SiO2      <dbl> 67.752, 67.076, 63.254, 63.790, 68.768, 69.628, 64.012, 70.6…
#> $ P2O5      <dbl> 0.884, 0.938, 0.988, 1.200, 0.682, 0.698, 0.966, 0.210, 0.75…
#> $ SO3       <dbl> 0.052, 0.024, 0.064, 0.115, 0.070, 0.038, 0.046, 0.310, 0.03…
#> $ Cl2O      <dbl> 0.936, 0.966, 0.886, 0.988, 0.966, 0.908, 0.896, 0.676, 0.93…
#> $ K2O       <dbl> 3.044, 3.396, 2.828, 2.878, 2.402, 3.196, 2.526, 2.326, 2.32…
#> $ CaO       <dbl> 8.784, 8.636, 11.088, 10.833, 8.808, 6.160, 12.982, 6.324, 9…
#> $ MnO       <dbl> 0.674, 0.698, 1.240, 0.978, 0.310, 1.170, 0.874, 0.214, 0.60…
#> $ Fe2O3     <dbl> 0.364, 0.336, 0.400, 0.433, 0.242, 0.650, 0.516, 0.278, 0.25…
#> $ BaO       <dbl> 0.040, 0.040, 0.046, 0.025, 0.022, 0.156, 0.014, 0.032, 0.02…
#> $ PbO       <dbl> 0.004, 0.198, 0.134, 0.120, 0.102, 0.136, 0.120, 0.062, 0.02…

Confidence Region

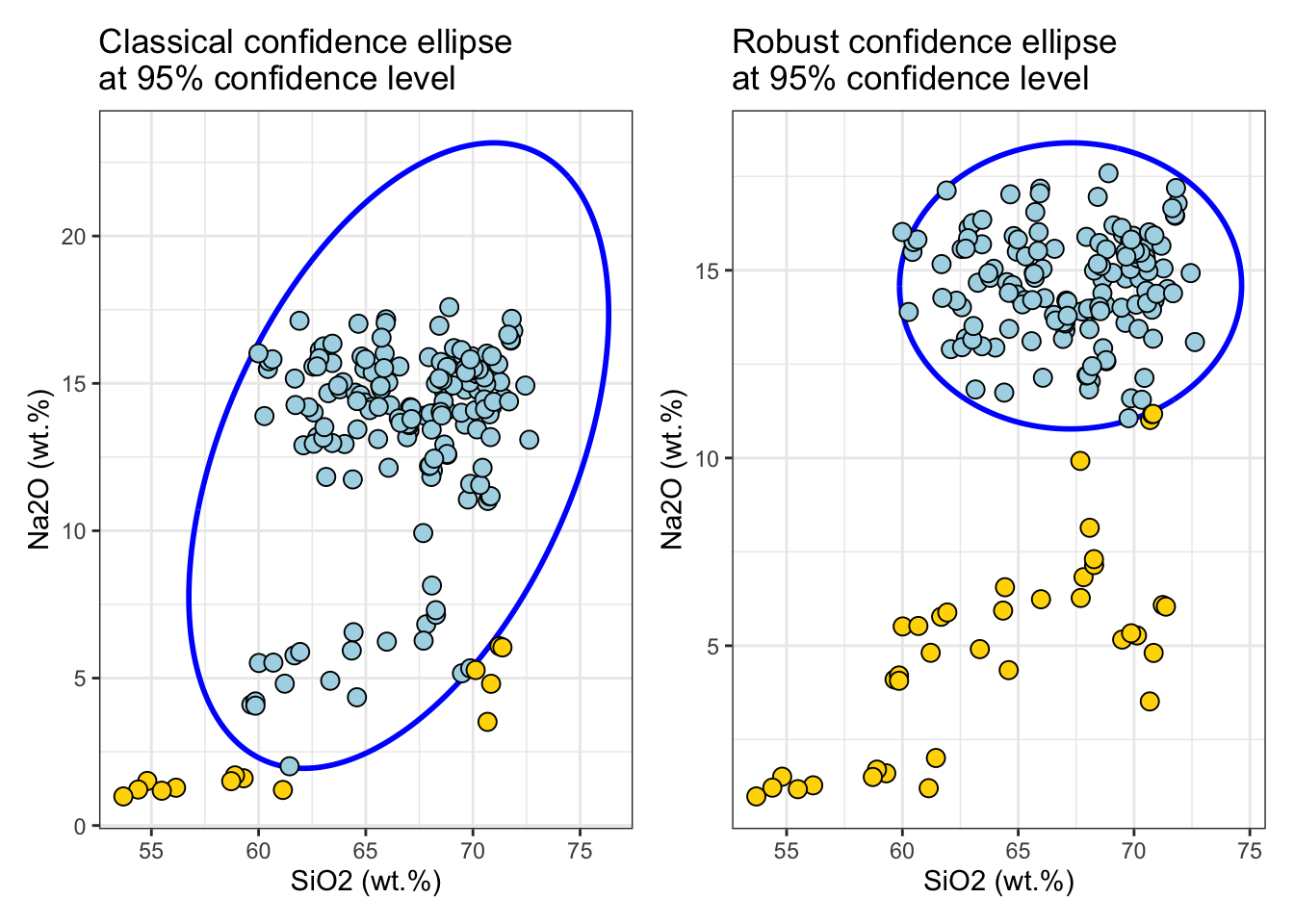
Classical and robust confidence ellipse

First, the confidence_ellipse function is used to compute coordinate points of the confidence ellipse and then the ellipse is plotted on a two-dimensional plot x and y of the data. Points that lie outside the ellipse are considered to be outliers, while points that lie within the ellipse are considered to be part of the underlying distribution with the specified confidence level conf_level.

ellipse_95 <- confidence_ellipse(glass, x = SiO2, y = Na2O, conf_level = 0.95)
rob_ellipse_95 <- confidence_ellipse(glass, x = SiO2, y = Na2O, conf_level = 0.95, robust = TRUE)

ellipse_95 %>% glimpse()
#> Rows: 361
#> Columns: 2
#> $ x <dbl> 74.45896, 74.35724, 74.25314, 74.14669, 74.03792, 73.92686, 73.81356…
#> $ y <dbl> 21.99964, 22.08244, 22.16235, 22.23932, 22.31335, 22.38440, 22.45245…

cutoff <- qchisq(0.95, df = 2)
 MDsquared <- glass %>%
  select(SiO2, Na2O) %>%
  as.matrix() %>%
  mahalanobis(colMeans(.), cov(.), inverted = FALSE)

plot1 <- 
  ggplot() +
  geom_path(data = ellipse_95, aes(x = x, y = y), color = "blue", linewidth = 1L) +
  geom_point(
    data = glass %>% 
      mutate(md = MDsquared) %>%
      filter(md <= cutoff),
    aes(x = SiO2, y = Na2O),
    shape = 21L, color = "black", fill = "lightblue", size = 3L) +
  geom_point(
    data = glass %>% 
      mutate(md = MDsquared) %>%
      filter(md > cutoff),
    aes(x = SiO2, y = Na2O),
    shape = 21L, color = "black", fill = "gold", size = 3L) +
  labs(
    x = "SiO2 (wt.%)", 
    y = "Na2O (wt.%)",
    title = "Classical confidence ellipse\nat 95% confidence level") +
  theme_bw() +
  theme(legend.position = "none")

x_mcd <- glass %>%
  select(SiO2, Na2O) %>%
  as.matrix() %>%
  robustbase::covMcd()

rob_MDsquared <- glass %>%
  select(SiO2, Na2O) %>%
  as.matrix() %>%
  mahalanobis(x_mcd$center, x_mcd$cov)

plot2 <- 
  ggplot() +
  geom_path(data = rob_ellipse_95, aes(x = x, y = y), color = "blue", linewidth = 1L) +
  geom_point(
    data = glass %>% 
      mutate(md = rob_MDsquared) %>%
      filter(md <= cutoff),
    aes(x = SiO2, y = Na2O),
    shape = 21L, color = "black", fill = "lightblue", size = 3L) +
  geom_point(
    data = glass %>% 
      mutate(md = rob_MDsquared) %>%
      filter(md > cutoff),
    aes(x = SiO2, y = Na2O),
    shape = 21L, color = "black", fill = "gold", size = 3L) +
  labs(
    x = "SiO2 (wt.%)", 
    y = "Na2O (wt.%)",
    title = "Robust confidence ellipse\nat 95% confidence level") +
  theme_bw() +
  theme(legend.position = "none")

plot1 | plot2

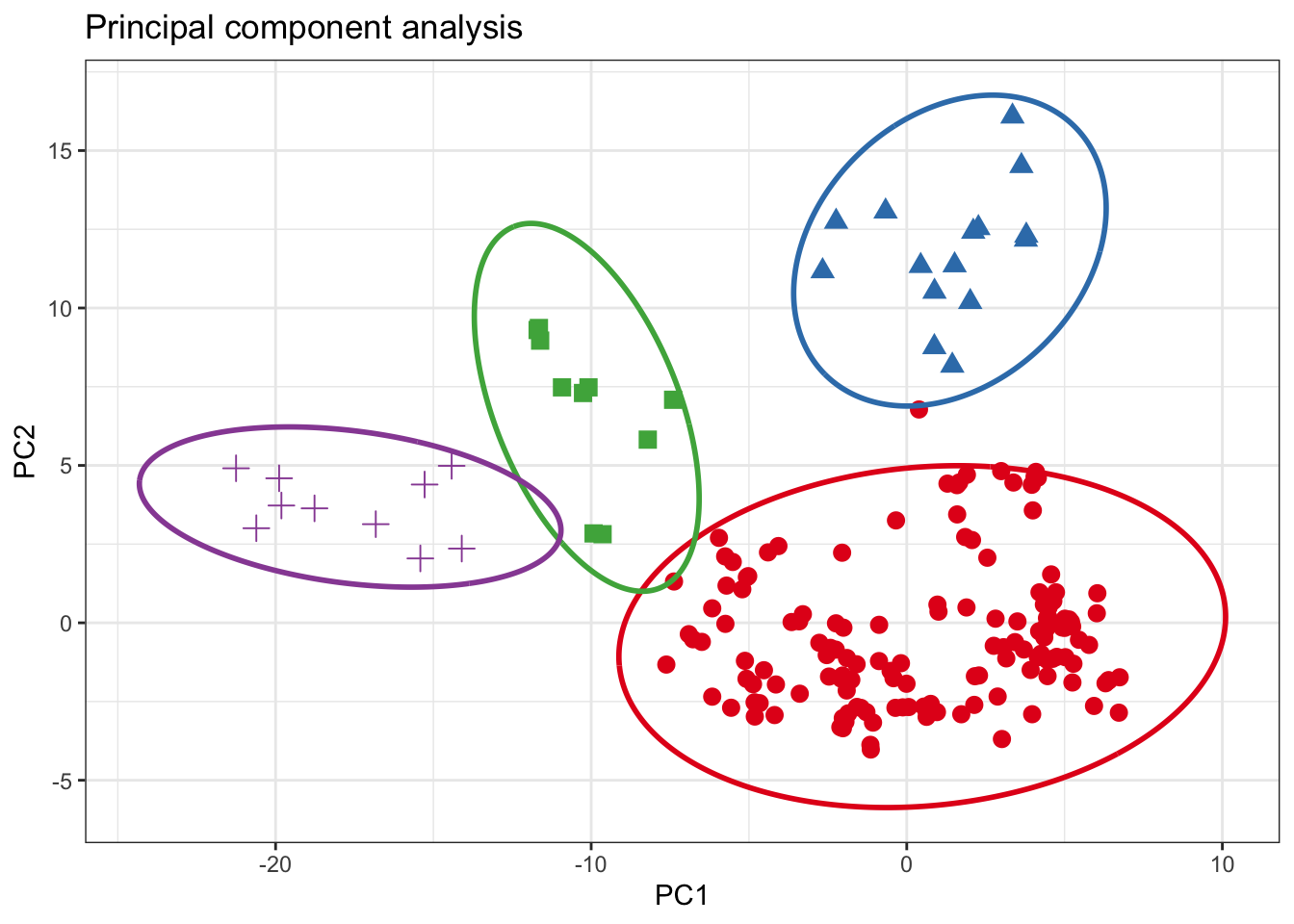
Grouping

For grouping bivariate data, the .group_by argument can be used if the data contains an unique grouping variable (.group_by = NULL by default). When a grouping variable is provided, the function will compute the ellipses separately for each level of the factor, allowing you to explore potential differences or patterns within subgroups of the data.

It’s important to note that the grouping variable should be appropriately coded as a factor before passing it to the .group_by argument. If the variable is currently stored as a character or numeric type, you may need to convert it to a factor using functions like as.factor() or forcats::as_factor().

rpca_scores <- glass %>%
  select(where(is.numeric) )%>% 
  pcaPP::PCAproj(method = "qn") %>%
  pluck("scores") %>%
  as_tibble() %>%
  mutate(glassType = glass %>% pull(glassType)) %>%
  rename(PC1 = Comp.1, PC2 = Comp.2)

ellipse_pca <- rpca_scores %>% confidence_ellipse(x = PC1, y = PC2, .group_by = glassType)

ggplot() +
  geom_point(data = rpca_scores, aes(x = PC1, y = PC2, color = glassType, shape = glassType), size = 3L) +
  geom_path(data = ellipse_pca, aes(x = x, y = y, color = glassType), linewidth = 1L) +
  scale_color_brewer(palette = "Set1", direction = 1) +
  labs(x = "PC1", y = "PC2", title = "Principal component analysis") +
  theme_bw() +
  theme(legend.position = "none")

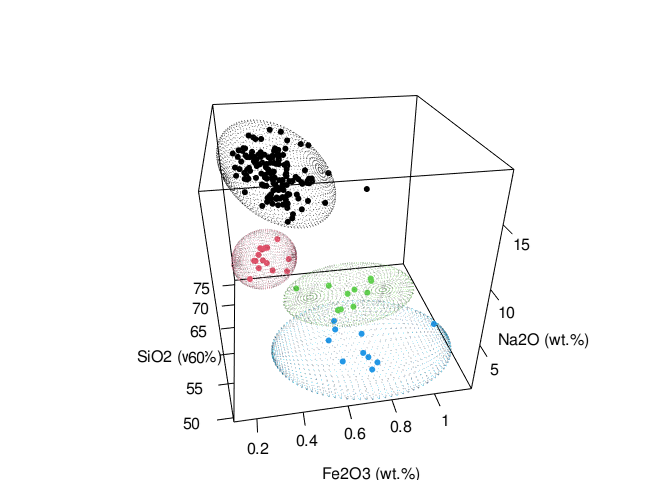
Ellipsoid

The confidence_ellipsoid function accepts an additional variable z and computes the ellipsoid for trivariate data.

ellipsoid_grp <- glass %>% confidence_ellipsoid(SiO2, Na2O, Fe2O3, glassType)

ellipsoid_grp %>% glimpse()
#> Rows: 10,000
#> Columns: 4
#> $ x         <dbl> 67.32486, 67.32486, 67.32486, 67.32486, 67.32486, 67.32486, …
#> $ y         <dbl> 14.51964, 14.51964, 14.51964, 14.51964, 14.51964, 14.51964, …
#> $ z         <dbl> 0.5971494, 0.5971494, 0.5971494, 0.5971494, 0.5971494, 0.597…
#> $ glassType <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …

rgl::setupKnitr(autoprint = TRUE)
rgl::plot3d(
  x = ellipsoid_grp$x, 
  y = ellipsoid_grp$y, 
  z = ellipsoid_grp$z,
  xlab = "SiO2 (wt.%)", 
  ylab = "Na2O (wt.%)", 
  zlab = "Fe2O3 (wt.%)",
  type = "s", 
  radius = 0.03,
  col = as.numeric(ellipsoid_grp$glassType)
  )
rgl::points3d(
  x = glass$SiO2, 
  y = glass$Na2O, 
  z = glass$Fe2O3, 
  col = as.numeric(glass$glassType),
  size = 5
  )
rgl::view3d(theta = 260, phi = 30, fov = 60, zoom = .85)

r-ConfidenceEllipse

ConfidenceEllipse

Installation

Example

Dataset

Confidence Region

Classical and robust confidence ellipse

Grouping

Ellipsoid

Version

License

Status

Source

Homepage

Platforms (77)

ConfidenceEllipse

Installation

Example

Dataset

Confidence Region

Classical and robust confidence ellipse

Grouping

Ellipsoid

Version

License

Status

Source

Homepage

Platforms77 (77)

Platforms (77)