Description

Diversity-Interactions (DI) Models.

Description

The 'DImodels' package is suitable for analysing data from biodiversity and ecosystem function studies using the Diversity-Interactions (DI) modelling approach introduced by Kirwan et al. (2009) <doi:10.1890/08-1684.1>. Suitable data will contain proportions for each species and a community-level response variable, and may also include additional factors, such as blocks or treatments. The package can perform data manipulation tasks, such as computing pairwise interactions (the DI_data() function), can perform an automated model selection process (the autoDI() function) and has the flexibility to fit a wide range of user-defined DI models (the DI() function).

README.md

cran.r-project.org

DImodels

The DImodels package is designed to make fitting Diversity-Interactions models easier. Diversity-Interactions (DI) models (Kirwan et al 2009) are a set of tools for analysing and interpreting data from experiments that explore the effects of species diversity (from a pool of S species) on community-level responses. Data suitable for DI models will include (at least) for each experimental unit: a response recorded at a point in time, and a set of proportions of S species $p_1$, $p_2$, …, $p_S$ from a point in time prior to the recording of the response. The proportions sum to 1 for each experimental unit.

Main changes in the package from version 1.3 to version 1.3.1

A fortify function method has been added to supplement the data fitted to a linear model with model fit statistics.
A describe_model function is added which can be used to get a short text summary of any DI model.
Meta-data about a DI model can be accessed via the attributes function.

Main changes in the package from version 1.2 to version 1.3

The DI and autoDI functions now have an additional parameter called ID which enables the user to group the species identity effects (see examples below).
The predict function now has flexibility to calculate confidence and prediction intervals for the predicted values.

Main changes in the package from version 1.1 to version 1.2

There are two new functions added to the package:
- predict: Make predictions from a fitted DI model without having to worry about theta, and the interaction terms in the data.
- contrasts_DI: Create contrasts for a DI model.

Main changes in the package from version 1.0 to version 1.1

DI_data_prepare is now superseded by DI_data (see examples below)

`DImodels` installation and load

The DImodels package is installed from CRAN and loaded in the typical way.

install.packages("DImodels")
library("DImodels")

Accessing an introduction to Diversity-Introductions models

It is recommended that users unfamiliar with Diversity-Interactions (DI) models read the introduction to DImodels, before using the package. Run the following code to access the documentation.

?DImodels

Datasets included in the DImodels package

There are seven example datasets included in the DImodels package: Bell, sim1, sim2, sim3, sim4, sim5, Switzerland. Details about each of these datasets is available in their associated help files, run this code, for example:

?sim3

In this vignette, we will describe the sim3 dataset and show a worked analysis of it.

The sim3 dataset

The sim3 dataset was simulated from a functional group (FG) Diversity-Interactions model. There were nine species in the pool, and it was assumed that species 1 to 5 come from functional group 1, species 6 and 7 from functional group 2 and species 8 and 9 from functional group 3, where species in the same functional group are assumed to have similar traits. The following equation was used to simulate the data.

$$ y = \sum_{i=1}^{9}\beta_ip_i + \omega_{11}\sum_{\substack{i,j = 1 \ i<j}}^5p_ip_j + \omega_{22}p_6p_7 + \omega_{33}p_8p_9 \ + \omega_{12}\sum_{\substack{i \in {1,2,3,4,5} \ j \in {6,7}}}p_ip_j + \omega_{13}\sum_{\substack{i \in {1,2,3,4,5} \ j \in {8,9}}}p_ip_j + \omega_{23}\sum_{\substack{i \in {6,7} \ j \in {8,9}}}p_ip_j + \gamma_k + \epsilon$$ Where $\gamma_k$ is a treatment effect with two levels (k = 1,2) and $\epsilon$ was assumed IID N(0, $\sigma^2$). The parameter values are in the following table.

Parameter	Value	Parameter	Value
$\beta_1$	10	$\omega_{11}$	2
$\beta_2$	9	$\omega_{22}$	3
$\beta_3$	8	$\omega_{33}$	1
$\beta_4$	7	$\omega_{12}$	4
$\beta_5$	11	$\omega_{13}$	9
$\beta_6$	6	$\omega_{23}$	3
$\beta_7$	5	$\gamma_1$	3
$\beta_8$	8	$\gamma_2$	0
$\beta_9$	9	$\sigma$	1.2

Here, the non-linear parameter $\theta$ that can be included as a power on each $p_ip_j$ component of each interaction variable (Connolly et al 2013) was set equal to one and thus does not appear in the equation above.

The 206 rows of proportions contained in the dataset design_a (supplied in the package) were used to simulate the sim3 dataset. Here is the first few rows from design_a:

community	richness	p7	p8	p9
1	1	0	0	1
1	1	0	0	1
2	1	0	1	0
2	1	0	1	0
3	1	1	0	0
3	1	1	0	0

Where community is an identifier for unique sets of proportions and richness is the number of species in the community.

The proportions in design_a were replicated over two treatment levels, giving a total of 412 rows in the simulated dataset. The sim3 data can be loaded and viewed in the usual way.

data("sim3")
knitr::kable(head(sim3, 10))

community	richness	treatment	p7	p8	p9	response
1	1	A	0	0	1	10.265
1	1	B	0	0	1	7.740
1	1	A	0	0	1	12.173
1	1	B	0	0	1	8.497
2	1	A	0	1	0	10.763
2	1	B	0	1	0	8.989
2	1	A	0	1	0	10.161
2	1	B	0	1	0	7.193
3	1	A	1	0	0	10.171
3	1	B	1	0	0	6.053

Exploring the data

There are several graphical displays that will help to explore the data and it may also be useful to generate summary statistics.

hist(sim3$response, xlab = "Response", main = "")

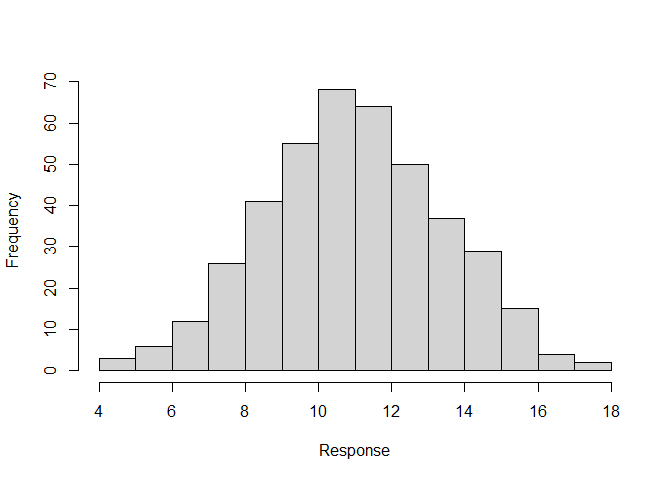
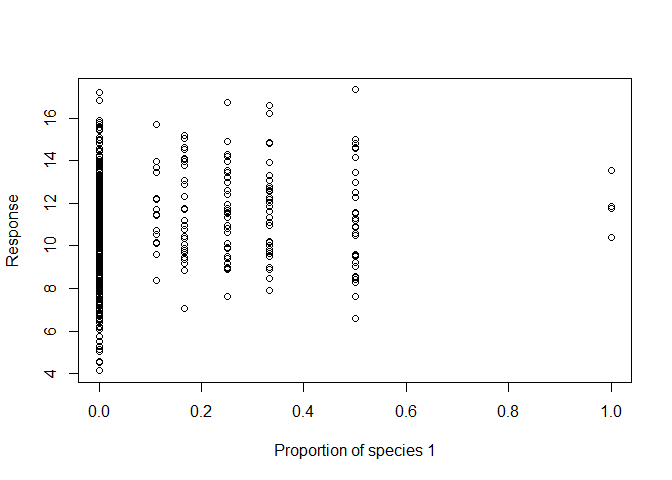
# Similar graphs can also be generated for the other species proportions.
plot(sim3$p1, sim3$response, xlab = "Proportion of species 1", ylab = "Response")

summary(sim3$response)
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   4.134   9.327  10.961  10.994  12.604  17.323

Implementing an automated DI model fitting process using `autoDI`

The function autoDI in DImodels provides a way to do an automated exploratory analysis to compare a range of DI models. It works through a set of automated steps (Steps 1 to 4) and will select the ‘best’ model from the range of models that have been explored and test for lack of fit in that model. The selection process is not exhaustive, but provides a useful starting point in analysis using DI models.

auto1 <- autoDI(y = "response", prop = 4:12, treat = "treatment", 
                FG = c("FG1","FG1","FG1","FG1","FG1","FG2","FG2","FG3","FG3"), data = sim3, 
                selection = "Ftest")
#> 
#> --------------------------------------------------------------------------------
#> Step 1: Investigating whether theta is equal to 1 or not for the AV model, including all available structures
#> 
#> Theta estimate: 0.9714
#> Selection using F tests
#>            Description                                                       
#> DI Model 1 Average interactions 'AV' DImodel with treatment                  
#> DI Model 2 Average interactions 'AV' DImodel with treatment, estimating theta
#> 
#>            DI_model       treat estimate_theta Resid. Df Resid. SSq Resid. MSq
#> DI Model 1       AV 'treatment'          FALSE       401   694.3095     1.7314
#> DI Model 2       AV 'treatment'           TRUE       400   693.7321     1.7343
#>            Df    SSq     F Pr(>F)
#> DI Model 1                       
#> DI Model 2  1 0.5775 0.333 0.5642
#> 
#> The test concludes that theta is not significantly different from 1.
#> 
#> --------------------------------------------------------------------------------
#> Step 2: Investigating the interactions
#> Since 'Ftest' was specified as selection criterion and functional groups were specified, dropping the ADD model as it is not nested within the FG model.
#> Selection using F tests
#>            Description                                                 
#> DI Model 1 Structural 'STR' DImodel with treatment                     
#> DI Model 2 Species identity 'ID' DImodel with treatment                
#> DI Model 3 Average interactions 'AV' DImodel with treatment            
#> DI Model 4 Functional group effects 'FG' DImodel with treatment        
#> DI Model 5 Separate pairwise interactions 'FULL' DImodel with treatment
#> 
#>            DI_model       treat estimate_theta Resid. Df Resid. SSq Resid. MSq
#> DI Model 1      STR 'treatment'          FALSE       410  1496.1645     3.6492
#> DI Model 2       ID 'treatment'          FALSE       402   841.2740     2.0927
#> DI Model 3       AV 'treatment'          FALSE       401   694.3095     1.7314
#> DI Model 4       FG 'treatment'          FALSE       396   559.7110     1.4134
#> DI Model 5     FULL 'treatment'          FALSE       366   522.9727     1.4289
#>            Df      SSq        F  Pr(>F)
#> DI Model 1                             
#> DI Model 2  8 654.8905  57.2903 <0.0001
#> DI Model 3  1 146.9645 102.8524 <0.0001
#> DI Model 4  5 134.5985  18.8396 <0.0001
#> DI Model 5 30  36.7383    0.857   0.686
#> 
#> Selected model: Functional group effects 'FG' DImodel with treatment
#> 
#> --------------------------------------------------------------------------------
#> Step 3: Investigating the treatment effect
#> Selection using F tests
#>            Description                                         
#> DI Model 1 Functional group effects 'FG' DImodel               
#> DI Model 2 Functional group effects 'FG' DImodel with treatment
#> 
#>            DI_model       treat estimate_theta Resid. Df Resid. SSq Resid. MSq
#> DI Model 1       FG        none          FALSE       397   1550.682     3.9060
#> DI Model 2       FG 'treatment'          FALSE       396    559.711     1.4134
#>            Df      SSq      F  Pr(>F)
#> DI Model 1                           
#> DI Model 2  1 990.9711 701.12 <0.0001
#> 
#> Selected model: Functional group effects 'FG' DImodel with treatment
#> 
#> --------------------------------------------------------------------------------
#> Step 4: Comparing the final selected model with the reference (community) model
#> 'community' is a factor with 100 levels, one for each unique set of proportions.
#> 
#>                model Resid. Df Resid. SSq Resid. MSq Df      SSq     F Pr(>F)
#> DI Model 1  Selected       396   559.7110     1.4134                         
#> DI Model 2 Reference       311   445.9889     1.4340 85 113.7222 0.933 0.6423
#> 
#> --------------------------------------------------------------------------------
#> autoDI is limited in terms of model selection. Exercise caution when choosing your final model.
#> --------------------------------------------------------------------------------

The output of autoDI, works through the following process:

Step 1 fitted the average interactions (AV) model and uses profile likelihood to estimate the non-linear parameter $\theta$ and tests whether or not it differs from one. $\theta$ was estimated to be 0.96814 and was not significantly different from one ($p = 0.4572$). Therefore, subsequent steps assumed $\theta=1$ when fitting the DI models.
Step 2 fitted five different DI models, each with a different form of species interactions and treatment was always included. The functional group model (FG) was the selected model. This assumes that pairs of species interact according to functional group membership.
Step 3 provided a test for the treatment and indicated that the treatment, included as an additive factor, was significant and needed in the model ($p < 0.0001$).
Step 4 provides a lack of fit test, here there was no indication of lack of fit in the model selected in Step 3 ($p = 0.6423$).

Further details on each of these steps are available in the autoDI help file. Run the following code to access the documentation.

?autoDI

All parameter estimates from the selected model can be viewed using summary.

summary(auto1)
#> 
#> Call:
#> glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Coefficients:
#>                Estimate Std. Error t value Pr(>|t|)    
#> p1_ID            9.7497     0.3666  26.595  < 2e-16 ***
#> p2_ID            8.5380     0.3672  23.253  < 2e-16 ***
#> p3_ID            8.2329     0.3666  22.459  < 2e-16 ***
#> p4_ID            6.3644     0.3665  17.368  < 2e-16 ***
#> p5_ID           10.8468     0.3669  29.561  < 2e-16 ***
#> p6_ID            5.9621     0.4515  13.205  < 2e-16 ***
#> p7_ID            5.4252     0.4516  12.015  < 2e-16 ***
#> p8_ID            7.3204     0.4515  16.213  < 2e-16 ***
#> p9_ID            8.2154     0.4515  18.196  < 2e-16 ***
#> FG_bfg_FG1_FG2   3.4395     0.8635   3.983 8.09e-05 ***
#> FG_bfg_FG1_FG3  11.5915     0.8654  13.395  < 2e-16 ***
#> FG_bfg_FG2_FG3   2.8711     1.2627   2.274  0.02351 *  
#> FG_wfg_FG1       2.8486     0.9131   3.120  0.00194 ** 
#> FG_wfg_FG2       0.6793     2.3553   0.288  0.77319    
#> FG_wfg_FG3       2.4168     2.3286   1.038  0.29997    
#> treatmentA       3.1018     0.1171  26.479  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.413412)
#> 
#>     Null deviance: 52280.33  on 412  degrees of freedom
#> Residual deviance:   559.71  on 396  degrees of freedom
#> AIC: 1329.4
#> 
#> Number of Fisher Scoring iterations: 2

If the final model selected by autoDI includes a value of theta other than 1, then a 95% confidence interval for $\theta$ can be generated using the theta_CI function:

theta_CI(auto1, conf = .95)

Here, this code would not run, since the final model selected by autoDI does not include theta estimated.

Fitting individual models using the `DI` function

For some users, the selection process in autoDI will be sufficient, however, most users will fit additional models using DI. For example, while the treatment is included in autoDI as an additive factor, interactions between treatment and other model terms are not considered. Here, we will first fit the model selected by autoDI using DI and then illustrate the capabilities of DI to fit specialised models.

Fitting the final model selected by `autoDI` using `DI`

m1 <- DI(y = "response", prop = 4:12, 
         FG = c("FG1","FG1","FG1","FG1","FG1","FG2","FG2","FG3","FG3"), treat = "treatment", 
         DImodel = "FG", data = sim3)
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
summary(m1)
#> 
#> Call:
#> glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Coefficients:
#>                Estimate Std. Error t value Pr(>|t|)    
#> p1_ID            9.7497     0.3666  26.595  < 2e-16 ***
#> p2_ID            8.5380     0.3672  23.253  < 2e-16 ***
#> p3_ID            8.2329     0.3666  22.459  < 2e-16 ***
#> p4_ID            6.3644     0.3665  17.368  < 2e-16 ***
#> p5_ID           10.8468     0.3669  29.561  < 2e-16 ***
#> p6_ID            5.9621     0.4515  13.205  < 2e-16 ***
#> p7_ID            5.4252     0.4516  12.015  < 2e-16 ***
#> p8_ID            7.3204     0.4515  16.213  < 2e-16 ***
#> p9_ID            8.2154     0.4515  18.196  < 2e-16 ***
#> FG_bfg_FG1_FG2   3.4395     0.8635   3.983 8.09e-05 ***
#> FG_bfg_FG1_FG3  11.5915     0.8654  13.395  < 2e-16 ***
#> FG_bfg_FG2_FG3   2.8711     1.2627   2.274  0.02351 *  
#> FG_wfg_FG1       2.8486     0.9131   3.120  0.00194 ** 
#> FG_wfg_FG2       0.6793     2.3553   0.288  0.77319    
#> FG_wfg_FG3       2.4168     2.3286   1.038  0.29997    
#> treatmentA       3.1018     0.1171  26.479  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.413412)
#> 
#>     Null deviance: 52280.33  on 412  degrees of freedom
#> Residual deviance:   559.71  on 396  degrees of freedom
#> AIC: 1329.4
#> 
#> Number of Fisher Scoring iterations: 2

Re-fitting the final model selected by `autoDI` estimating theta using `update_DI`

m1_theta <- update_DI(object = m1, estimate_theta = TRUE)
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
#> Theta estimate: 0.9681
coef(m1_theta)
#>          p1_ID          p2_ID          p3_ID          p4_ID          p5_ID 
#>      9.8128865      8.6069092      8.2968619      6.4287580     10.9110563 
#>          p6_ID          p7_ID          p8_ID          p9_ID FG_bfg_FG1_FG2 
#>      6.0189395      5.4846833      7.4038925      8.2992262      2.9840924 
#> FG_bfg_FG1_FG3 FG_bfg_FG2_FG3     FG_wfg_FG1     FG_wfg_FG2     FG_wfg_FG3 
#>     10.6019235      2.3514998      2.3737831      0.3789464      1.8470612 
#>     treatmentA          theta 
#>      3.1017864      0.9681005

Grouping the species identity effects in the model

The species identity effects in a DI model can be grouped by specifying groups for each species using the ID argument. The ID argument functions similar to the FG argument and accepts a character list of same length as number of species in the model. The identity effects of species belonging in the same group will be grouped together.

Grouping all identity effects into a single term

m1_group <- update_DI(object = m1_theta, 
                      ID = c("ID1", "ID1", "ID1", "ID1", "ID1",
                             "ID1", "ID1", "ID1", "ID1"))
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
#> Theta estimate: 0.9919
coef(m1_group)
#>            ID1 FG_bfg_FG1_FG2 FG_bfg_FG1_FG3 FG_bfg_FG2_FG3     FG_wfg_FG1 
#>      7.8667702      1.1475018     12.9438529     -1.2235215      5.6141823 
#>     FG_wfg_FG2     FG_wfg_FG3     treatmentA          theta 
#>     -5.5214662      1.0205019      3.1017864      0.9919097

Grouping identity effects of specific species

m1_group2 <- update_DI(object = m1_theta, 
                       ID = c("ID1", "ID1", "ID1", 
                              "ID2", "ID2", "ID2", 
                              "ID3", "ID3", "ID3"))
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
#> Theta estimate: 0.989
coef(m1_group2)
#>            ID1            ID2            ID3 FG_bfg_FG1_FG2 FG_bfg_FG1_FG3 
#>      8.5288216      7.9537767      7.1357104      0.9665077     13.3434768 
#> FG_bfg_FG2_FG3     FG_wfg_FG1     FG_wfg_FG2     FG_wfg_FG3     treatmentA 
#>      0.4940952      4.1543637     -4.4683501      3.4674196      3.1017864 
#>          theta 
#>      0.9889999

Note: Grouping ID effects will not have an effect on the calculation of the interaction effects, they would still be calculated by using all species.

Read the documentation of DI and autoDI for more information and examples using the ID parameter.

?DI
?autoDI

Fitting customised models using the `DI` function

There are two ways to fit customised models using DI; the first is by using the option DImodel = in the DI function and adding the argument extra_formula = to it, and the second is to use the custom_formula argument in the DI function. If species interaction variables (e.g., the FG interactions or the average pairwise interaction) are included in either extra_formula or custom_formula, they must first be created and included in the dataset. The function DI_data can be used to compute several types of species interaction variables.

Including treatment by species identity term interactions using `extra_formula`

m2 <- DI(y = "response", prop = 4:12, 
         FG = c("FG1","FG1","FG1","FG1","FG1","FG2","FG2","FG3","FG3"), treat = "treatment", 
         DImodel = "FG", extra_formula = ~ (p1 + p2 + p3 + p4):treatment,
         data = sim3)
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
summary(m2)
#> 
#> Call:
#> glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> p1_ID           10.018491   0.466552  21.473  < 2e-16 ***
#> p2_ID            8.494038   0.467009  18.188  < 2e-16 ***
#> p3_ID            7.970716   0.466536  17.085  < 2e-16 ***
#> p4_ID            6.624476   0.466443  14.202  < 2e-16 ***
#> p5_ID           10.802270   0.378776  28.519  < 2e-16 ***
#> p6_ID            5.917565   0.461482  12.823  < 2e-16 ***
#> p7_ID            5.380703   0.461535  11.658  < 2e-16 ***
#> p8_ID            7.275881   0.461506  15.766  < 2e-16 ***
#> p9_ID            8.170907   0.461471  17.706  < 2e-16 ***
#> FG_bfg_FG1_FG2   3.439508   0.865279   3.975 8.38e-05 ***
#> FG_bfg_FG1_FG3  11.591458   0.867140  13.367  < 2e-16 ***
#> FG_bfg_FG2_FG3   2.871063   1.265295   2.269  0.02381 *  
#> FG_wfg_FG1       2.848612   0.915008   3.113  0.00199 ** 
#> FG_wfg_FG2       0.679285   2.360195   0.288  0.77365    
#> FG_wfg_FG3       2.416774   2.333420   1.036  0.30097    
#> treatmentA       3.190868   0.216493  14.739  < 2e-16 ***
#> `treatmentA:p1` -0.626667   0.668369  -0.938  0.34902    
#> `treatmentA:p2` -0.001213   0.668369  -0.002  0.99855    
#> `treatmentA:p3`  0.435322   0.668369   0.651  0.51522    
#> `treatmentA:p4` -0.609180   0.668369  -0.911  0.36262    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.419257)
#> 
#>     Null deviance: 52280.33  on 412  degrees of freedom
#> Residual deviance:   556.35  on 392  degrees of freedom
#> AIC: 1335
#> 
#> Number of Fisher Scoring iterations: 2

Including treatment by species interaction terms using `extra_formula`

First, we create the FG pairwise interactions, using the DI_data function with the what argument set to "FG".

FG_matrix <- DI_data(prop = 4:12, FG = c("FG1","FG1","FG1","FG1","FG1","FG2","FG2","FG3","FG3"), 
                     data = sim3, what = "FG")
sim3a <- data.frame(sim3, FG_matrix)

Then we fit the model using extra_formula.

m3 <- DI(y = "response", prop = 4:12, 
         FG = c("FG1","FG1","FG1","FG1","FG1","FG2","FG2","FG3","FG3"),
         treat = "treatment", DImodel = "FG", 
         extra_formula = ~ (bfg_FG1_FG2 + bfg_FG1_FG3 + bfg_FG2_FG3 +
                              wfg_FG1 + wfg_FG2 + wfg_FG3) : treatment, data = sim3a)
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Functional group effects 'FG' DImodel
summary(m3)
#> 
#> Call:
#> glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Coefficients:
#>                          Estimate Std. Error t value Pr(>|t|)    
#> p1_ID                     9.68668    0.40000  24.217  < 2e-16 ***
#> p2_ID                     8.47495    0.40053  21.159  < 2e-16 ***
#> p3_ID                     8.16990    0.39998  20.426  < 2e-16 ***
#> p4_ID                     6.30140    0.39987  15.759  < 2e-16 ***
#> p5_ID                    10.78379    0.40031  26.938  < 2e-16 ***
#> p6_ID                     5.89908    0.47958  12.301  < 2e-16 ***
#> p7_ID                     5.36222    0.47963  11.180  < 2e-16 ***
#> p8_ID                     7.25740    0.47960  15.132  < 2e-16 ***
#> p9_ID                     8.15243    0.47957  17.000  < 2e-16 ***
#> FG_bfg_FG1_FG2            4.00191    1.12383   3.561 0.000415 ***
#> FG_bfg_FG1_FG3           11.77389    1.12973  10.422  < 2e-16 ***
#> FG_bfg_FG2_FG3            3.83681    1.64287   2.335 0.020027 *  
#> FG_wfg_FG1                2.81860    1.16226   2.425 0.015757 *  
#> FG_wfg_FG2               -1.58378    3.11717  -0.508 0.611682    
#> FG_wfg_FG3                1.32358    3.07561   0.430 0.667181    
#> treatmentA                3.22783    0.33480   9.641  < 2e-16 ***
#> `treatmentA:bfg_FG1_FG2` -1.12480    1.43053  -0.786 0.432178    
#> `treatmentA:bfg_FG1_FG3` -0.36487    1.44450  -0.253 0.800717    
#> `treatmentA:bfg_FG2_FG3` -1.93150    2.09024  -0.924 0.356029    
#> `treatmentA:wfg_FG1`      0.06003    1.42911   0.042 0.966517    
#> `treatmentA:wfg_FG2`      4.52613    4.06260   1.114 0.265924    
#> `treatmentA:wfg_FG3`      2.18638    3.99748   0.547 0.584733    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.42436)
#> 
#>     Null deviance: 52280.3  on 412  degrees of freedom
#> Residual deviance:   555.5  on 390  degrees of freedom
#> AIC: 1338.3
#> 
#> Number of Fisher Scoring iterations: 2

Fitting only a subset of the FG interaction terms using `custom_formula`

First, we create a dummy variable for level A of the treatment (this is required for the glm engine that is used within DI and because there is no intercept in the model).

sim3a$treatmentA <- as.numeric(sim3a$treatment == "A")

Then we fit the model using custom_formula.

m3 <- DI(y = "response",
         custom_formula = response ~ 0 + p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9 +
           treatmentA + bfg_FG1_FG2 + bfg_FG1_FG3 + bfg_FG2_FG3, data = sim3a)
#> Fitted model: Custom DI model
summary(m3)
#> 
#> Call:
#> glm(formula = custom_formula, family = family, data = data)
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> p1           10.3417     0.3138  32.957  < 2e-16 ***
#> p2            9.1766     0.3103  29.573  < 2e-16 ***
#> p3            8.8268     0.3134  28.164  < 2e-16 ***
#> p4            6.9742     0.3122  22.341  < 2e-16 ***
#> p5           11.4422     0.3141  36.426  < 2e-16 ***
#> p6            5.9177     0.3994  14.815  < 2e-16 ***
#> p7            5.3967     0.3999  13.496  < 2e-16 ***
#> p8            7.4468     0.3983  18.695  < 2e-16 ***
#> p9            8.3449     0.3984  20.945  < 2e-16 ***
#> treatmentA    3.1018     0.1184  26.198  < 2e-16 ***
#> bfg_FG1_FG2   2.9359     0.8042   3.651 0.000296 ***
#> bfg_FG1_FG3  10.8896     0.8343  13.053  < 2e-16 ***
#> bfg_FG2_FG3   2.9410     1.2233   2.404 0.016667 *  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for gaussian family taken to be 1.443887)
#> 
#>     Null deviance: 52280.33  on 412  degrees of freedom
#> Residual deviance:   576.11  on 399  degrees of freedom
#> AIC: 1335.3
#> 
#> Number of Fisher Scoring iterations: 2

Making predictions and testing contrasts for DI models

Predictions using a DI model

We can make predictions from a DI model just like any other regression model using the predict function. The user does not need to worry about adding any interaction terms or adjusting any columns if theta is not equal to 1. Only the species proportions along with any additional experimental structures is needed and all other terms in the model will be calculated for the user.

# Fit model
m3 <- DI(y = "response", prop = 4:12, 
         treat = "treatment", DImodel = "AV", 
         extra_formula = ~ (AV) : treatment, data = sim3a)
#> Warning in DI_data_prepare(y = y, block = block, density = density, prop = prop, : One or more rows have species proportions that sum to approximately 1, but not exactly 1. This is typically a rounding issue, and has been corrected internally prior to analysis.
#> Fitted model: Average interactions 'AV' DImodel

predict_data <- sim3[c(1, 79, 352), 3:12]
# Only species proportions and treatment is needed
print(predict_data)
#>     treatment p1 p2        p3 p4        p5        p6        p7        p8
#> 1           A  0  0 0.0000000  0 0.0000000 0.0000000 0.0000000 0.0000000
#> 79          A  0  0 0.0000000  0 0.5000000 0.0000000 0.0000000 0.5000000
#> 352         B  0  0 0.1666667  0 0.1666667 0.1666667 0.1666667 0.1666667
#>            p9
#> 1   1.0000000
#> 79  0.0000000
#> 352 0.1666667
# Make prediction
predict(m3, newdata = predict_data)
#>        1       79      352 
#> 12.83789 14.27503 10.00291

Uncertainity around predictions

# The interval and level parameters can be used to calculate the 
# uncertainty around the predictions

# Get confidence interval around prediction
predict(m3, newdata = predict_data, interval = "confidence")
#>          fit       lwr      upr
#> 1   12.83789 12.028716 13.64707
#> 79  14.27503 13.817612 14.73246
#> 352 10.00291  9.694552 10.31126

# Get prediction interval around prediction
predict(m3, newdata = predict_data, interval = "prediction")
#>          fit       lwr      upr
#> 1   12.83789 10.124779 15.55100
#> 79  14.27503 11.645310 16.90476
#> 352 10.00291  7.394976 12.61083

# The function returns a 95% interval by default, 
# this can be changed using the level argument
predict(m3, newdata = predict_data, 
        interval = "prediction", level = 0.9)
#>          fit       lwr      upr
#> 1   12.83789 10.562595 15.11319
#> 79  14.27503 12.069670 16.48040
#> 352 10.00291  7.815819 12.18999

Contrasts for DI models

The contrasts_DI function can be used to compare and formally test for a difference in performance of communities within the same as well as across different experimental structures

Comparing the performance of the monocultures of different species at treatment A

contr <- list("p1vsp2" = c(1, -1, 0, 0,  0,  0, 0, 0,  0, 0, 0, 0),
              "p3vsp5" = c(0,  0, 1, 0, -1,  0, 0, 0,  0, 0, 0, 0),
              "p4vsp6" = c(0,  0, 0, 1,  0, -1, 0, 0,  0, 0, 0, 0),
              "p7vsp9" = c(0,  0, 0, 0,  0,  0, 1, 0, -1, 0, 0, 0))
the_C <- contrasts_DI(m3, contrast = contr)
#> Generated contrast matrix:
#>        p1_ID p2_ID p3_ID p4_ID p5_ID p6_ID p7_ID p8_ID p9_ID AV treatmentA
#> p1vsp2     1    -1     0     0     0     0     0     0     0  0          0
#> p3vsp5     0     0     1     0    -1     0     0     0     0  0          0
#> p4vsp6     0     0     0     1     0    -1     0     0     0  0          0
#> p7vsp9     0     0     0     0     0     0     1     0    -1  0          0
#>        `AV:treatmentB`
#> p1vsp2               0
#> p3vsp5               0
#> p4vsp6               0
#> p7vsp9               0
summary(the_C)
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Fit: glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Linear Hypotheses:
#>             Estimate Std. Error z value Pr(>|z|)    
#> p1vsp2 == 0    1.473      0.477   3.088  0.00803 ** 
#> p3vsp5 == 0   -2.652      0.477  -5.560 1.08e-07 ***
#> p4vsp6 == 0    1.462      0.477   3.064  0.00870 ** 
#> p7vsp9 == 0   -5.521      0.477 -11.573  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

Comparing across the two treatment levels for monoculture of species 1

contr <- list("treatAvsB" = c(1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0))
the_C <- contrasts_DI(m3, contrast = contr)
#> Generated contrast matrix:
#>           p1_ID p2_ID p3_ID p4_ID p5_ID p6_ID p7_ID p8_ID p9_ID AV treatmentA
#> treatAvsB     1     0     0     0     0     0     0     0     0  0          1
#>           `AV:treatmentB`
#> treatAvsB               0
summary(the_C)
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Fit: glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Linear Hypotheses:
#>                Estimate Std. Error z value Pr(>|z|)    
#> treatAvsB == 0  12.8993     0.4116   31.34   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

Comparing between two species mixtures

mixA <- c(0.25, 0,      0.25, 0,      0.25, 0,      0.25, 0, 0, 0, 0, 0)
mixB <- c(0,    0.3333, 0,    0.3333, 0,    0.3333, 0,    0, 0, 0, 0, 0)

# We have the proportions of the individual species in the mixtures, however
# we still need to calculate the interaction effect for these communities
contr_data <- data.frame(rbind(mixA, mixB))
colnames(contr_data) <- names(coef(m3))

# Adding the interaction effect of the two mixtures
contr_data$AV <- DI_data_E_AV(prop = 1:9, data = contr_data)$AV
print(contr_data)
#>      p1_ID  p2_ID p3_ID  p4_ID p5_ID  p6_ID p7_ID p8_ID p9_ID        AV
#> mixA  0.25 0.0000  0.25 0.0000  0.25 0.0000  0.25     0     0 0.3750000
#> mixB  0.00 0.3333  0.00 0.3333  0.00 0.3333  0.00     0     0 0.3332667
#>      treatmentA `AV:treatmentB`
#> mixA          0               0
#> mixB          0               0

# We can now subtract the respective values in each column of the two 
# mixtures and get our contrast
my_contrast <- as.matrix(contr_data[1, ] - contr_data[2, ])
rownames(my_contrast) <- "mixAvsB"

the_C <- contrasts_DI(m3, contrast = my_contrast)
#> Generated contrast matrix:
#>         p1_ID   p2_ID p3_ID   p4_ID p5_ID   p6_ID p7_ID p8_ID p9_ID         AV
#> mixAvsB  0.25 -0.3333  0.25 -0.3333  0.25 -0.3333  0.25     0     0 0.04173333
#>         treatmentA `AV:treatmentB`
#> mixAvsB          0               0
summary(the_C)
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Fit: glm(formula = new_fmla, family = family, data = new_data)
#> 
#> Linear Hypotheses:
#>              Estimate Std. Error z value Pr(>|z|)    
#> mixAvsB == 0   2.0379     0.2599   7.841 4.44e-15 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

References

Connolly J, T Bell, T Bolger, C Brophy, T Carnus, JA Finn, L Kirwan, F Isbell, J Levine, A Lüscher, V Picasso, C Roscher, MT Sebastia, M Suter and A Weigelt (2013) An improved model to predict the effects of changing biodiversity levels on ecosystem function. Journal of Ecology, 101, 344-355.

Kirwan L, J Connolly, JA Finn, C Brophy, A Lüscher, D Nyfeler and MT Sebastia (2009) Diversity-interaction modelling - estimating contributions of species identities and interactions to ecosystem function. Ecology, 90, 2032-2038.

r-DImodels

DImodels

`DImodels` installation and load

Accessing an introduction to Diversity-Introductions models

Datasets included in the DImodels package

The sim3 dataset

Exploring the data

Implementing an automated DI model fitting process using `autoDI`

Fitting individual models using the `DI` function

Fitting the final model selected by `autoDI` using `DI`

Re-fitting the final model selected by `autoDI` estimating theta using `update_DI`

Grouping the species identity effects in the model

Fitting customised models using the `DI` function

Including treatment by species identity term interactions using `extra_formula`

Including treatment by species interaction terms using `extra_formula`

Fitting only a subset of the FG interaction terms using `custom_formula`

Making predictions and testing contrasts for DI models

Predictions using a DI model

Uncertainity around predictions

Contrasts for DI models

References

Version

License

Status

Source

Homepage

Platforms (75)

community	richness	p7	p8	p9
1	1	0	0	1
1	1	0	0	1
2	1	0	1	0
2	1	0	1	0
3	1	1	0	0
3	1	1	0	0

community	richness	p7	p8	p9
1	1	0	0	1
1	1	0	0	1
2	1	0	1	0
2	1	0	1	0
3	1	1	0	0
3	1	1	0	0

DImodels

DImodels installation and load

Accessing an introduction to Diversity-Introductions models

Datasets included in the DImodels package

The sim3 dataset

Exploring the data

Implementing an automated DI model fitting process using autoDI

Fitting individual models using the DI function

Fitting the final model selected by autoDI using DI

Re-fitting the final model selected by autoDI estimating theta using update_DI

Grouping the species identity effects in the model

Fitting customised models using the DI function

Including treatment by species identity term interactions using extra_formula

Including treatment by species interaction terms using extra_formula

Fitting only a subset of the FG interaction terms using custom_formula

Making predictions and testing contrasts for DI models

Predictions using a DI model

Uncertainity around predictions

Contrasts for DI models

References

Version

License

Status

Source

Homepage

Platforms75 (75)

`DImodels` installation and load

Implementing an automated DI model fitting process using `autoDI`

Fitting individual models using the `DI` function

Fitting the final model selected by `autoDI` using `DI`

Re-fitting the final model selected by `autoDI` estimating theta using `update_DI`

Fitting customised models using the `DI` function

Including treatment by species identity term interactions using `extra_formula`

Including treatment by species interaction terms using `extra_formula`

Fitting only a subset of the FG interaction terms using `custom_formula`

Platforms (75)

community	richness	p7	p8	p9
1	1	0	0	1
1	1	0	0	1
2	1	0	1	0
2	1	0	1	0
3	1	1	0	0
3	1	1	0	0