Description
IntraClass Effect Decomposition.
Description
Estimate test-retest reliability for complex sampling strategies and extract variances using IntraClass Effect Decomposition. Developed by Brandmaier et al. (2018) "Assessing reliability in neuroimaging research through intra-class effect decomposition (ICED)" <doi:10.7554/eLife.35718> Also includes functions to simulate data based on sampling strategy. Unofficial version release name: "Good work squirrels".
README.md
ICED
library("lavaan")
## This is lavaan 0.6-8
## lavaan is FREE software! Please report any bugs.
source("R/ICED_syntax.R")
source("R/ICED_run.R")
source("R/ICED_boot.R")
source("R/str2cov.R")
source("R/sim_ICED.R")
ICED: IntraClass Effect Decomposition
This script is intended to highlight progress and functionality with the ICED package
generate syntax
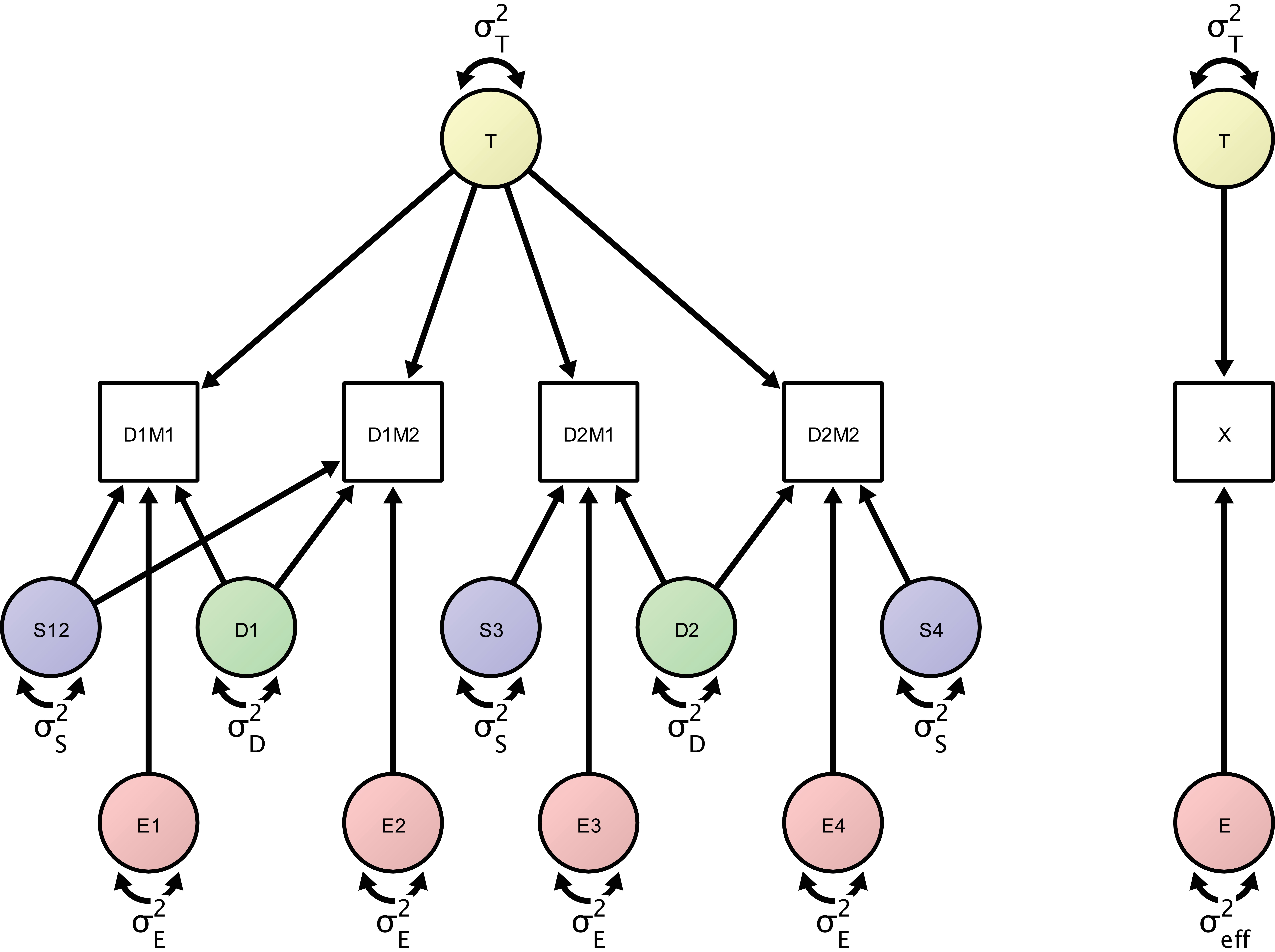
The ICED_syntax() function takes a dataframe and generates the lavaan syntax to run the model (the first variable must be time). Here we save it to the syn object. The model will also be printed to the console. We are aiming to recreate the model from Brandmaier et al. (2018), Figure 4
struc <- data.frame(time = c("T1", "T2", "T3", "T4"),
day = c("day1","day1","day2","day2"),
session = c("ses1", "ses1","ses2", "ses3"))
syn <- iced_syntax(struc)
## ! regressions
## T =~ 1*T1
## T =~ 1*T2
## T =~ 1*T3
## T =~ 1*T4
## day1 =~ 1*T1
## day1 =~ 1*T2
## day2 =~ 1*T3
## day2 =~ 1*T4
## ses1 =~ 1*T1
## ses1 =~ 1*T2
## ses2 =~ 1*T3
## ses3 =~ 1*T4
## E1 =~ 1*T1
## E2 =~ 1*T2
## E3 =~ 1*T3
## E4 =~ 1*T4
## ! residuals, variances and covariances
## T ~~ time*T
## day1 ~~ day*day1
## day2 ~~ day*day2
## ses1 ~~ session*ses1
## ses2 ~~ session*ses2
## ses3 ~~ session*ses3
## E1 ~~ e*E1
## E2 ~~ e*E2
## E3 ~~ e*E3
## E4 ~~ e*E4
## T ~~ 0*day1
## T ~~ 0*day2
## T ~~ 0*ses1
## T ~~ 0*ses2
## T ~~ 0*ses3
## T ~~ 0*E1
## T ~~ 0*E2
## T ~~ 0*E3
## T ~~ 0*E4
## day1 ~~ 0*day2
## day1 ~~ 0*ses1
## day1 ~~ 0*ses2
## day1 ~~ 0*ses3
## day1 ~~ 0*E1
## day1 ~~ 0*E2
## day1 ~~ 0*E3
## day1 ~~ 0*E4
## day2 ~~ 0*ses1
## day2 ~~ 0*ses2
## day2 ~~ 0*ses3
## day2 ~~ 0*E1
## day2 ~~ 0*E2
## day2 ~~ 0*E3
## day2 ~~ 0*E4
## ses1 ~~ 0*ses2
## ses1 ~~ 0*ses3
## ses1 ~~ 0*E1
## ses1 ~~ 0*E2
## ses1 ~~ 0*E3
## ses1 ~~ 0*E4
## ses2 ~~ 0*ses3
## ses2 ~~ 0*E1
## ses2 ~~ 0*E2
## ses2 ~~ 0*E3
## ses2 ~~ 0*E4
## ses3 ~~ 0*E1
## ses3 ~~ 0*E2
## ses3 ~~ 0*E3
## ses3 ~~ 0*E4
## E1 ~~ 0*E2
## E1 ~~ 0*E3
## E1 ~~ 0*E4
## E2 ~~ 0*E3
## E2 ~~ 0*E4
## E3 ~~ 0*E4
## ! observed means
## T1~1
## T2~1
## T3~1
## T4~1
## !set lower bounds of variances
## time > 0.0001
## day > 0.0001
## session > 0.0001
## e > 0.0001
simulate data
We’ll simulate data to run the ICED model on. The sim_ICED function takes the model structure dataframe we used earlier and a list of variances for each latent variable. The function returns several outputs, including the simulated data.
sim1 <- sim_ICED(struc,
variances = list(time = 10,
day = 2,
session = 1,
error = 3),
n = 2000)
head(sim1$data)
## T1 T2 T3 T4
## 1 -6.892969387 -6.5932264 -8.723213 -7.6298887
## 2 2.563843435 6.7974728 1.521446 3.0070102
## 3 3.750682653 2.0135844 1.898953 3.3198217
## 4 -0.008140112 0.8534418 -2.378560 -0.9479120
## 5 -2.319533037 -2.1481638 -3.104065 -0.6225882
## 6 3.568513686 0.6051093 1.038575 -3.9176493
we can also examine how well sim_ICED has recovered our variance parameters by setting check_recovery = TRUE. lets simulate two datasets, one large and another small.
sim2 <- sim_ICED(struc,
variances = list(time = 10,
day = 2,
session = 1,
error = 3),
n = 2000,
check_recovery = TRUE)
## [1] "n = 2000 data simulated"
## [1] "data simulated based on ICC1 = 0.625"
## time day session error
## 10 2 1 3
## [1] "model parameters recovered:"
## [1] "ICC1 = 0.644583202724004"
## timeest dayest sessionest eest
## 10.5419826 1.9993960 0.8164775 2.9968714
sim3 <- sim_ICED(struc,
variances = list(time = 10,
day = 2,
session = 1,
error = 3),
n = 20,
check_recovery = TRUE)
## [1] "n = 20 data simulated"
## [1] "data simulated based on ICC1 = 0.625"
## time day session error
## 10 2 1 3
## [1] "model parameters recovered:"
## [1] "ICC1 = 0.540163701082888"
## timeest dayest sessionest eest
## 6.4965675 0.5116045 2.2645328 2.7543297
str2cov
The sim_ICED function uses a helper function str2cov, which takes the same structure data.frame and the list of variances we specified earlier to generate the expected covariance of the model. This is then passed to mvrnorm to generate the data. e.g.
str2cov(struc,
list(time = 10,
day = 2,
session = 1,
error = 3),
e_label = "error")
## T1 T2 T3 T4
## T1 16 13 10 10
## T2 13 16 10 10
## T3 10 10 16 12
## T4 10 10 12 16
run_ICED
we can now run our model. The run_ICED function will print a bunch of relevant outputs. Note that the sim_ICED function returns a list of objects, so we need to specify the data part
res1 <- run_ICED(model = syn,
data = sim1$data)
## $ICC
## [1] 0.6315415
##
## $ICC2
## [1] 0.828968
##
## $timeest
## [1] 10.12744
##
## $dayest
## [1] 2.023995
##
## $sessionest
## [1] 0.8988333
##
## $eest
## [1] 2.985794
##
## $EffectiveError
## [1] 2.089485
##
## $AbsoluteError
## [1] 2.058057
##
## $phi_dependability
## [1] 0.831106
##
## $lavaan
## lavaan 0.6-8 ended normally after 209 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 14
## Number of inequality constraints 4
##
## Number of observations 2000
## Number of missing patterns 1
##
## Model Test User Model:
##
## Test statistic 3.685
## Degrees of freedom 6
## P-value (Chi-square) 0.719
##
## $est_cov
## T1 T2 T3 T4
## T1 16.036
## T2 13.050 16.036
## T3 10.127 10.127 16.036
## T4 10.127 10.127 12.151 16.036
we can also bootstrap our estimates. The output now includes 95% CIs on the ICC and ICC2. Best to use more than 10 boots, but set to 10 for speed here
run_ICED(model = syn,
data = sim1$data,
boot = 10)
## Warning in norm.inter(t, alpha): extreme order statistics used as endpoints
## Warning in norm.inter(t, alpha): extreme order statistics used as endpoints
## $ICC
## [1] 0.6315415
##
## $ICC_CIs
## [1] 0.6190221 0.6469655
##
## $ICC2
## [1] 0.828968
##
## $ICC2_CIs
## [1] 0.8237431 0.8462589
##
## $timeest
## [1] 10.12744
##
## $dayest
## [1] 2.023995
##
## $sessionest
## [1] 0.8988333
##
## $eest
## [1] 2.985794
##
## $EffectiveError
## [1] 2.089485
##
## $AbsoluteError
## [1] 2.058057
##
## $phi_dependability
## [1] 0.831106
##
## $lavaan
## lavaan 0.6-8 ended normally after 209 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 14
## Number of inequality constraints 4
##
## Number of observations 2000
## Number of missing patterns 1
##
## Model Test User Model:
##
## Test statistic 3.685
## Degrees of freedom 6
## P-value (Chi-square) 0.719
##
## $est_cov
## T1 T2 T3 T4
## T1 16.036
## T2 13.050 16.036
## T3 10.127 10.127 16.036
## T4 10.127 10.127 12.151 16.036
model comparison
we can compare alternative models, for example constraining the variance of one component to zero
syntax2 <- iced_syntax(struc,
set_variances = c(res1$timeest,
res1$dayest,
0,
res1$eest))
## Warning in iced_syntax(struc, set_variances = c(res1$timeest, res1$dayest, :
## set_variances must be list
## ! regressions
## T =~ 1*T1
## T =~ 1*T2
## T =~ 1*T3
## T =~ 1*T4
## day1 =~ 1*T1
## day1 =~ 1*T2
## day2 =~ 1*T3
## day2 =~ 1*T4
## ses1 =~ 1*T1
## ses1 =~ 1*T2
## ses2 =~ 1*T3
## ses3 =~ 1*T4
## E1 =~ 1*T1
## E2 =~ 1*T2
## E3 =~ 1*T3
## E4 =~ 1*T4
## ! residuals, variances and covariances
## T ~~ time*T
## day1 ~~ day*day1
## day2 ~~ day*day2
## ses1 ~~ session*ses1
## ses2 ~~ session*ses2
## ses3 ~~ session*ses3
## E1 ~~ e*E1
## E2 ~~ e*E2
## E3 ~~ e*E3
## E4 ~~ e*E4
## T ~~ 0*day1
## T ~~ 0*day2
## T ~~ 0*ses1
## T ~~ 0*ses2
## T ~~ 0*ses3
## T ~~ 0*E1
## T ~~ 0*E2
## T ~~ 0*E3
## T ~~ 0*E4
## day1 ~~ 0*day2
## day1 ~~ 0*ses1
## day1 ~~ 0*ses2
## day1 ~~ 0*ses3
## day1 ~~ 0*E1
## day1 ~~ 0*E2
## day1 ~~ 0*E3
## day1 ~~ 0*E4
## day2 ~~ 0*ses1
## day2 ~~ 0*ses2
## day2 ~~ 0*ses3
## day2 ~~ 0*E1
## day2 ~~ 0*E2
## day2 ~~ 0*E3
## day2 ~~ 0*E4
## ses1 ~~ 0*ses2
## ses1 ~~ 0*ses3
## ses1 ~~ 0*E1
## ses1 ~~ 0*E2
## ses1 ~~ 0*E3
## ses1 ~~ 0*E4
## ses2 ~~ 0*ses3
## ses2 ~~ 0*E1
## ses2 ~~ 0*E2
## ses2 ~~ 0*E3
## ses2 ~~ 0*E4
## ses3 ~~ 0*E1
## ses3 ~~ 0*E2
## ses3 ~~ 0*E3
## ses3 ~~ 0*E4
## E1 ~~ 0*E2
## E1 ~~ 0*E3
## E1 ~~ 0*E4
## E2 ~~ 0*E3
## E2 ~~ 0*E4
## E3 ~~ 0*E4
## ! observed means
## T1~1
## T2~1
## T3~1
## T4~1
## !set variances
##
## time == 10.1274398251025
## day == 2.02399517103763
## session == 0
## e == 2.98579433458071
res2 <- run_ICED(syntax2,
sim1$data)
## $ICC
## [1] 0.6690418
##
## $ICC2
## [1] 0.8520559
##
## $timeest
## [1] 10.12744
##
## $dayest
## [1] 2.023995
##
## $sessionest
## [1] 0
##
## $eest
## [1] 2.985794
##
## $EffectiveError
## [1] 1.758446
##
## $AbsoluteError
## [1] 1.758446
##
## $phi_dependability
## [1] 0.8520559
##
## $lavaan
## lavaan 0.6-8 ended normally after 1 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 14
## Number of equality constraints 10
##
## Number of observations 2000
## Number of missing patterns 1
##
## Model Test User Model:
##
## Test statistic 113.780
## Degrees of freedom 10
## P-value (Chi-square) 0.000
##
## $est_cov
## T1 T2 T3 T4
## T1 15.137
## T2 12.151 15.137
## T3 10.127 10.127 15.137
## T4 10.127 10.127 12.151 15.137
anova(res1$lavaan,
res2$lavaan)
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## res1$lavaan 6 39651 39696 3.6852
## res2$lavaan 10 39753 39776 113.7797 110.09 4 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
group comparisons
we can use iced_syntax to generate the syntax for multiple groups. The user can specify a number of groups or a vector of strings. Here we’ll also highlight that we can set the variances to be greater than zero also.
group_syntax <- iced_syntax(struc,
groups = 2,
fix_lower_bounds = TRUE)
## ! regressions
## T =~ 1*T1
## T =~ 1*T2
## T =~ 1*T3
## T =~ 1*T4
## day1 =~ 1*T1
## day1 =~ 1*T2
## day2 =~ 1*T3
## day2 =~ 1*T4
## ses1 =~ 1*T1
## ses1 =~ 1*T2
## ses2 =~ 1*T3
## ses3 =~ 1*T4
## E1 =~ 1*T1
## E2 =~ 1*T2
## E3 =~ 1*T3
## E4 =~ 1*T4
## ! residuals, variances and covariances
## T ~~ c(lattime1,lattime2)*T
## day1 ~~ c(latday1,latday2)*day1
## day2 ~~ c(latday1,latday2)*day2
## ses1 ~~ c(latsession1,latsession2)*ses1
## ses2 ~~ c(latsession1,latsession2)*ses2
## ses3 ~~ c(latsession1,latsession2)*ses3
## E1 ~~ c(late1,late2)*E1
## E2 ~~ c(late1,late2)*E2
## E3 ~~ c(late1,late2)*E3
## E4 ~~ c(late1,late2)*E4
## T ~~ 0*day1
## T ~~ 0*day2
## T ~~ 0*ses1
## T ~~ 0*ses2
## T ~~ 0*ses3
## T ~~ 0*E1
## T ~~ 0*E2
## T ~~ 0*E3
## T ~~ 0*E4
## day1 ~~ 0*day2
## day1 ~~ 0*ses1
## day1 ~~ 0*ses2
## day1 ~~ 0*ses3
## day1 ~~ 0*E1
## day1 ~~ 0*E2
## day1 ~~ 0*E3
## day1 ~~ 0*E4
## day2 ~~ 0*ses1
## day2 ~~ 0*ses2
## day2 ~~ 0*ses3
## day2 ~~ 0*E1
## day2 ~~ 0*E2
## day2 ~~ 0*E3
## day2 ~~ 0*E4
## ses1 ~~ 0*ses2
## ses1 ~~ 0*ses3
## ses1 ~~ 0*E1
## ses1 ~~ 0*E2
## ses1 ~~ 0*E3
## ses1 ~~ 0*E4
## ses2 ~~ 0*ses3
## ses2 ~~ 0*E1
## ses2 ~~ 0*E2
## ses2 ~~ 0*E3
## ses2 ~~ 0*E4
## ses3 ~~ 0*E1
## ses3 ~~ 0*E2
## ses3 ~~ 0*E3
## ses3 ~~ 0*E4
## E1 ~~ 0*E2
## E1 ~~ 0*E3
## E1 ~~ 0*E4
## E2 ~~ 0*E3
## E2 ~~ 0*E4
## E3 ~~ 0*E4
## ! observed means
## T1~1
## T2~1
## T3~1
## T4~1
## !set lower bounds of variances
## lattime1 > 0.0001
## lattime2 > 0.0001
## latday1 > 0.0001
## latday2 > 0.0001
## latsession1 > 0.0001
## latsession2 > 0.0001
## late1 > 0.0001
## late2 > 0.0001
group_syntax <- iced_syntax(struc,
groups = c("group1", "group2"),
fix_lower_bounds = TRUE)
## ! regressions
## T =~ 1*T1
## T =~ 1*T2
## T =~ 1*T3
## T =~ 1*T4
## day1 =~ 1*T1
## day1 =~ 1*T2
## day2 =~ 1*T3
## day2 =~ 1*T4
## ses1 =~ 1*T1
## ses1 =~ 1*T2
## ses2 =~ 1*T3
## ses3 =~ 1*T4
## E1 =~ 1*T1
## E2 =~ 1*T2
## E3 =~ 1*T3
## E4 =~ 1*T4
## ! residuals, variances and covariances
## T ~~ c(lattimegroup1,lattimegroup2)*T
## day1 ~~ c(latdaygroup1,latdaygroup2)*day1
## day2 ~~ c(latdaygroup1,latdaygroup2)*day2
## ses1 ~~ c(latsessiongroup1,latsessiongroup2)*ses1
## ses2 ~~ c(latsessiongroup1,latsessiongroup2)*ses2
## ses3 ~~ c(latsessiongroup1,latsessiongroup2)*ses3
## E1 ~~ c(lategroup1,lategroup2)*E1
## E2 ~~ c(lategroup1,lategroup2)*E2
## E3 ~~ c(lategroup1,lategroup2)*E3
## E4 ~~ c(lategroup1,lategroup2)*E4
## T ~~ 0*day1
## T ~~ 0*day2
## T ~~ 0*ses1
## T ~~ 0*ses2
## T ~~ 0*ses3
## T ~~ 0*E1
## T ~~ 0*E2
## T ~~ 0*E3
## T ~~ 0*E4
## day1 ~~ 0*day2
## day1 ~~ 0*ses1
## day1 ~~ 0*ses2
## day1 ~~ 0*ses3
## day1 ~~ 0*E1
## day1 ~~ 0*E2
## day1 ~~ 0*E3
## day1 ~~ 0*E4
## day2 ~~ 0*ses1
## day2 ~~ 0*ses2
## day2 ~~ 0*ses3
## day2 ~~ 0*E1
## day2 ~~ 0*E2
## day2 ~~ 0*E3
## day2 ~~ 0*E4
## ses1 ~~ 0*ses2
## ses1 ~~ 0*ses3
## ses1 ~~ 0*E1
## ses1 ~~ 0*E2
## ses1 ~~ 0*E3
## ses1 ~~ 0*E4
## ses2 ~~ 0*ses3
## ses2 ~~ 0*E1
## ses2 ~~ 0*E2
## ses2 ~~ 0*E3
## ses2 ~~ 0*E4
## ses3 ~~ 0*E1
## ses3 ~~ 0*E2
## ses3 ~~ 0*E3
## ses3 ~~ 0*E4
## E1 ~~ 0*E2
## E1 ~~ 0*E3
## E1 ~~ 0*E4
## E2 ~~ 0*E3
## E2 ~~ 0*E4
## E3 ~~ 0*E4
## ! observed means
## T1~1
## T2~1
## T3~1
## T4~1
## !set lower bounds of variances
## lattimegroup1 > 0.0001
## lattimegroup2 > 0.0001
## latdaygroup1 > 0.0001
## latdaygroup2 > 0.0001
## latsessiongroup1 > 0.0001
## latsessiongroup2 > 0.0001
## lategroup1 > 0.0001
## lategroup2 > 0.0001
generating multiple group data takes a few more lines of code currently - but I plan to adapt this to take vectors within the lists.
variances_hi <- list(time = 8,
day = .25,
session = .2,
error = .25)
variances_lo <- list(time = 2,
day = .25,
session = .2,
error = .25)
sim_hi <- sim_ICED(structure = struc,
variances = variances_hi,
n = 100)$data
sim_lo <- sim_ICED(structure = struc,
variances = variances_lo,
n = 100)$data
sim_hi$group <- "high"
sim_lo$group <- "low"
sim_all <- rbind(sim_hi, sim_lo)
we can check the ICC reliability we have specified fairly easily, e.g. for the high group variances_hi$time / (sum(unlist(variances_hi))). For the high group ICC = 0.9195402, and the low group ICC = 0.7407407.
Then we can compare the groups (not currenly within run_ICED). Here, m0 is our base model constraining variances across groups, and m1 using the model we just generated to allow them to vary across groups.
m1 <- lavaan::lavaan(model = group_syntax,
data = sim_all,
group = "group")
m0 <- lavaan::lavaan(model = syn,
data = sim_all,
group = "group")
## Warning in lavaanify(model = FLAT, constraints = constraints, varTable = lavdata@ov, : lavaan WARNING: using a single label per parameter in a multiple group
## setting implies imposing equality constraints across all the groups;
## If this is not intended, either remove the label(s), or use a vector
## of labels (one for each group);
## See the Multiple groups section in the man page of model.syntax.
summary(m1)
## lavaan 0.6-8 ended normally after 376 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 28
## Number of inequality constraints 8
##
## Number of observations per group:
## high 100
## low 100
##
## Model Test User Model:
##
## Test statistic 15.425
## Degrees of freedom 12
## P-value (Chi-square) 0.219
## Test statistic for each group:
## high 7.306
## low 8.119
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
##
## Group 1 [high]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## T =~
## T1 1.000
## T2 1.000
## T3 1.000
## T4 1.000
## day1 =~
## T1 1.000
## T2 1.000
## day2 =~
## T3 1.000
## T4 1.000
## ses1 =~
## T1 1.000
## T2 1.000
## ses2 =~
## T3 1.000
## ses3 =~
## T4 1.000
## E1 =~
## T1 1.000
## E2 =~
## T2 1.000
## E3 =~
## T3 1.000
## E4 =~
## T4 1.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## T ~~
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day1 ~~
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day2 ~~
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses1 ~~
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses2 ~~
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses3 ~~
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## E1 ~~
## E2 0.000
## E3 0.000
## E4 0.000
## E2 ~~
## E3 0.000
## E4 0.000
## E3 ~~
## E4 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .T1 -0.013 0.296 -0.044 0.965
## .T2 0.043 0.296 0.146 0.884
## .T3 0.122 0.296 0.411 0.681
## .T4 0.067 0.296 0.227 0.821
## T 0.000
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## T (ltt1) 7.985 1.174 6.798 0.000
## day1 (ltd1) 0.407 0.098 4.172 0.000
## day2 (ltd1) 0.407 0.098 4.172 0.000
## ses1 (lts1) 0.153 0.061 2.535 0.011
## ses2 (lts1) 0.153 0.061 2.535 0.011
## ses3 (lts1) 0.153 0.061 2.535 0.011
## E1 (ltg1) 0.216 0.031 7.073 0.000
## E2 (ltg1) 0.216 0.031 7.073 0.000
## E3 (ltg1) 0.216 0.031 7.073 0.000
## E4 (ltg1) 0.216 0.031 7.073 0.000
## .T1 0.000
## .T2 0.000
## .T3 0.000
## .T4 0.000
##
##
## Group 2 [low]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## T =~
## T1 1.000
## T2 1.000
## T3 1.000
## T4 1.000
## day1 =~
## T1 1.000
## T2 1.000
## day2 =~
## T3 1.000
## T4 1.000
## ses1 =~
## T1 1.000
## T2 1.000
## ses2 =~
## T3 1.000
## ses3 =~
## T4 1.000
## E1 =~
## T1 1.000
## E2 =~
## T2 1.000
## E3 =~
## T3 1.000
## E4 =~
## T4 1.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## T ~~
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day1 ~~
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day2 ~~
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses1 ~~
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses2 ~~
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses3 ~~
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## E1 ~~
## E2 0.000
## E3 0.000
## E4 0.000
## E2 ~~
## E3 0.000
## E4 0.000
## E3 ~~
## E4 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .T1 0.056 0.180 0.310 0.757
## .T2 0.038 0.180 0.212 0.832
## .T3 0.035 0.180 0.191 0.848
## .T4 0.038 0.180 0.210 0.833
## T 0.000
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## T (ltt2) 2.639 0.407 6.488 0.000
## day1 (ltd2) 0.243 0.076 3.203 0.001
## day2 (ltd2) 0.243 0.076 3.203 0.001
## ses1 (lts2) 0.119 0.063 1.905 0.057
## ses2 (lts2) 0.119 0.063 1.905 0.057
## ses3 (lts2) 0.119 0.063 1.905 0.057
## E1 (ltg2) 0.250 0.035 7.081 0.000
## E2 (ltg2) 0.250 0.035 7.081 0.000
## E3 (ltg2) 0.250 0.035 7.081 0.000
## E4 (ltg2) 0.250 0.035 7.081 0.000
## .T1 0.000
## .T2 0.000
## .T3 0.000
## .T4 0.000
##
## Constraints:
## |Slack|
## lattimegroup1 - (0.0001) 7.985
## lattimegroup2 - (0.0001) 2.639
## latdaygroup1 - (0.0001) 0.407
## latdaygroup2 - (0.0001) 0.243
## latsessiongroup1 - (0.0001) 0.153
## latsessiongroup2 - (0.0001) 0.119
## lategroup1 - (0.0001) 0.216
## lategroup2 - (0.0001) 0.249
summary(m0)
## lavaan 0.6-8 ended normally after 434 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 28
## Number of inequality constraints 4
##
## Number of observations per group:
## high 100
## low 100
##
## Model Test User Model:
##
## Test statistic 45.492
## Degrees of freedom 16
## P-value (Chi-square) 0.000
## Test statistic for each group:
## high 17.723
## low 27.769
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
##
## Group 1 [high]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## T =~
## T1 1.000
## T2 1.000
## T3 1.000
## T4 1.000
## day1 =~
## T1 1.000
## T2 1.000
## day2 =~
## T3 1.000
## T4 1.000
## ses1 =~
## T1 1.000
## T2 1.000
## ses2 =~
## T3 1.000
## ses3 =~
## T4 1.000
## E1 =~
## T1 1.000
## E2 =~
## T2 1.000
## E3 =~
## T3 1.000
## E4 =~
## T4 1.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## T ~~
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day1 ~~
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day2 ~~
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses1 ~~
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses2 ~~
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses3 ~~
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## E1 ~~
## E2 0.000
## E3 0.000
## E4 0.000
## E2 ~~
## E3 0.000
## E4 0.000
## E3 ~~
## E4 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .T1 -0.013 0.245 -0.053 0.957
## .T2 0.043 0.245 0.176 0.860
## .T3 0.122 0.245 0.496 0.620
## .T4 0.067 0.245 0.274 0.784
## T 0.000
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## T (time) 5.312 0.559 9.503 0.000
## day1 (day) 0.326 0.061 5.327 0.000
## day2 (day) 0.326 0.061 5.327 0.000
## ses1 (sssn) 0.135 0.044 3.104 0.002
## ses2 (sssn) 0.135 0.044 3.104 0.002
## ses3 (sssn) 0.135 0.044 3.104 0.002
## E1 (e) 0.233 0.023 10.006 0.000
## E2 (e) 0.233 0.023 10.006 0.000
## E3 (e) 0.233 0.023 10.006 0.000
## E4 (e) 0.233 0.023 10.006 0.000
## .T1 0.000
## .T2 0.000
## .T3 0.000
## .T4 0.000
##
##
## Group 2 [low]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## T =~
## T1 1.000
## T2 1.000
## T3 1.000
## T4 1.000
## day1 =~
## T1 1.000
## T2 1.000
## day2 =~
## T3 1.000
## T4 1.000
## ses1 =~
## T1 1.000
## T2 1.000
## ses2 =~
## T3 1.000
## ses3 =~
## T4 1.000
## E1 =~
## T1 1.000
## E2 =~
## T2 1.000
## E3 =~
## T3 1.000
## E4 =~
## T4 1.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## T ~~
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day1 ~~
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## day2 ~~
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses1 ~~
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses2 ~~
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## ses3 ~~
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
## E1 ~~
## E2 0.000
## E3 0.000
## E4 0.000
## E2 ~~
## E3 0.000
## E4 0.000
## E3 ~~
## E4 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .T1 0.056 0.245 0.228 0.820
## .T2 0.038 0.245 0.156 0.876
## .T3 0.035 0.245 0.141 0.888
## .T4 0.038 0.245 0.155 0.877
## T 0.000
## day1 0.000
## day2 0.000
## ses1 0.000
## ses2 0.000
## ses3 0.000
## E1 0.000
## E2 0.000
## E3 0.000
## E4 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## T (time) 5.312 0.559 9.503 0.000
## day1 (day) 0.326 0.061 5.327 0.000
## day2 (day) 0.326 0.061 5.327 0.000
## ses1 (sssn) 0.135 0.044 3.104 0.002
## ses2 (sssn) 0.135 0.044 3.104 0.002
## ses3 (sssn) 0.135 0.044 3.104 0.002
## E1 (e) 0.233 0.023 10.006 0.000
## E2 (e) 0.233 0.023 10.006 0.000
## E3 (e) 0.233 0.023 10.006 0.000
## E4 (e) 0.233 0.023 10.006 0.000
## .T1 0.000
## .T2 0.000
## .T3 0.000
## .T4 0.000
##
## Constraints:
## |Slack|
## time - (0.0001) 5.312
## day - (0.0001) 0.326
## session - (0.0001) 0.135
## e - (0.0001) 0.233
anova(m1, m0)
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## m1 12 2419.8 2472.5 15.425
## m0 16 2441.8 2481.4 45.492 30.067 4 4.743e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1