Parameter Estimation of Item Response Theory with Estimation of Latent Distribution.

Welcome to IRTest!

Please feel free tocreate an issuefor bug reports or potential improvements.

• IRTest is a useful tool for $\mathcal{\color{red}{IRT}}$ (item response theory) parameter $\mathcal{\color{red}{est}}\textrm{imation}$, especially when the violation of normality assumption on latent distribution is suspected.

• IRTest deals with uni-dimensional latent variable.

• For missing values, IRTest adopts full information maximum likelihood (FIML) approach.

• In IRTest, including the conventional usage of Gaussian distribution, several methods are available for estimation of latent distribution:

  • empirical histogram method,
  • two-component Gaussian mixture distribution,
  • Davidian curve,
  • kernel density estimation,
  • log-linear smoothing.

Installation

The CRAN version of IRTest can be installed on R-console with:

install.packages("IRTest")

For the development version, it can be installed on R-console with:

devtools::install_github("SeewooLi/IRTest")

Functions

Followings are the functions of IRTest.

• IRTest_Dich is the estimation function when items are dichotomously scored.

• IRTest_Poly is the estimation function when items are polytomously scored.

• IRTest_Cont is the estimation function when items are continuously scored.

• IRTest_Mix is the estimation function for a mixed-format test, a test comprising both dichotomous item(s) and polytomous item(s).

• factor_score estimates factor scores of examinees.

• coef_se returns standard errors of item parameter estimates.

• best_model selects the best model using an evaluation criterion.

• item_fit tests the statistical fit of all items individually.

• inform_f_item calculates the information value(s) of an item.

• inform_f_test calculates the information value(s) of a test.

• plot_item draws item response function(s) of an item.

• reliability calculates marginal reliability coefficient of IRT.

• latent_distribution returns evaluated PDF value(s) of an estimated latent distribution.

• DataGeneration generates several objects that can be useful for computer simulation studies. Among these are simulated item parameters, ability parameters and the corresponding item-response data.

• dist2 is a probability density function of two-component Gaussian mixture distribution.

• original_par_2GM converts re-parameterized parameters of two-component Gaussian mixture distribution into original parameters.

• cat_clps recommends category collapsing based on item parameters (or, equivalently, item response functions).

• recategorize implements the category collapsing.

• For S3 methods, anova, coef, logLik, plot, print, and summary are available.

Example

A simple simulation study for a 2PL model can be done in following manners:

library(IRTest)

• Data generation

An artificial data of 1000 examinees and 20 items.

Alldata <- DataGeneration(seed = 123456789,
                          model_D = 2,
                          N=1000,
                          nitem_D = 10,
                          latent_dist = "2NM",
                          m=0, # mean of the latent distribution
                          s=1, # s.d. of the latent distribution
                          d = 1.664,
                          sd_ratio = 2,
                          prob = 0.3)

data <- Alldata$data_D
item <- Alldata$item_D
theta <- Alldata$theta
colnames(data) <- paste0("item",1:10)

• Analysis

For an illustrative purpose, the two-component Gaussian mixture distribution (2NM) method is used for the estimation of latent distribution.

Mod1 <- 
  IRTest_Dich(
    data = data,
    latent_dist = "2NM"
    )

• Summary of the result

summary(Mod1)
#> Convergence:  
#> Successfully converged below the threshold of 1e-04 on 52nd iterations. 
#> 
#> Model Fit:  
#>  log-likeli   -4786.734 
#>    deviance   9573.469 
#>         AIC   9619.469 
#>         BIC   9732.347 
#>          HQ   9662.37 
#> 
#> The Number of Parameters:  
#>        item   20 
#>        dist   3 
#>       total   23 
#> 
#> The Number of Items:  10 
#> 
#> The Estimated Latent Distribution:  
#> method - 2NM 
#> ----------------------------------------
#>                                           
#>                                           
#>                                           
#>                       . @ @ .             
#>           .         . @ @ @ @ .           
#>         @ @ @ . . . @ @ @ @ @ @           
#>       @ @ @ @ @ @ @ @ @ @ @ @ @ @         
#>     . @ @ @ @ @ @ @ @ @ @ @ @ @ @ @       
#>     @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ .     
#>   @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @   
#> +---------+---------+---------+---------+
#> -2        -1        0         1         2

• Parameter estimation results

colnames(item) <- c("a", "b", "c")

knitr::kables(
  list(
    ### True item parameters 
    knitr::kable(item, format='simple', caption = "True item parameters", digits = 2)%>%
  kableExtra::kable_styling(font_size = 4),

    ### Estimated item parameters
    knitr::kable(coef(Mod1), format='simple', caption = "Estimated item parameters", digits = 2)%>%
  kableExtra::kable_styling(font_size = 4)
  )
)

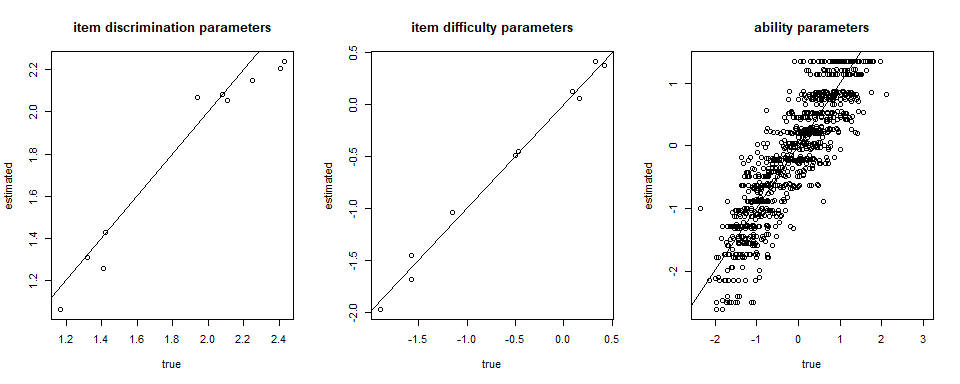
### Plotting
fscores <- factor_score(Mod1, ability_method = "MLE")

par(mfrow=c(1,3))
plot(item[,1], Mod1$par_est[,1], xlab = "true", ylab = "estimated", main = "item discrimination parameters")
abline(a=0,b=1)
plot(item[,2], Mod1$par_est[,2], xlab = "true", ylab = "estimated", main = "item difficulty parameters")
abline(a=0,b=1)
plot(theta, fscores$theta, xlab = "true", ylab = "estimated", main = "ability parameters")
abline(a=0,b=1)

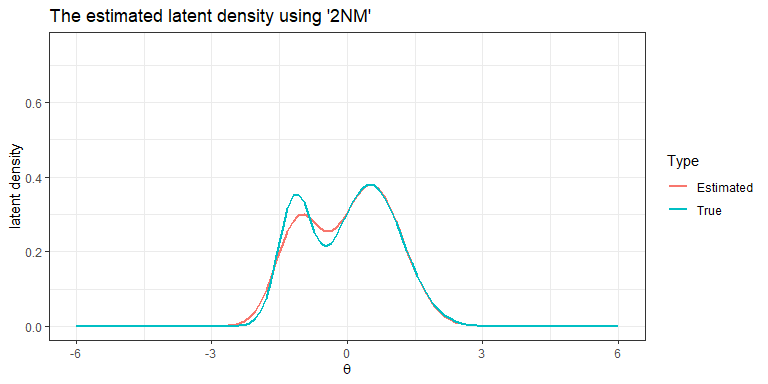
• The result of latent distribution estimation

plot(Mod1, mapping = aes(colour="Estimated"), linewidth = 1) +
  stat_function(
    fun = dist2,
    args = list(prob = .3, d = 1.664, sd_ratio = 2),
    mapping = aes(colour = "True"),
    linewidth = 1) +
  lims(y = c(0, .75)) + 
  labs(title="The estimated latent density using '2NM'", colour= "Type")+
  theme_bw()

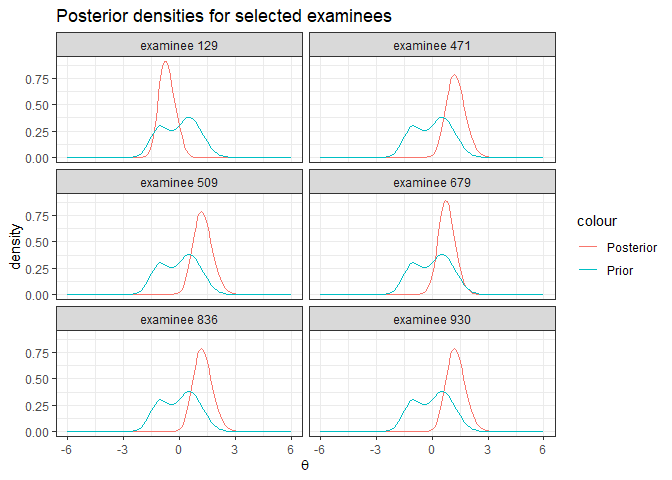
• Posterior distributions for the examinees

Each examinee’s posterior distribution is calculated in the E-step of EM algorithm. Posterior distributions can be found in Mod1$Pk.

set.seed(1)
selected_examinees <- sample(1:1000,6)
post_sample <- 
  data.frame(
    X = rep(seq(-6,6, length.out=121),6), 
    prior = rep(Mod1$Ak/(Mod1$quad[2]-Mod1$quad[1]), 6),
    posterior = 10*c(t(Mod1$Pk[selected_examinees,])), 
    ID = rep(paste("examinee", selected_examinees), each=121)
    )

ggplot(data=post_sample, mapping=aes(x=X))+
  geom_line(mapping=aes(y=posterior, group=ID, color='Posterior'))+
  geom_line(mapping=aes(y=prior, group=ID, color='Prior'))+
  labs(title="Posterior densities for selected examinees", x=expression(theta), y='density')+
  facet_wrap(~ID, ncol=2)+
  theme_bw()

• Item fit

item_fit(Mod1)
#>            stat df p.value
#> item1  21.05639  5  0.0008
#> item2  39.02560  5  0.0000
#> item3  18.38326  5  0.0025
#> item4  26.05405  5  0.0001
#> item5  14.32893  5  0.0136
#> item6  38.58140  5  0.0000
#> item7  25.55899  5  0.0001
#> item8  14.43694  5  0.0131
#> item9  18.29131  5  0.0026
#> item10 65.25700  5  0.0000

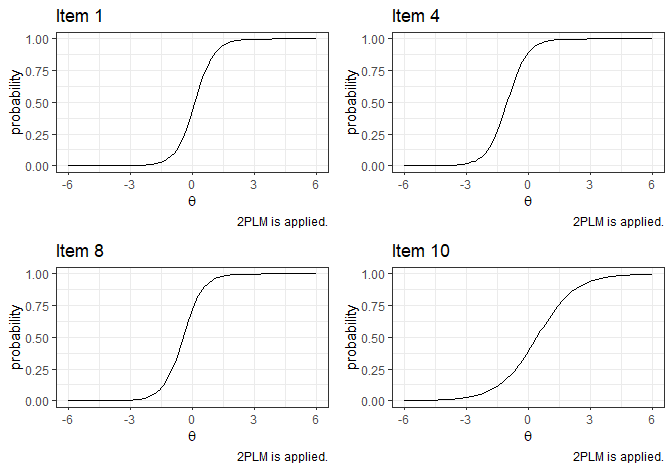
• Item response function

p1 <- plot_item(Mod1,1)
p2 <- plot_item(Mod1,4)
p3 <- plot_item(Mod1,8)
p4 <- plot_item(Mod1,10)
grid.arrange(p1, p2, p3, p4, ncol=2, nrow=2)

• Reliability

reliability(Mod1)
#> $summed.score.scale
#> $summed.score.scale$test
#> test reliability 
#>        0.8133725 
#> 
#> $summed.score.scale$item
#>     item1     item2     item3     item4     item5     item6     item7     item8 
#> 0.4586843 0.3014154 0.3020563 0.3805659 0.1425990 0.4534580 0.2688948 0.4475414 
#>     item9    item10 
#> 0.2661783 0.1963062 
#> 
#> 
#> $theta.scale
#> test reliability 
#>        0.7457047

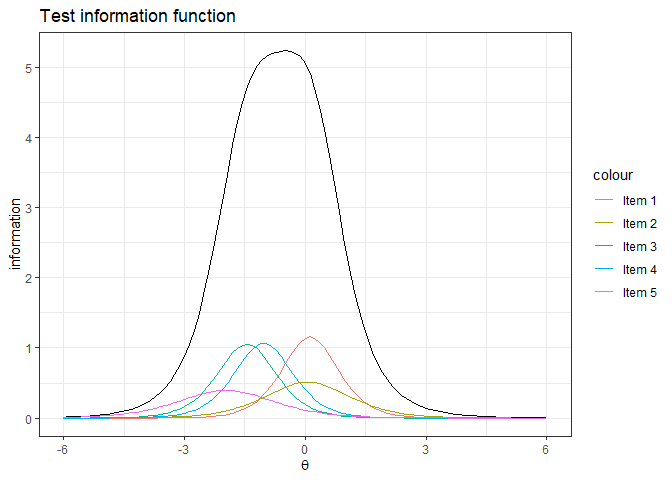
• Test information function

ggplot()+
  stat_function(
    fun = inform_f_test,
    args = list(Mod1)
  )+ 
  stat_function(
    fun=inform_f_item,
    args = list(Mod1, 1),
    mapping = aes(color="Item 1")
  )+
  stat_function(
    fun=inform_f_item,
    args = list(Mod1, 2),
    mapping = aes(color="Item 2")
  )+
  stat_function(
    fun=inform_f_item,
    args = list(Mod1, 3),
    mapping = aes(color="Item 3")
  )+
  stat_function(
    fun=inform_f_item,
    args = list(Mod1, 4),
    mapping = aes(color="Item 4")
  )+
  stat_function(
    fun=inform_f_item,
    args = list(Mod1, 5),
    mapping = aes(color="Item 5")
  )+
  lims(x=c(-6,6))+
  labs(title="Test information function", x=expression(theta), y='information')+
  theme_bw()