Receiver Operating Characteristic Based on Power Lindley Distribution.
PLindleyROC
The goal of PLindleyROC is to evaluate the Receiver Operating Characteristic (ROC) for Power Lindley Distribution. Additionally, The performace asssesments can be performed associated with the Bi-Power Lindley ROC model.
Installation
You can install the development version of PLindleyROC via the following code:
# install.packages("devtools")
devtools::install_github("ErtanSU/PLindleyROC")
Example
This is a basic example which shows you how to solve a common problem:
library(PLindleyROC)
dPLD(c(1,2,3,4,5,200),alpha=3,beta=2)
#> [1] 1.082682e+00 1.620507e-05 3.560890e-21 1.070039e-52 3.363180e-105
#> [6] 0.000000e+00
library(PLindleyROC)
pPLD(c(.5,1,2,3,4),alpha=3,beta=2)
#> [1] 0.1562992 0.7744412 0.9999993 1.0000000 1.0000000
library(PLindleyROC)
qPLD(c(.9971,0.5,0.3),alpha=3,beta=2)
#> [1] 1.5220612 0.7868721 0.6362570
library(PLindleyROC)
rPLD(10,alpha=3,beta=2)
#> [1] 0.2727832 1.2392219 0.7699234 0.4779818 0.8165381 0.4798310 0.9760771
#> [8] 1.1943763 0.7794092 1.1113773
library(PLindleyROC)
r.pl_auc(x=c(1,2,2,3,1),y=c(1,3,2,4,2,3),true_param=c(alpha1=1,beta1=1,alpha2=1,beta2=1),method=c("TRUE"))
#> [1] 0.5
library(PLindleyROC)
r.pl_index(x=c(1,2,2,3,1),y=c(1,3,2,4,2,3),init_param=c(1,1,1,1),init_index=1,method=c("MLE"))
#> Cut-off Point Sensitivity Specificity 1-Specificity
#> J 2.257651 0.5843951 0.7345488 0.2654512
#> ER 2.128638 0.6365278 0.6790223 0.3209777
#> CZ 2.155423 0.6258267 0.6909883 0.3090117
#> EC 2.049502 0.6676484 0.6424604 0.3575396
library(PLindleyROC)
x=c(1,2,2,3,1)
y=c(1,3,2,4,2,3)
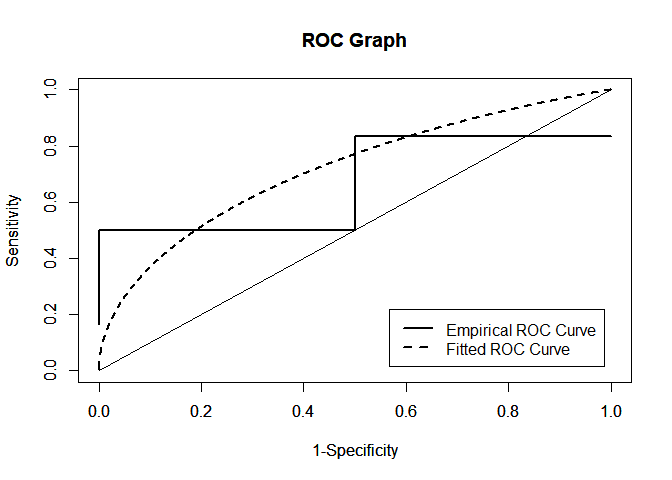
r.pl_graph(x,y,init_param=c(1,1,1,1),empirical=TRUE,method=c("MLE"))
Corresponding Author
Department of Statistics, Faculty of Science, Selcuk University, 42250, Konya, Turkey
Email:https://www.researchgate.net/profile/Ertan-Akgenc
References
Akgenç, E., and Kuş, C., 2023, ROC Curve Analysis for the Measurements Distributed Power-Lindley Distribution, 2nd International E-Conference On Mathematical And Statistical Sciences: A Selçuk Meeting (ICOMSS-2023), Konya, 25.
Attwood, K., Hou, S., and Hutson, A., 2022, Application of the skew exponential power distribution to ROC curves, Journal of Applied Statistics, 1-16.
Ghitany M., Al-Mutairi D. K., Balakrishnan N., and Al-Enezi L., 2013, Power lindley distribution and associated inference, Computational Statistics & Data Analysis, 64,20–33.
Liu, X., 2012, Classification accuracy and cut point selection, Statistics in medicine, 31(23), 2676-2686.
Nahm, F. S., 2022, Receiver operating characteristic curve: overview and practical use for clinicians, Korean journal of anesthesiology, 75(1), 25-36.
Perkins, N. J., and Schisterman, E. F., 2006, The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve, American journal of epidemiology, 163(7), 670-675.
Pundir, S. and Amala, R., 2014, Evaluation of area under the constant shape bi-weibull roc curve, Journal of Modern Applied Statistical Methods, 13(1),1-20.
Youden, W. J., 1950, Index for rating diagnostic tests, Cancer, 3(1), 32-35.