Validation of Estimates of Treatment Effects in Observational Data.

RCTrep: An R package for validation of methods for treatment effect estimation using real-world data

RCTrep is an R package to validate methods for conditional average treatment effect (CATE) estimation using real-world data (RWD). Validation of methods for treatment effect estimation using RWD is challenging because we do not observe the true treatment effect for each individual - a fundamental problem of causal inference - hence we can only estimate treatment effect using observed data. Randomized control trial (RCT) assigns individuals to treatment or control groups with known probability , hence two groups are balanced in terms of observed and unobserved covariates. The difference in outcomes between groups can be merely attributed to realization of treatment , and hence the treatment effect is the simple difference in means of outcomes and is unbiased given identification assumption holds. However, in case we don’t know the true probability in RWD, without knowing the ground truth, how can we validate the methods for treatment effect estimation?

Method

RCTrep is an R package to enable easy validation of various methods for treatment effect estimation using RWD by comparison to RCT data. We identify under which conditions the estimate from RCT can be regarded as the ground truth for methods validation using RWD. We assume the RWD and RCT data are two random samples from a, potentially different, population, and hence allow for a valid comparison of estimates of treatment effect between two samples after population composition is controlled for. We refer users to RCTrep vignettes for theoretical elaboration, in which we illustrate why estimates from RCT can be assumed as ground truth and how to use the estimates as the surrogate of the ground truth of RWD from the view of treatment assignment mechanism and sampling mechansim. We provide an diagram to show how RCT data and RWD differ in two mechanisms in the following figure:

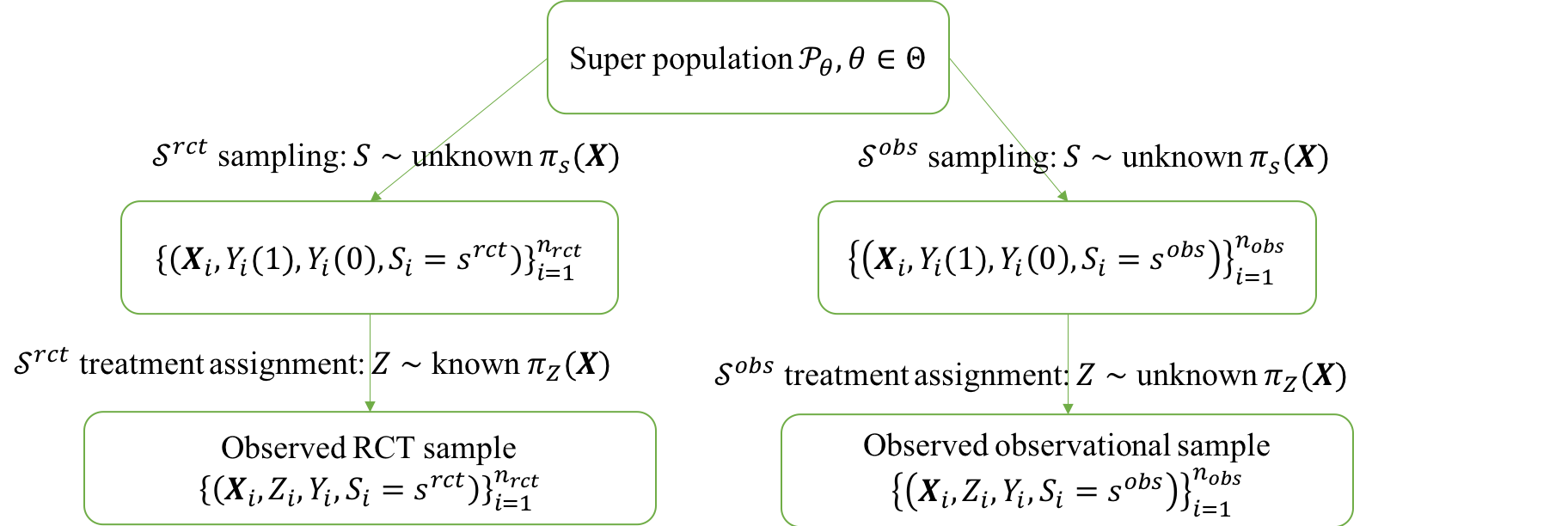
We consider a set of candidate treatment effect estimators , where , hence is an estimator of conditional average treatment effect of population with characteristics . We provide the package that makes it easy to try out various estimators and select the best one using the following evaluation metric:

where is an unbiased estimate of the average treatment effect derived from the RCT data, and are the empirical density of in RCT data and RWD, is a weight for individuals in RWD with characteristics . Hence the weighted distribution of covariates in RWD and distribution of covariates in the RCT data are balanced. We compute on population and sub-population levels.

Software overview

The package use R6 Object-oriented programming system. We provide an overview of implementation of RCTrep in the following figure:

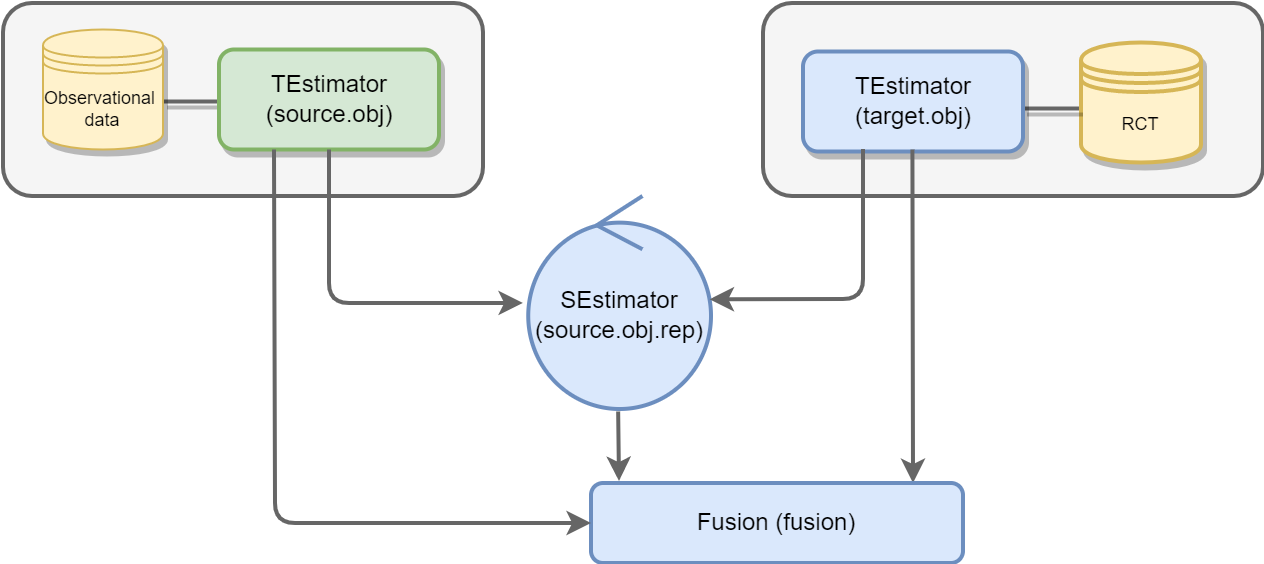
RCTrep provides two core classes, namely, TEstimator and SEstimator, which are responsible for adjusting the treatment assignment mechanism and the sampling mechanism respectively.

TEstimator has three subclasses for adjusting the treatment assignment mechanism, namely,

• G-computation,
• Inverse propensity score weighting,
• Doubly robust estimation

SEstimator has three subclasses for adjusting the sampling mechanism, namely,

• Exact matching,
• Inverse sampling score weighting,
• Subclassification

Users can specify modeling approaches for sampling score, propensity score, outcome regression, and distance measure, etc. Two objects instantiated using RWD and experimental RCT data communicate within the object of the class SEstimator, sharing either unit-level data” or aggregated data for computing the weights .

Summary R6 class Summary combines estimates from an object of class TEstimate and/or an object of class SEstimate, and plots and evaluates estimates of average treatment effect and heterogeneous treatment effect. The number of objects of class TEstimator or SEstimator passed to its constructor is not limited.

The package can also generate synthetic RCT data based on meta data from publications (point estimate and interval estimate of average treatment effect, conditional average treatment effect conditioning on univariate variable, and univariate distribution).

Installation

You can install the development version from GitHub with:

# install.packages("devtools")
devtools::install_github("duolajiang/RCTrep")

We will realease the package to CRAN soon.

Quick Start

We demonstrate the simple usage of RCTrep to validate methods for treatment effect estimation. We use G-computation to adjust for the treatment assignment mechanism - the method using RWD to validate. We use exact matching to balance covariates between RWD and RCT data, and obtain the weighted estimates of treatment effect using RWD. Then we can implement the fair comparison between weighted estimates using RWD and unbiased estimate using experimental data. Variables that may confound causal association between treatment and outcome, and variables that may lead to supurious association between sampling and outcomes still need careful investigation and identification.

Step 1: Identification

This step is to identify the variable set outcome_predictors that confound causal relation between treatment and outcome, and the variable set selection_predictors that can induce spurious difference in estimates between RWD and RCT data.

library(RCTrep)
source.data <- RCTrep::source.data
target.data <- RCTrep::target.data

vars_name <- list(outcome_predictors=c("x1","x2","x3","x4","x5","x6"),
                  treatment_name=c('z'),
                  outcome_name=c('y')
)
selection_predictors <- c("x1","x2","x3","x4","x5","x6")

Step 2: Estimation

step 2.1: Estimation of treatment effect of RWD and RCT data

source.obj <- TEstimator_wrapper(
  Estimator = "G_computation",
  data = source.data,
  name = "RWD",
  vars_name = vars_name,
  outcome_method = "glm",
  outcome_formula = y ~ x1 + x2 + x3 + z + z:x1 + z:x2 +z:x3+ z:x6,
  data.public = TRUE
)
#> y ~ x1 + x2 + x3 + z + z:x1 + z:x2 + z:x3 + z:x6

target.obj <- TEstimator_wrapper(
  Estimator = "Crude",
  data = target.data,
  name = "RCT",
  vars_name = vars_name,
  data.public = TRUE,
  isTrial = TRUE
)

Step 2.2: Estimation of weighted treatment effect of RWD

# step2.2: Estimation of weighted treatment effect
source.obj.rep <- SEstimator_wrapper(Estimator="Exact",
                                target.obj=target.obj,
                                source.obj=source.obj,
                                selection_predictors=selection_predictors)
source.obj.rep$EstimateRep(stratification = c("x1","x3","x4","x5"))

Step 3: Assumptions and model diagnosis

This step diagnoses model assumption for G-computation (covariats balance for IPW), treatment overlap assumption, outcome overlap assumption, and sampling overlap assumption.

source.obj$diagnosis_t_ignorability()
#> $residuals.overall
#> [1] 2.214633e-14
#> 
#> $residuals.subgroups
#>    x1 x2 x3 x4 x5 x6 sample.size     res.mean     res.se       msr       sesr
#> 1   0  0  0  0  0  0           8 -0.033159812 0.28630939 0.5749111 0.25909656
#> 2   0  0  0  0  0  1          31 -0.099669263 0.15500392 0.7307204 0.16986746
#> 3   0  0  0  0  1  0          16 -0.291784223 0.22392759 0.8372915 0.33709962
#> 4   0  0  0  0  1  1          68 -0.081493792 0.10890826 0.8013288 0.12627815
#> 5   0  0  0  1  0  0          29  0.289766947 0.18601148 1.0527725 0.28109093
#> 6   0  0  0  1  0  1         122 -0.018623426 0.09563139 1.1069356 0.10495348
#> 7   0  0  0  1  1  1         297 -0.039424153 0.05472699 0.8880872 0.07021318
#> 8   0  0  1  0  0  0          27  0.359416934 0.23566150 1.5731255 0.27345679
#> 9   0  0  1  0  0  1         116 -0.064430174 0.10341172 1.2339593 0.14397971
#> 10  0  0  1  0  1  0          73  0.122384056 0.11547447 0.9750512 0.17221696
#> 11  0  0  1  1  0  0         140 -0.103108837 0.08108053 0.9244247 0.09551924
#> 12  0  0  1  1  1  0         259  0.042947650 0.06087029 0.9577841 0.09134774
#> 13  0  1  0  0  0  1           7 -0.536943485 0.34724241 1.0117720 0.69268561
#> 14  0  1  0  0  1  0           5 -0.138659594 0.21350193 0.2015588 0.10876393
#> 15  0  1  0  0  1  1          16 -0.044121152 0.27092416 1.1029452 0.37762497
#> 16  0  1  0  1  0  1          33 -0.029399192 0.16582744 0.8808240 0.32867335
#> 17  0  1  0  1  1  0          15  0.225047363 0.28999923 1.2280401 0.50759032
#> 18  0  1  0  1  1  1          79  0.111122348 0.11518856 1.0472837 0.14102420
#> 19  0  1  1  0  0  0          10 -0.489153001 0.28166251 0.9532746 0.23392786
#> 20  0  1  1  0  0  1          28  0.043123603 0.20235159 1.1074062 0.29713360
#> 21  0  1  1  0  1  0          19  0.003265044 0.27119153 1.3238179 0.31297388
#> 22  0  1  1  0  1  1          72  0.002178221 0.10858861 0.8372002 0.15777598
#> 23  0  1  1  1  0  0          35  0.170865832 0.13459768 0.6451573 0.14548423
#> 24  0  1  1  1  0  1         125 -0.056121898 0.09058246 1.0205923 0.15850343
#> 25  0  1  1  1  1  0          65  0.040177469 0.12293937 0.9689158 0.23001168
#> 26  0  1  1  1  1  1         296  0.024164125 0.05184835 0.7936179 0.06180646
#> 27  1  0  0  0  0  0           2  1.020056964 1.04248503 2.1272913 2.12678823
#> 28  1  0  0  0  1  0           4  0.590859805 0.43729538 0.9227971 0.51590407
#> 29  1  0  0  0  1  1          22 -0.027696594 0.18169792 0.6940639 0.14754895
#> 30  1  0  0  1  0  0          11  0.249437181 0.31263135 1.0396025 0.31885782
#> 31  1  0  0  1  0  1          36  0.220385980 0.17795769 1.1569829 0.19544718
#> 32  1  0  0  1  1  0          16  0.048570074 0.19875700 0.5949242 0.15698698
#> 33  1  0  1  0  0  0           9  0.197302831 0.31820751 0.8489766 0.40225460
#> 34  1  0  1  0  0  1          32 -0.045410644 0.18378995 1.0492033 0.18998055
#> 35  1  0  1  0  1  0          19  0.092662797 0.25283001 1.1592007 0.44746032
#> 36  1  0  1  0  1  1          71  0.043913387 0.12107083 1.0279986 0.16060356
#> 37  1  0  1  1  0  0          32  0.179626509 0.14713726 0.7033962 0.15161745
#> 38  1  0  1  1  0  1         121 -0.118212578 0.08039760 0.7896270 0.09712507
#> 39  1  0  1  1  1  0          67 -0.009015888 0.13323385 1.1716644 0.21134724
#> 40  1  1  0  0  0  1           3 -0.801041824 0.30720451 0.8304172 0.58650330
#> 41  1  1  0  1  0  0           2  0.116839187 0.44234613 0.2093215 0.10336672
#> 42  1  1  0  1  0  1           9  0.061176434 0.40000603 1.2837812 0.60733013
#> 43  1  1  0  1  1  0           4  0.023281191 0.34205505 0.3515470 0.20537435
#> 44  1  1  0  1  1  1          20 -0.030336997 0.26684840 1.3538736 0.39312787
#> 45  1  1  1  0  0  1          12  0.002671423 0.15873990 0.2771891 0.11673024
#> 46  1  1  1  0  1  0           5 -0.260903445 0.54680276 1.2640436 0.56667606
#> 47  1  1  1  0  1  1          14 -0.231240962 0.30847904 1.2905435 0.36617811
#> 48  1  1  1  1  0  0           8  0.062835422 0.18528567 0.2442638 0.11057093
#> 49  1  1  1  1  0  1          32  0.193141574 0.15858574 0.8169362 0.24339579
#> 50  1  1  1  1  1  0           9 -0.024257039 0.20129750 0.3247539 0.14474685
#> 51  1  1  1  1  1  1          71 -0.156520230 0.10575745 0.8074232 0.12569119
#> 
#> $plot.res.mse

source.obj$diagnosis_t_overlap()

source.obj.rep$diagnosis_s_ignorability()
#> to be continued... This function is to check if
#>               confounders_sampling are balanced between source and target object
#>               on population and sub-population levels stratified by
#>               stratificaiton and stratification_joint.

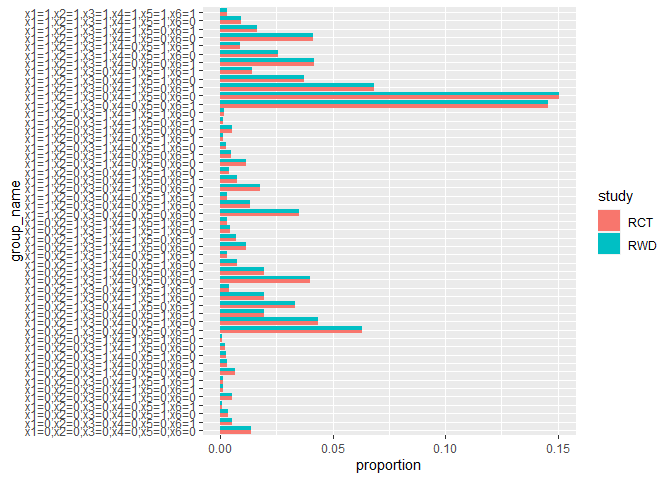
source.obj.rep$diagnosis_s_overlap()

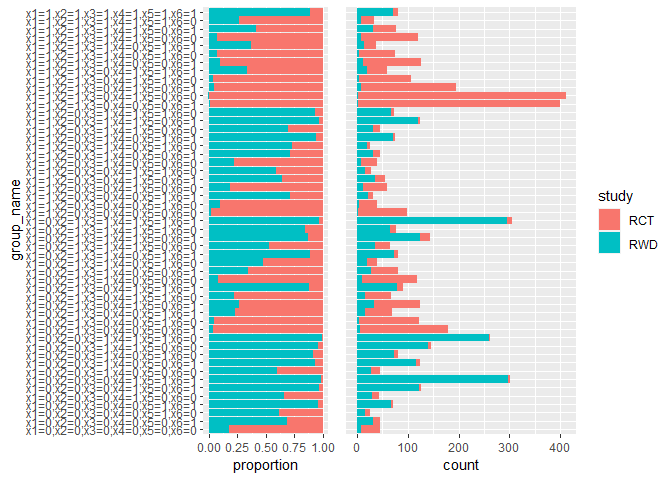
Step 4: Model Validation

This step compare the estimates from RWD with those from RCT data, and validate difference methods using RWD.

fusion <- Fusion$new(target.obj,
                     source.obj,
                     source.obj.rep)
fusion$evaluate()
#> # A tibble: 34 x 7
#> # Groups:   group_name [17]
#>    group_name          estimator             size     mse len_ci agg.est agg.reg
#>    <chr>               <chr>                <dbl>   <dbl>  <dbl> <lgl>   <lgl>  
#>  1 pop                 G_computation/glm/E~  2622 9.8 e-2  4.83  TRUE    TRUE   
#>  2 pop                 G_computation/glm     2622 6.66e+2  0.239 FALSE   TRUE   
#>  3 x1=0,x3=0,x4=0,x5=0 G_computation/glm/E~    46 5.58e+0  9.53  TRUE    TRUE   
#>  4 x1=0,x3=0,x4=0,x5=0 G_computation/glm       46 1.58e+3  1.33  FALSE   TRUE   
#>  5 x1=0,x3=0,x4=0,x5=1 G_computation/glm/E~   105 3.55e+0  8.94  TRUE    TRUE   
#>  6 x1=0,x3=0,x4=0,x5=1 G_computation/glm      105 1.35e+3  0.938 FALSE   TRUE   
#>  7 x1=0,x3=0,x4=1,x5=0 G_computation/glm/E~   184 1.21e+1  4.64  TRUE    TRUE   
#>  8 x1=0,x3=0,x4=1,x5=0 G_computation/glm      184 1.28e+3  0.707 FALSE   TRUE   
#>  9 x1=0,x3=0,x4=1,x5=1 G_computation/glm/E~   391 9.47e+0  6.21  TRUE    TRUE   
#> 10 x1=0,x3=0,x4=1,x5=1 G_computation/glm      391 9.68e+2  0.502 FALSE   TRUE   
#> # i 24 more rows
fusion$plot()