Simple and Fast ROC Curves.

ROCket

Intro

ROCket was primarily build for ROC curve estimation in the presence of aggregated data. Nevertheless, it can also handle raw samples. In general, aggregating data can be very beneficial when dealing with large datasets. Whenever a dataset consists of categorical or discretized continuous features, the data size can be effectively reduced by calculating sufficient statistics for each constellation of feature values. This saves memory and reduces the time needed to train classification models. Also model accuracy assessment can be done on aggregated data, which yields similar benefits. To this end, ROCket provides functions for ROC curve estimation and AUC calculation.

Installation

# From CRAN
install.packages("ROCket")

# From GitHub
# install.packages("devtools")
devtools::install_github("da-zar/ROCket")

Example

Data preparation

The easiest way to get started is to prepare a dataset containing all distinct predicted score values together with their count and the number of positive cases. Your dataset could look like this:

nrow(data_agg)
#> [1] 11
head(data_agg)
#>    score totals positives
#> 1:     1  62840     38499
#> 2:     0  62309     23985
#> 3:     2  30143     24092
#> 4:    -1  30282      6072
#> 5:    -2   6509       597
#> 6:     3   6642      6082

You can now pass this data to the rkt_prep function in order to create an object that will be later used for estimating ROC curves (possibly with several different algorithms).

prep_data_agg <- rkt_prep(
  scores = data_agg$score, 
  positives = data_agg$positives, 
  totals = data_agg$totals
)

It is not necessary to use an aggregated dataset. It’s also possible to have each single observation in a separate row – in this case the positives argument is the regular indicator (a numeric vector is required) for positive observations and the totals argument is not needed anymore (default is 1).

You can print the object, to get some information about the content, or plot it:

prep_data_agg
#> .:: ROCket Prep Object 
#> Positives (pos_n): 100000 
#> Negatives (neg_n): 100000 
#> Pos ECDF (pos_ecdf): rkt_ecdf function 
#> Neg ECDF (neg_ecdf): rkt_ecdf function
plot(prep_data_agg)

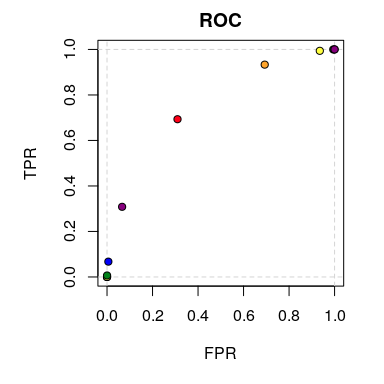
ROC curves

Estimates of the ROC curve can be calculated with the rkt_roc function. It takes two arguments. The first one is the rkt_prep object, which contains all the needed data, and the second one is an integer saying which method of estimation should be used. A list of implemented methods can be retrieved with the show_methods function.

show_methods()
#>    nr                            desc
#> 1:  1           ROC Curve (empirical)
#> 2:  2        ROC Function (empirical)
#> 3:  3 ROC Function (placement values)
#> 4:  4         ROC Function (binormal)

In ROCket, we distinguish two types of ROC curve representations:

1. parametric curves – TPR and FPR are functions of a parameter (the score),
2. functions – TPR is a function of FPR.

In the first case we estimate two functions, the x and y coordinates of the ROC curve (FPR, TPR). These two functions are returned as a list. In the second case the output is a regular function.

Let’s now calculate estimates of the ROC curve using all available methods.

roc_list <- list()
for (i in 1:4){
  roc_list[[i]] <- rkt_roc(prep_data_agg, method = i)
}

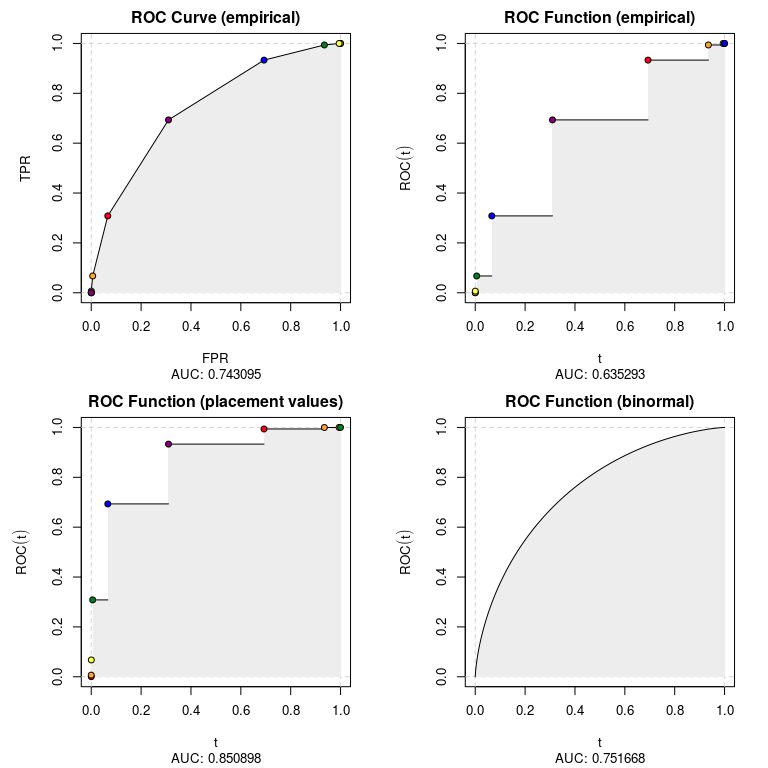
The output of rkt_roc can be used to plot the ROC curve estimates and calculate the AUC.

par(mfrow = c(2, 2))
for (i in 1:4){
  plot(
    roc_list[[i]], 
    main = show_methods()[i, desc], 
    sub = sprintf('AUC: %f', auc(roc_list[[i]]))
  )
}