Description
Measuring Information Flow Between Time Series with Shannon and Renyi Transfer Entropy.
Description
Measuring information flow between time series with Shannon and Rényi transfer entropy. See also Dimpfl and Peter (2013) <doi:10.1515/snde-2012-0044> and Dimpfl and Peter (2014) <doi:10.1016/j.intfin.2014.03.004> for theory and applications to financial time series. Additional references can be found in the theory part of the vignette.
README.md
RTransferEntropy
The goal of RTransferEntropy is to implement the calculation of the transfer entropy metric using Shannon’s or the Renyi’s methodology.
A short introduction can be found below, for a more thorough introduction to the transfer entropy methodology and the RTransferEntropy package, see the vignette and the RTransferEntropy paper. If you use the package in academic work, please make sure to cite us, see also citation("RTransferEntropy").
The authors of the TransferEntropy package no longer develop their package, which is deprecated as of 2018-08-10, and recommend the use of this package.
Installation
You can install RTransferEntropy with
install.packages("RTransferEntropy")
or the development version from github with
# install.packages("devtools")
devtools::install_github("BZPaper/RTransferEntropy")
Example using simulated data
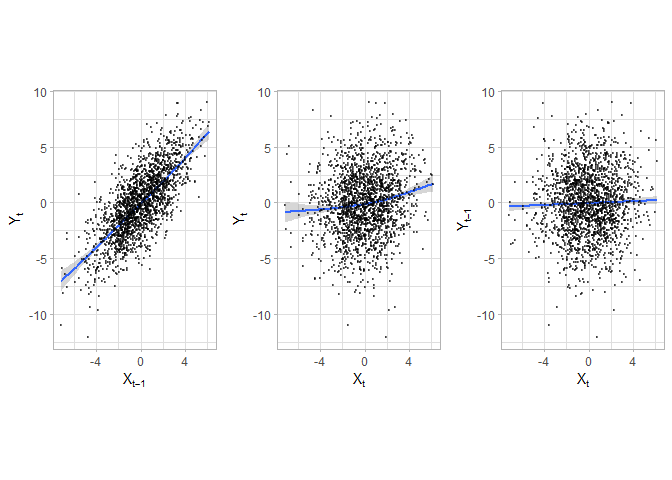
Simulate a simple model to obtain two time series that are not independent (see simulation study in Dimpfl and Peter (2013)), i.e. one time series is lag of the other plus noise. In this case, one expects significant information flow from x to y and none from y to x.
Simulating a Time-Series
library(RTransferEntropy)
library(future)
# enable parallel processing
plan(multisession)
set.seed(20180108)
n <- 2000
x <- rep(0, n + 1)
y <- rep(0, n + 1)
for (i in seq(n)) {
x[i + 1] <- 0.2 * x[i] + rnorm(1, 0, 2)
y[i + 1] <- x[i] + rnorm(1, 0, 2)
}
x <- x[-1]
y <- y[-1]
Visualisation
library(ggplot2)
library(gridExtra)
theme_set(theme_light())
# Lagged X-Plot
p1 <- ggplot(data.frame(x = c(NA, x[1:(length(x) - 1)]), y = y), aes(x, y)) +
geom_smooth() +
geom_point(alpha = 0.5, size = 0.5) +
labs(x = expression(X[t - 1]), y = expression(Y[t])) +
coord_fixed(1) +
scale_x_continuous(limits = range(x)) +
scale_y_continuous(limits = range(y))
# X-Y Plot
p2 <- ggplot(data.frame(x = x, y = y), aes(x, y)) +
geom_smooth() +
geom_point(alpha = 0.5, size = 0.5) +
labs(x = expression(X[t]), y = expression(Y[t])) +
coord_fixed(1) +
scale_x_continuous(limits = range(x)) +
scale_y_continuous(limits = range(y))
# Lagged Y Plot
p3 <- ggplot(data.frame(x = x, y = c(NA, y[1:(length(y) - 1)])), aes(x, y)) +
geom_smooth() +
geom_point(alpha = 0.5, size = 0.5) +
labs(x = expression(X[t]), y = expression(Y[t - 1])) +
coord_fixed(1) +
scale_x_continuous(limits = range(x)) +
scale_y_continuous(limits = range(y))
a <- grid.arrange(p1, p2, p3, ncol = 3)
Shannon Transfer Entropy
set.seed(20180108 + 1)
shannon_te <- transfer_entropy(x = x, y = y)
#> Shannon's entropy on 8 cores with 100 shuffles.
#> x and y have length 2000 (0 NAs removed)
#> [calculate] X->Y transfer entropy
#> [calculate] Y->X transfer entropy
#> [bootstrap] 300 times
#> Done - Total time 4.2 seconds
shannon_te
#> Shannon Transfer Entropy Results:
#> -----------------------------------------------------------
#> Direction TE Eff. TE Std.Err. p-value sig
#> -----------------------------------------------------------
#> X->Y 0.1245 0.1210 0.0014 0.0000 ***
#> Y->X 0.0020 0.0000 0.0014 0.8467
#> -----------------------------------------------------------
#> Bootstrapped TE Quantiles (300 replications):
#> -----------------------------------------------------------
#> Direction 0% 25% 50% 75% 100%
#> -----------------------------------------------------------
#> X->Y 0.0005 0.0022 0.0029 0.0040 0.0083
#> Y->X 0.0008 0.0024 0.0031 0.0041 0.0088
#> -----------------------------------------------------------
#> Number of Observations: 2000
#> -----------------------------------------------------------
#> p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.'
summary(shannon_te)
#> Shannon's Transfer Entropy
#>
#> Coefficients:
#> te ete se p-value
#> X->Y 0.1244709 0.1210119 0.0014 <2e-16 ***
#> Y->X 0.0020383 0.0000000 0.0014 0.8467
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Bootstrapped TE Quantiles (300 replications):
#> Direction 0% 25% 50% 75% 100%
#> X->Y 0.0005 0.0022 0.0029 0.0040 0.0083
#> Y->X 0.0008 0.0024 0.0031 0.0041 0.0088
#>
#> Number of Observations: 2000
Alternatively, you can calculate only the transfer entropy or the effective transfer entropy with
calc_te(x, y)
#> [1] 0.1244709
calc_te(y, x)
#> [1] 0.002038284
calc_ete(x, y)
#> [1] 0.1213265
calc_ete(y, x)
#> [1] 0
Renyi Transfer Entropy
set.seed(20180108 + 1)
renyi_te <- transfer_entropy(x = x, y = y, entropy = "renyi", q = 0.5)
#> Renyi's entropy on 8 cores with 100 shuffles.
#> x and y have length 2000 (0 NAs removed)
#> [calculate] X->Y transfer entropy
#> [calculate] Y->X transfer entropy
#> [bootstrap] 300 times
#> Done - Total time 3.62 seconds
renyi_te
#> Renyi Transfer Entropy Results:
#> -----------------------------------------------------------
#> Direction TE Eff. TE Std.Err. p-value sig
#> -----------------------------------------------------------
#> X->Y 0.0852 0.0393 0.0217 0.0300 *
#> Y->X 0.0276 -0.0139 0.0226 0.7233
#> -----------------------------------------------------------
#> Bootstrapped TE Quantiles (300 replications):
#> -----------------------------------------------------------
#> Direction 0% 25% 50% 75% 100%
#> -----------------------------------------------------------
#> X->Y -0.0094 0.0273 0.0404 0.0557 0.1132
#> Y->X -0.0358 0.0266 0.0421 0.0576 0.1141
#> -----------------------------------------------------------
#> Number of Observations: 2000
#> Q: 0.5
#> -----------------------------------------------------------
#> p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.'
calc_te(x, y, entropy = "renyi", q = 0.5)
#> [1] 0.08515726
calc_te(y, x, entropy = "renyi", q = 0.5)
#> [1] 0.02758021
calc_ete(x, y, entropy = "renyi", q = 0.5)
#> [1] 0.04393078
calc_ete(y, x, entropy = "renyi", q = 0.5)
#> [1] -0.01612456
Function Verbosity aka quiet = TRUE
To disable the verbosity of a function you can use the argument quiet. Note that we have set nboot = 0 as we don’t need bootstrapped quantiles for this example.
te <- transfer_entropy(x, y, nboot = 0, quiet = T)
te
#> Shannon Transfer Entropy Results:
#> -----------------------------------------------------------
#> Direction TE Eff. TE Std.Err. p-value sig
#> -----------------------------------------------------------
#> X->Y 0.1245 0.1212 NA NA
#> Y->X 0.0020 0.0000 NA NA
#> -----------------------------------------------------------
#> For calculation of standard errors and p-values set nboot > 0
#> -----------------------------------------------------------
#> Number of Observations: 2000
#> -----------------------------------------------------------
#> p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.'
If you want to disable feedback from transfer_entropy functions, you can do so by using set_quiet(TRUE)
set_quiet(TRUE)
te <- transfer_entropy(x, y, nboot = 0)
te
#> Shannon Transfer Entropy Results:
#> -----------------------------------------------------------
#> Direction TE Eff. TE Std.Err. p-value sig
#> -----------------------------------------------------------
#> X->Y 0.1245 0.1211 NA NA
#> Y->X 0.0020 0.0000 NA NA
#> -----------------------------------------------------------
#> For calculation of standard errors and p-values set nboot > 0
#> -----------------------------------------------------------
#> Number of Observations: 2000
#> -----------------------------------------------------------
#> p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.'
# revert back with
set_quiet(FALSE)
te <- transfer_entropy(x, y, nboot = 0)
#> Shannon's entropy on 8 cores with 100 shuffles.
#> x and y have length 2000 (0 NAs removed)
#> [calculate] X->Y transfer entropy
#> [calculate] Y->X transfer entropy
#> Done - Total time 0.13 seconds
Parallel Programming
Using the future package and its plans we can execute all computations in parallel like so
library(future)
plan(multisession)
te <- transfer_entropy(x, y, nboot = 100)
#> Shannon's entropy on 8 cores with 100 shuffles.
#> x and y have length 2000 (0 NAs removed)
#> [calculate] X->Y transfer entropy
#> [calculate] Y->X transfer entropy
#> [bootstrap] 100 times
#> Done - Total time 1.92 seconds
# revert to sequential mode
plan(sequential)
te <- transfer_entropy(x, y, nboot = 100)
#> Shannon's entropy on 1 core with 100 shuffles.
#> x and y have length 2000 (0 NAs removed)
#> [calculate] X->Y transfer entropy
#> [calculate] Y->X transfer entropy
#> [bootstrap] 100 times
#> Done - Total time 4.08 seconds
# close multisession, see also ?plan
plan(sequential)