Robust Outliers Detection.
# Routliers
Routliers is designed to help researchers to detect univariate and multivariate outliers, using robust methods: - The MAD method for detecting univariate outliers (see Leys et al. 2013) - The MMCD method for detecting multivariate outliers (see Leys et al. 2018) - The Mahalanobis distance method for detecting multivariate outliers is also available in order to facilite comparisons with the MMCD method. However, this method is less robust than the MMCD method and should be avoided.
Different functions are available in order to (a) detect univariate and multivariate outliers (b) plot univariate and multivariate outliers.
Installation
Currently, this package exists in a development version on GitHub. To use the package, you need to install it directly from GitHub using the install_github function from devtools.
You can use the following code to install the development version of Routliers:
library(devtools)
install_github("mdelacre/Routliers")
As a note, one of the dependencies in Routliers (i.e. MASS) have its own dependencies. You may be prompted to install additional packages to be able to install Routliers.
Examples of using the package
The Routliers package allows you to easily count, detect and plot outliers using robust methods. The most important functions in the package are outliers_mad and outliers_mcd, which allow to detect univariate and multivariate outliers, respectively. By default, the MAD function assume a normal distribution underlying the data and treat all value more than 3 MAD around the median as outliers. Moreover, the MCD function select by default h = n/2 observations on which the empirical mean and empirical covariance matrix are calculated (see Leys et al., 2018).
Here is an example of detecting extreme level of anxiety and depression (based on the HSCL-25; Derogatis, Lipman, Rickels, Uhlenhuth & Covi, 1974) in a sample of 2077 participants after the Brussels attacks, using the outliers_mad function. The 10 first items of the HSCL-25 are averaged in order to compute the level of anxiety and the 15 last items of the HSCL-25 are averaged in order to compute the level of depression. The MAD function is applied on the averaged scores.
data(Attacks)
anxiety <- rowMeans(
Attacks[,c("hsc1","hsc2","hsc3","hsc4",
"hsc5","hsc6","hsc7","hsc8","hsc9","hsc10")]
)
res1 <- outliers_mad(x = anxiety)
res1
#> Call:
#> outliers_mad.default(x = anxiety)
#>
#> Median:
#> [1] 1.7
#>
#> MAD:
#> [1] 0.59304
#>
#> Limits of acceptable range of values:
#> [1] -0.07912 3.47912
#>
#> Number of detected outliers
#> extremely low extremely high total
#> 0 25 25
depression <- rowMeans(
Attacks[,c("hsc11","hsc12","hsc13","hsc14",
"hsc15","hsc16","hsc17","hsc18",
"hsc19","hsc20","hsc21","hsc22",
"hsc23","hsc24","hsc25")]
)
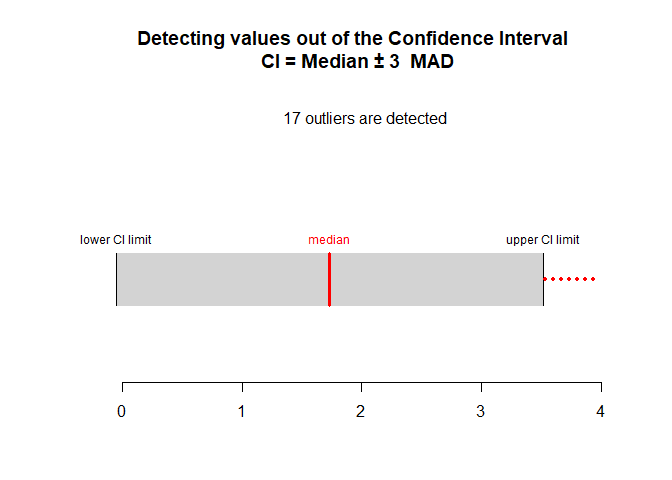
res2 <- outliers_mad(x = depression)
res2
#> Call:
#> outliers_mad.default(x = depression)
#>
#> Median:
#> [1] 1.733333
#>
#> MAD:
#> [1] 0.59304
#>
#> Limits of acceptable range of values:
#> [1] -0.04578667 3.51245333
#>
#> Number of detected outliers
#> extremely low extremely high total
#> 0 17 17
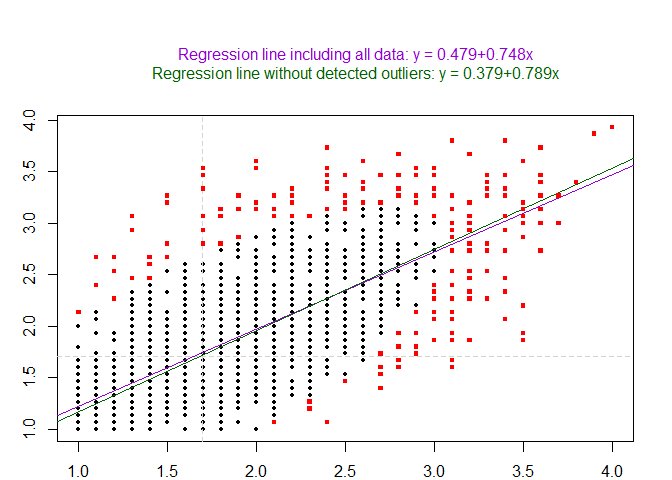
Here is an example of detecting extremely surprising combination of scores of anxiety and depression, using the outliers_mcd function.
resMCD <- outliers_mcd(x = data.frame(anxiety,depression))
resMCD
#> Call:
#> outliers_mcd.default(x = data.frame(anxiety, depression))
#>
#> Limit distance of acceptable values from the centroid :
#> [1] 9.21034
#>
#> Number of detected outliers:
#> total
#> 214
It is also possible to plot the outliers, using plot_outliers_mad and plot_outliers_mcd functions:
plot_outliers_mad(res2, x = depression)
the plot function for the mcd method is very useful as it allows to compare the regression line with and without outliers (showing if there is a strong impact of outliers on the regression line):
plot_outliers_mcd(resMCD, x = data.frame(anxiety,depression))