Computing Statistically-Equivalent Path Models.

SEset

An R package implementing the SE-set algorithm, a tool to explore statistically-equivalent path models from correlation matrices and Gaussian Graphical Models (GGMs).

Background

This repository contains an R package used by Ryan, Bringmann and Schuurman (pre-print)[PsyArXiv] to aid researchers in investigating the relationship between a given GGM estimate (in the form of a precision matrix) and possible underlying linear path models. Linear path models can also be interpreted as "weighted DAGs". Full details on the package can be found in Appendix B of the manuscript, and code to reproduce the empirical illustration in that paper can be found in this repository.

Please note that we recommend the use of this tool only for GGMs with 13 or less nodes as the size of the outputted object, and the run-time, grows factorialy ($p!$) with each node in the network.

Installation

The current version of this package can be installed directly from github using

devtools::install_github("ryanoisin/SEset")

Usage

The main SE-set function takes a precision matrix as input by default (but can also take a matrix of partial correlations, or a covariance matrix, detailed below). This can be estimated using packages such as qgraph, using either raw data or a matrix of correlations. For example, using the riskcor correlation matrix supplied with the package as input, the precision matrix omega can be estimated by running

# load data
data(riskcor)

# estimate precision matrix
estimate <- qgraph::EBICglasso(riskcor, n = 69, returnAllResults = TRUE)
omega <- estimate$optwi

# The precision matrix can also be standardized to a partial correlation matrix, and plotted as a network
library(qgraph)
parcor <- qgraph::wi2net(omega)
pnet <- qgraph(parcor, repulsion = .8,vsize = c(10,15), theme = "colorblind", fade = F, edge.labels = TRUE)

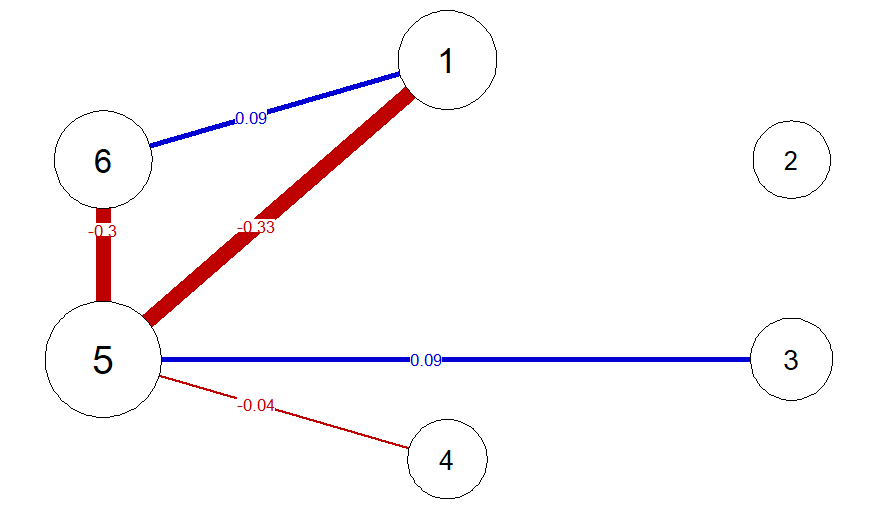
Given a $p$-variate precision matrix, the SEset package can be used to obtain a set of maximally $p!$ statistically equivalent weighted DAGs (i.e., linear path models): One DAG for every possible topological ordering of the $p$ variables, from exogenous to endogenous. This is the SE-set of omega which gives the package its name.

The statistically-equivalent set is found by using the network_to_SEset function

SE_example <- network_to_SEset(omega, digits = 2, rm_duplicates = TRUE)

where the digits arguments determines the rounding of parameters in the weighted DAGs, and the rm_duplicates argument indicates that only unique weighted DAGs should be returned: duplicates are removed after rounding. Typically, when duplicates are removed, the number of unique DAGs returned is much less than $p!$.

Exploring the SE-set

Individual members of the SE-set can be plotted, for example using qgraph. When visualizing, remember that the weights matrix of the path model $B$ is given in SEM form $X = BX +e$, and so should be read "from column to row", that is $b_{ij}$ encodes the direct effect of $X_j$ on $X_i$. As a consequence, matrices should be transposed when being used as input to qgraph and most other network visualization tools.

DAG1 <- matrix(SE_example[1,],6,6)
DAG2 <- matrix(SE_example[30,],6,6)

par(mfrow=c(1,2))
qgraph(t(DAG1), repulsion = .8,vsize = c(10,15), theme = "colorblind", fade = F,
        layout = pnet$layout, maximum = 2, edge.labels = T)
qgraph(t(DAG2), repulsion = .8,vsize = c(10,15), theme = "colorblind", fade = F,
        layout = pnet$layout, maximum = 2, edge.labels = T)

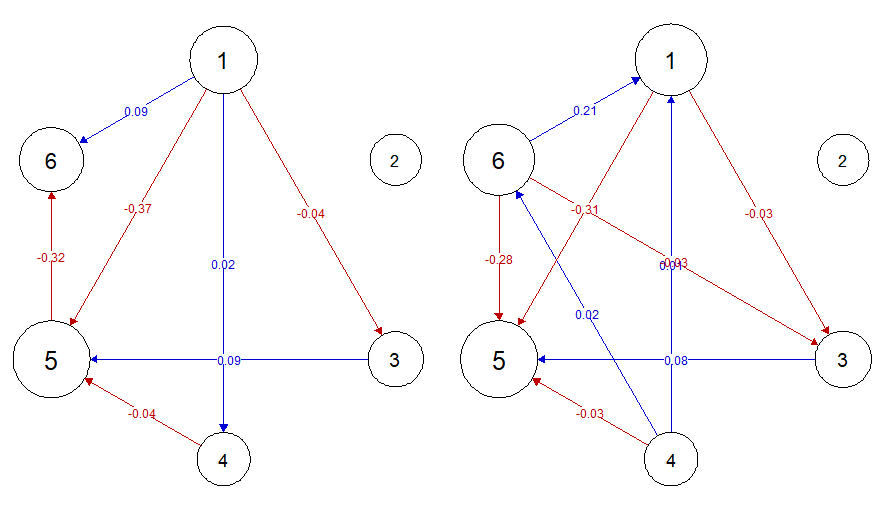
We also supply additional functions to aid in exploring the SE-set.

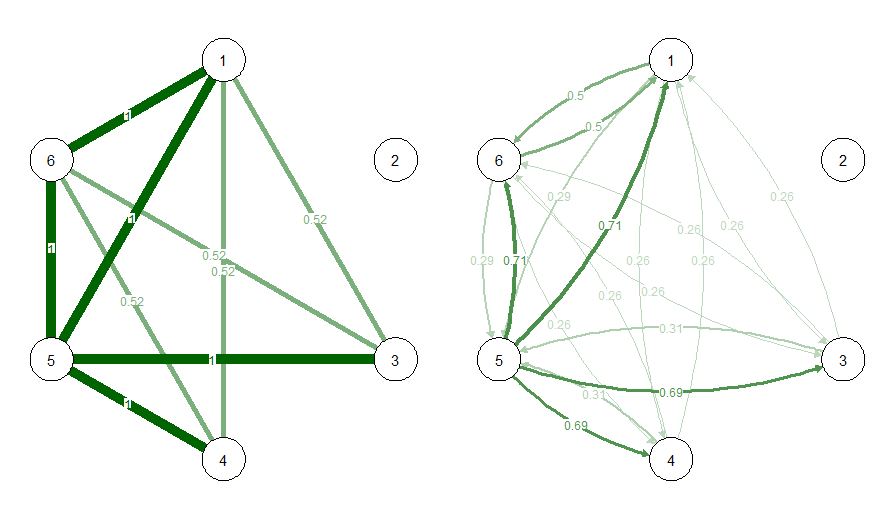
For example, the function propcal calculates the proportion of DAGs in the SE-set in which an edge between two variables is present. You can choose distinguish between the presence of some edge or an edge of a particular direction using the directed option

# Undirected edge frequency 
propu <- propcal(SE_example, rm_duplicate = F, directed = FALSE)

# Directed edge frequency
propd <- propcal(SE_example, rm_duplicate = F, directed = TRUE)

# Plot each as a network
par(mfrow=c(1,2))
qgraph(propu, edge.color = "darkgreen", layout = pnet$layout, edge.labels = T, maximum = 1)
qgraph(propd, edge.color = "darkgreen", layout = pnet$layout, edge.labels = T, maximum = 1)

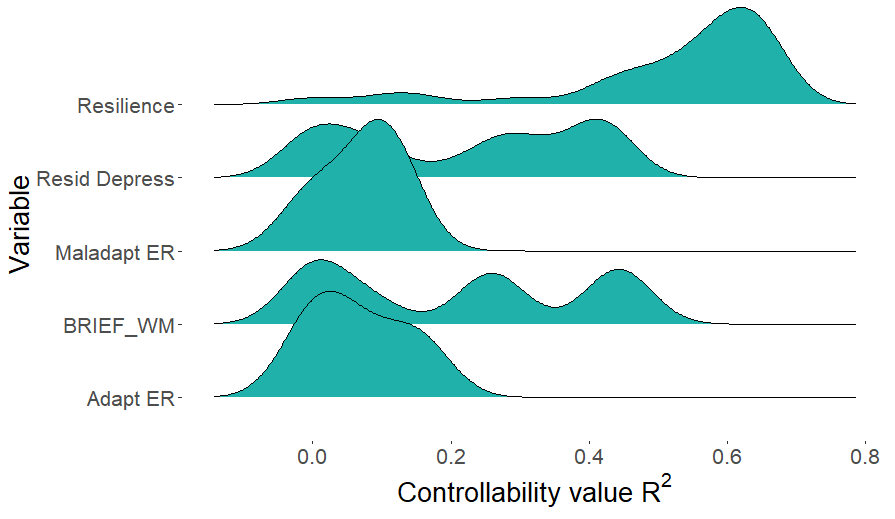
Given the SEset, you can essentially explore how any property of one graphical model varies across members. For example, we may be interested in the distribution of variance explained ($R^2$) for each variable when predicted by it's directed causes. This will differ across SEset members because the direct casues of any given variable will typically differ across the different path models. This can be computed using the r2_distribution function.

r2set <- r2_distribution(SEmatrix = SE_example, cormat = riskcor, names = NULL,
                         indices = c(1,3,4,5,6))

This distribution can be visualized, for instance using ggplot

library(tidyr)
library(ggplot2)
require(ggridges)
df <- as.data.frame(r2set, col.names = paste0("X",1:6))

df2 <- tidyr::gather(df)

p <- ggplot(df2, aes(y = key, x = value)) + 
  geom_density_ridges(fill = "light seagreen") + 
  labs(y = "Variable", x = expression(paste("Controllability value ", R^2)))
p + theme(text = element_text(size = 20), 
            axis.title.x = element_text(size = 20),
            axis.title.y = element_text(size = 20), 
            panel.background = element_blank())

Partial Correlations and Other Input Types

Alternatively, we can supply a matrix of partial correlations, such as output by the parcor package, or a (model-implied) covariance matrix using the input_type argument, demonstrated below.

# Using the partial correlation matrix as input
SE_example_2 <- network_to_SEset(parcor, digits = 2, rm_duplicates = TRUE, input_type = "parcor")
# Calculating the model-implied covariance matrix from the precision matrix
MIcov <- solve(omega)
SE_example_3 <- network_to_SEset(MIcov, digits = 2, rm_duplicates = TRUE, input_type = "MIcov")

Note only that, since the partial correlation matrix does not contain information on the diagonal elements of the precision matrix (that is, the partial variances), if a partial correlation matrix is supplied, we transform this to a correlation matrix using the corpcor package. As such, small numerical differences (approximately in the 7th decimal place) may be present depending on the input used.

Contact Details

For more details please contact [email protected].