Visualizing Collinearity Diagnostics.

VisCollin

Visualizing Collinearity Diagnostics

Version 0.1.2

The VisCollin package provides methods to calculate diagnostics for multicollinearity among predictors in a linear or generalized linear model. It also provides methods to visualize those diagnostics following Friendly & Kwan (2009), “Where’s Waldo: Visualizing Collinearity Diagnostics”, The American Statistician, 63, 56–65.

These include:

• better tabular presentation of collinearity diagnostics that highlight the important numbers.
• a semi-graphic tableplot of the diagnostics to make warning and danger levels more salient and
• a collinearity biplot of the smallest dimensions of predictor space, where collinearity is most apparent.

Installation

Tutorial example

library(VisCollin)
library(dplyr)
library(tidyr)
library(car)
library(corrplot)

This example uses the cars data set containing various measures of size and performance on 406 models of automobiles from 1982. Interest is focused on predicting gas mileage, mpg.

data(cars)
str(cars)
#> 'data.frame':    406 obs. of  10 variables:
#>  $ make    : Factor w/ 30 levels "amc","audi","bmw",..: 6 4 22 1 12 12 6 22 23 1 ...
#>  $ model   : chr  "chevelle" "skylark" "satellite" "rebel" ...
#>  $ mpg     : num  18 15 18 16 17 15 14 14 14 15 ...
#>  $ cylinder: int  8 8 8 8 8 8 8 8 8 8 ...
#>  $ engine  : num  307 350 318 304 302 429 454 440 455 390 ...
#>  $ horse   : int  130 165 150 150 140 198 220 215 225 190 ...
#>  $ weight  : int  3504 3693 3436 3433 3449 4341 4354 4312 4425 3850 ...
#>  $ accel   : num  12 11.5 11 12 10.5 10 9 8.5 10 8.5 ...
#>  $ year    : int  70 70 70 70 70 70 70 70 70 70 ...
#>  $ origin  : Factor w/ 3 levels "Amer","Eur","Japan": 1 1 1 1 1 1 1 1 1 1 ...

Fit a model

Fit a model predicting gas mileage (mpg) from the number of cylinders, engine displacement, horsepower, weight, time to accelerate from 0 – 60 mph and model year (1970–1982). Perhaps surprisingly, only weight and year appear to significantly predict gas mileage. What’s going on here?

cars.mod <- lm (mpg ~ cylinder + engine + horse + weight + accel + year, 
                data=cars)
Anova(cars.mod)
#> Anova Table (Type II tests)
#> 
#> Response: mpg
#>           Sum Sq  Df F value Pr(>F)    
#> cylinder      12   1    0.99   0.32    
#> engine        13   1    1.09   0.30    
#> horse          0   1    0.00   0.98    
#> weight      1214   1  102.84 <2e-16 ***
#> accel          8   1    0.70   0.40    
#> year        2419   1  204.99 <2e-16 ***
#> Residuals   4543 385                   
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

lmtest::coeftest() shows the coefficients, $\hat{\beta_j}$, their standard errors $s(\hat{\beta_j})$ and associated $t$ statistics, $t = \hat{\beta_j} / s(\hat{\beta_j})$. As we will see, the standard errors of the non-significant predictors have been inflated due to high multiple correlations among the predictors, making the $t$ statistics smaller.

lmtest::coeftest(cars.mod)
#> 
#> t test of coefficients:
#> 
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -1.45e+01   4.76e+00   -3.05   0.0024 ** 
#> cylinder    -3.30e-01   3.32e-01   -0.99   0.3212    
#> engine       7.68e-03   7.36e-03    1.04   0.2973    
#> horse       -3.91e-04   1.38e-02   -0.03   0.9775    
#> weight      -6.79e-03   6.70e-04  -10.14   <2e-16 ***
#> accel        8.53e-02   1.02e-01    0.84   0.4038    
#> year         7.53e-01   5.26e-02   14.32   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation matrix

It is often recommended to examine the correlation matrix of the predictors to diagnose collinearity problems. In the general case, this advice is misguided, because it is not the 0-order correlations that matter, but rather the multiple correlations predicting each independent variable from the others, $R_{x_j | \text{others}}$.

Nonetheless, it is instructive to examine the correlations.

R <- cars |> 
  select(cylinder:year) |> 
  tidyr::drop_na() |>
  cor()

100 * R |> round(digits = 2)
#>          cylinder engine horse weight accel year
#> cylinder      100     95    84     90   -52  -36
#> engine         95    100    90     93   -56  -38
#> horse          84     90   100     87   -70  -42
#> weight         90     93    87    100   -43  -32
#> accel         -52    -56   -70    -43   100   30
#> year          -36    -38   -42    -32    30  100

Or, better yet, use corrplot::corrplot.mixed() to visualize them, using color and shading of glyphs,

corrplot.mixed(R, lower = "square", upper = "ellipse", tl.col = "black")

The message here seems to be that there are two clusters of predictors with high correlations: {cylinder, engine, horse and weight}, and {accel, year}.

Variance inflation factors

Variance inflation factors measure the effect of multicollinearity on the standard errors of the estimated coefficients and are proportional to $1 / (1 - R^2_{x_j | \text{others}})$.

We check the variance inflation factors, using car::vif(). We see that most predictors have very high VIFs, indicating moderately severe multicollinearity.

vif(cars.mod)
#> cylinder   engine    horse   weight    accel     year 
#>    10.63    19.64     9.40    10.73     2.63     1.24

sqrt(vif(cars.mod))
#> cylinder   engine    horse   weight    accel     year 
#>     3.26     4.43     3.07     3.28     1.62     1.12

According to $\sqrt{\text{VIF}}$, the standard error of cylinder has been multiplied by 3.26 and it’s $t$-value divided by this number, compared with the case when all predictors are uncorrelated. engine, horse and weight suffer a similar fate.

Collinearity diagnostics

The diagnostic measures introduced by Belsley (1991) are based on the eigenvalues $\lambda_1, \lambda_2, \dots \lambda_p$ of the correlation matrix $R_{X}$ of the predictors (preferably centered and scaled, and not including the constant term for the intercept), and the corresponding eigenvectors in the columns of $\mathbf{V}_{p \times p}$.

colldiag() calculates:

• Condition indices: The smallest of the eigenvalues, those for which $\lambda_j \approx 0$, indicate collinearity and the number of small values indicates the number of near collinear relations. Because the sum of the eigenvalues, $\Sigma \lambda_i = p$ increases with the number of predictors $p$, it is useful to scale them all in relation to the largest. This leads to condition indices, defined as $\kappa_j = \sqrt{ \lambda_1 / \lambda_j}$. These have the property that the resulting numbers have common interpretations regardless of the number of predictors.

  • For completely uncorrelated predictors, all $\kappa_j = 1$.

  • $\kappa_j \rightarrow \infty$ as any $\lambda_k \rightarrow 0$.

  • In terms of the eigen-decomposition, variance inflation factors can be expressed as $$ \text{VIF}j = \sum{k=1}^{p} \frac{V^2_{jk}}{\lambda_k} ; . $$

• Variance decomposition proportions: Large VIFs indicate variables that are involved in some nearly collinear relations, but they don’t indicate which other variable(s) each is involved with. For this purpose, Belsley et. al. (1980) and Belsley (1991) proposed calculation of the proportions of variance of each variable associated with each principal component as a decomposition of the coefficient variance for each dimension.

For the current model, the usual display contains both the condition indices and variance proportions. However, even for a small example, it is often difficult to know what numbers to pay attention to.

(cd <- colldiag(cars.mod, center=TRUE))
#> Condition
#> Index    Variance Decomposition Proportions
#>           cylinder engine horse weight accel year 
#> 1   1.000 0.005    0.003  0.005 0.004  0.009 0.010
#> 2   2.252 0.004    0.002  0.000 0.007  0.022 0.787
#> 3   2.515 0.004    0.001  0.002 0.010  0.423 0.142
#> 4   5.660 0.309    0.014  0.306 0.087  0.063 0.005
#> 5   8.342 0.115    0.000  0.654 0.715  0.469 0.052
#> 6  10.818 0.563    0.981  0.032 0.176  0.013 0.004

Belsley (1991) recommends that the sources of collinearity be diagnosed (a) only for those components with large $\kappa_j$, and (b) for those components for which the variance proportion is large (say, $\ge 0.5$) on two or more predictors. The print method for "colldiag" objects has a fuzz argument controlling this.

print(cd, fuzz = 0.5)
#> Condition
#> Index    Variance Decomposition Proportions
#>           cylinder engine horse weight accel year 
#> 1   1.000  .        .      .     .      .     .   
#> 2   2.252  .        .      .     .      .    0.787
#> 3   2.515  .        .      .     .      .     .   
#> 4   5.660  .        .      .     .      .     .   
#> 5   8.342  .        .     0.654 0.715   .     .   
#> 6  10.818 0.563    0.981   .     .      .     .

The mystery is solved: There are two nearly collinear relations among the predictors, corresponding to the two smallest dimensions.

• Dimension 5 reflects the high correlation between horsepower and weight,
• Dimension 6 reflects the high correlation between number of cylinders and engine displacement.

Note that the high variance proportion for year (0.787) on the second component creates no problem and should be ignored because (a) the condition index is low and (b) it shares nothing with other predictors.

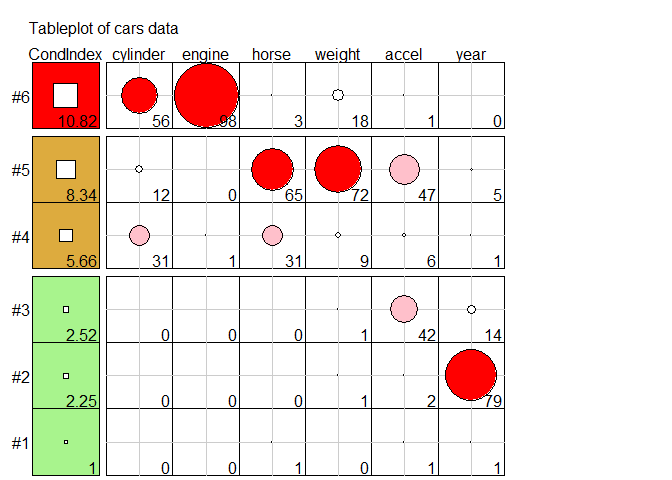
Tableplot

The simplified tabular display above can be improved to make the patterns of collinearity more visually apparent and to signify warnings directly to the eyes. A “tableplot” (Kwan et-al., 2009) is a semi-graphic display that presents numerical information in a table using shapes proportional to the value in a cell and other visual attributes (shape type, color fill, and so forth) to encode other information.

For collinearity diagnostics, these show:

• the condition indices, using using squares whose background color is red for condition indices > 10, green for values > 5 and green otherwise, reflecting danger, warning and OK respectively. The value of the condition index is encoded within this using a white square whose side is proportional to the value (up to some maximum value, cond.max).
• Variance decomposition proportions are shown by filled circles whose radius is proportional to those values and are filled (by default) with shades ranging from white through pink to red. Rounded values of those diagnostics are printed in the cells.

The tableplot below encodes all the information from the values of colldiag() printed above (but using prop.col color breaks such that variance proportions < 0.3 are shaded white). The visual message is that one should attend to collinearities with large condition indices and large variance proportions implicating two or more predictors.

tableplot(cd, title = "Tableplot of cars data", cond.max = 30 )

Collinearity biplot

The standard biplot (Gabriel, 1971; Gower& Hand 1996) can be regarded as a multivariate analog of a scatterplot, obtained by projecting a multivariate sample into a low-dimensional space (typically of 2 or 3 dimensions) accounting for the greatest variance in the data. With the symmetric (PCA) scaling used here, this is equivalent to a plot of principal component scores of the mean-centered matrix $\widetilde{\mathbf{X}} = \mathbf{X} - \bar{\mathbf{X}}$ of predictors for the observations (shown as points or case labels), together with principal component coefficients for the variables (shown as vectors) in the same 2D (or 3D) space.

However the standard biplot is less useful for visualizing the relations among the predictors that lead to nearly collinear relations. Instead, biplots of the smallest dimensions show these relations directly, and can show other features of the data as well, such as outliers and leverage points. We use prcomp(X, scale.=TRUE) to obtain the PCA of the correlation matrix of the predictors:

cars.X <- cars |>
  select(where(is.numeric)) |>
  select(-mpg) |>
  tidyr::drop_na()
cars.pca <- prcomp(cars.X, scale. = TRUE)
cars.pca
#> Standard deviations (1, .., p=6):
#> [1] 2.070 0.911 0.809 0.367 0.245 0.189
#> 
#> Rotation (n x k) = (6 x 6):
#>             PC1    PC2    PC3    PC4     PC5     PC6
#> cylinder -0.454 0.1869 -0.168  0.659 -0.2711  0.4725
#> engine   -0.467 0.1628 -0.134  0.193 -0.0109 -0.8364
#> horse    -0.462 0.0177  0.123 -0.620 -0.6123  0.1067
#> weight   -0.444 0.2598 -0.278 -0.350  0.6860  0.2539
#> accel     0.330 0.2098 -0.865 -0.143 -0.2774 -0.0337
#> year      0.237 0.9092  0.335 -0.025 -0.0624 -0.0142

The standard deviations above are the square roots $\sqrt{\lambda_j}$ of the eigenvalues of the correlation matrix, and are returned in the sdev component of the "prcomp" object. The eigenvectors are returned in the rotation component, whose directions are arbitrary.

# Make labels for dimensions include % of variance
pct <- 100 *(cars.pca$sdev^2) / sum(cars.pca$sdev^2)
lab <- glue::glue("Dimension {1:6} ({round(pct, 2)}%)")

# Direction of eigenvectors is arbitrary. Reflect them
cars.pca$rotation <- -cars.pca$rotation

The collinearity biplot is then constructed as follows:

op <- par(lwd = 2, xpd = NA )
biplot(cars.pca,
       choices=6:5,           # only the last two dimensions
       scale=0.5,             # symmetric biplot scaling
       cex=c(0.6, 1),         # character sizes for points and vectors
       col = c("black", "blue"),
       expand = 1.7,          # expand variable vectors for visibility
       xlab = lab[6],
       ylab = lab[5],
       xlim = c(-0.7, 0.5),
       ylim = c(-0.8, 0.5)
      )
par(op)

The projections of the variable vectors on the Dimension 5 and Dimension 6 axes are proportional to their variance proportions shown above. The relative lengths of these variable vectors can be considered to indicate the extent to which each variable contributes to collinearity for these two near-singular dimensions.

Thus, we see again that Dimension 6 is largely determined by engine size, with a substantial (negative) relation to cylinder. Dimension 5 has its’ strongest relations to weight and horse.

Moreover, there is one observation, #20, that stands out as an outlier in predictor space, far from the centroid. It turns out that this vehicle, a Buick Estate wagon, is an early-year (1970) American behemoth, with an 8-cylinder, 455 cu. in, 225 horse-power engine, and able to go from 0 to 60 mph in 10 sec. (Its MPG is only slightly under-predicted from the regression model, however.)

Remedies for collinearity: What to do?

Collinearity is often a data problem, for which there is no magic cure. Nevertheless there are some general guidelines and useful techniques to address this problem.

• Pure prediction: If we are only interested in predicting / explaining an outcome, and not the model coefficients or which are “significant”, collinearity can be largely ignored. The fitted values are unaffected by collinearity.

• structural collinearity: Sometimes collinearity results from structural relations among the variables:

  • For example, polynomial terms, like $x, x^2, x^3$ or interaction terms like $x_1, x_2, x_1 * x_2$ are necessarily correlated. A simple cure is to center the predictors at their means, using $x - \bar{x}, (x - \bar{x})^2, (x - \bar{x})^3$ or $(x_1 - \bar{x}_1), (x_2 - \bar{x}_2), (x_1 - \bar{x}_1) * (x_2 - \bar{x}_2)$

  • When some predictors share a common cause, as in GNP or population in time-series or cross-national data, you can reduce collinearity by re-defining predictors to reflect per capita measures.

• Model re-specification:

  • Drop one or more regressors that have a high VIF if they are not deemed to be essential

  • Replace highly correlated regressors with linear combination(s) of them. For example, two related variables, $x_1$ and $x_2$ can be replaced without any loss of information by replacing them with their sum and difference, $z_1 = x_1 + x_2$ and $z_2 = x_1 - x_2$.

• Statistical remedies:

  • Transform the predictors to uncorrelated principal components

  • use regularization methods such as ridge regression and lasso, which correct for collinearity by introducing shrinking coefficients towards 0, introducing a small amount of bias, . See the genridge package and its pkgdown documentation for visualization methods.

  • use Bayesian regression; if multicollinearity prevents a regression coefficient from being estimated precisely, then a prior on that coefficient will help to reduce its posterior variance.

References

Belsley, D.A., Kuh, E. and Welsch, R. (1980). Regression Diagnostics, New York: John Wiley & Sons.

Belsley, D.A. (1991). Conditioning diagnostics, collinearity and weak data in regression. New York: John Wiley & Sons.

Friendly, M., & Kwan, E. (2009). “Where’s Waldo: Visualizing Collinearity Diagnostics.” The American Statistician, 63, 56–65. Online: https://www.datavis.ca/papers/viscollin-tast.pdf. Supp. materials: https://www.datavis.ca/papers/viscollin/

Gabriel, K. R. (1971). The Biplot Graphic Display of Matrices with Application to Principal Components Analysis. Biometrics, 58, 453–467.

Gower, J. C., & Hand, D. J. (1996). Biplots. London: Chapman & Hall.

Kwan, E., Lu, I. R. R., & Friendly, M. (2009). Tableplot: A new tool for assessing precise predictions. Zeitschrift Für Psychologie / Journal of Psychology, 217, 38–48.