Behavioral Economic Easy Demand.
Behavioral Economic (be) Easy (ez) Demand
Behavioral economic demand is gaining in popularity. The motivation behind beezdemand was to create an alternative tool to conduct these analyses. This package is not necessarily meant to be a replacement for other softwares; rather, it is meant to serve as an additional tool in the behavioral economist’s toolbox. It is meant for researchers to conduct behavioral economic (be) demand the easy (ez) way.
Note About Use
Currently, this version (0.1.0) is the first minor release and is stable. I encourage you to use it but be aware that, as with any software release, there might be (unknown) bugs present. I’ve tried hard to make this version usable while including the core functionality (described more below). However, if you find issues or would like to contribute, please open an issue on my GitHub page or email me.
Installing beezdemand
CRAN Release (recommended method)
The latest stable version of beezdemand (currently v.0.1.0) can be found on CRAN and installed using the following command. The first time you install the package, you may be asked to select a CRAN mirror. Simply select the mirror geographically closest to you.
install.packages("beezdemand")
library(beezdemand)
GitHub Release
To install a stable release directly from GitHub, first install and load the devtools package. Then, use install_github to install the package and associated vignette. You don’t need to download anything directly from GitHub, as you should use the following instructions:
install.packages("devtools")
devtools::install_github("brentkaplan/beezdemand", build_vignettes = TRUE)
library(beezdemand)
GitHub Development Version
To install the development version of the package, specify the development branch in install_github:
devtools::install_github("brentkaplan/beezdemand@develop")
Using the Package
Example Dataset
An example dataset of responses on an Alcohol Purchase Task is provided. This object is called apt and is located within the beezdemand package. These data are a subset of from the paper by Kaplan & Reed (2018). Participants (id) reported the number of alcoholic drinks (y) they would be willing to purchase and consume at various prices (x; USD). Note the format of the data, which is called “long format”. Long format data are data structured such that repeated observations are stacked in multiple rows, rather than across columns. First, take a look at an extract of the dataset apt, where I’ve subsetted rows 1 through 10 and 17 through 26:
| id | x | y | |
|---|---|---|---|
| 1 | 19 | 0.0 | 10 |
| 2 | 19 | 0.5 | 10 |
| 3 | 19 | 1.0 | 10 |
| 4 | 19 | 1.5 | 8 |
| 5 | 19 | 2.0 | 8 |
| 6 | 19 | 2.5 | 8 |
| 7 | 19 | 3.0 | 7 |
| 8 | 19 | 4.0 | 7 |
| 9 | 19 | 5.0 | 7 |
| 10 | 19 | 6.0 | 6 |
| 17 | 30 | 0.0 | 3 |
| 18 | 30 | 0.5 | 3 |
| 19 | 30 | 1.0 | 3 |
| 20 | 30 | 1.5 | 3 |
| 21 | 30 | 2.0 | 2 |
| 22 | 30 | 2.5 | 2 |
| 23 | 30 | 3.0 | 2 |
| 24 | 30 | 4.0 | 2 |
| 25 | 30 | 5.0 | 2 |
| 26 | 30 | 6.0 | 2 |
The first column contains the row number. The second column contains the id number of the series within the dataset. The third column contains the x values (in this specific dataset, price per drink) and the fourth column contains the associated responses (number of alcoholic drinks purchased at each respective price). There are replicates of id because for each series (or participant), several x values were presented.
Converting from Wide to Long and Vice Versa
Take for example the format of most datasets that would be exported from a data collection software such as Qualtrics or SurveyMonkey or Google Forms:
## the following code takes the apt data, which are in long format, and converts
## to a wide format that might be seen from data collection software
wide <- spread(apt, x, y)
colnames(wide) <- c("id", paste0("price_", seq(1, 16, by = 1)))
knitr::kable(wide[1:5, 1:10])
| id | price_1 | price_2 | price_3 | price_4 | price_5 | price_6 | price_7 | price_8 | price_9 |
|---|---|---|---|---|---|---|---|---|---|
| 19 | 10 | 10 | 10 | 8 | 8 | 8 | 7 | 7 | 7 |
| 30 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 |
| 38 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 |
| 60 | 10 | 10 | 8 | 8 | 6 | 6 | 5 | 5 | 4 |
| 68 | 10 | 10 | 9 | 9 | 8 | 8 | 7 | 6 | 5 |
A dataset such as this is referred to as “wide format” because each participant series contains a single row and multiple measurements within the participant are indicated by the columns. This data format is fine for some purposes; however, for beezdemand, data are required to be in “long format” (in the same format as the example data described earlier). In order to convert to the long format, some steps will be required.
First, it is helpful to rename the columns to what the prices actually were. For example, for the purposes of our example dataset, price_1 was $0.00 (free), price_2 was $0.50, price_3 was $1.00, and so on.
## make an object to hold what will be the new column names
newcolnames <- c("id", "0", "0.5", "1", "1.50", "2", "2.50", "3",
"4", "5", "6", "7", "8", "9", "10", "15", "20")
## current column names
colnames(wide)
[1] "id" "price_1" "price_2" "price_3" "price_4" "price_5"
[7] "price_6" "price_7" "price_8" "price_9" "price_10" "price_11"
[13] "price_12" "price_13" "price_14" "price_15" "price_16"
## replace current column names with new column names
colnames(wide) <- newcolnames
## how new data look (first 5 rows only)
knitr::kable(wide[1:5, ])
| id | 0 | 0.5 | 1 | 1.50 | 2 | 2.50 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 19 | 10 | 10 | 10 | 8 | 8 | 8 | 7 | 7 | 7 | 6 | 6 | 5 | 5 | 4 | 3 | 2 |
| 30 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 |
| 38 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 0 | 0 |
| 60 | 10 | 10 | 8 | 8 | 6 | 6 | 5 | 5 | 4 | 4 | 3 | 3 | 2 | 2 | 0 | 0 |
| 68 | 10 | 10 | 9 | 9 | 8 | 8 | 7 | 6 | 5 | 5 | 5 | 4 | 4 | 3 | 0 | 0 |
Now we can convert into a long format using some of the helpful functions in the tidyverse package (make sure the package is loaded before trying the commands below).
## using the dataframe 'wide', we specify the key will be 'price', the values
## will be 'consumption', and we will select all columns besides the first ('id')
long <- tidyr::gather(wide, price, consumption, -id)
## we'll sort the rows by id
long <- arrange(long, id)
## view the first 20 rows
knitr::kable(long[1:20, ])
| id | price | consumption |
|---|---|---|
| 19 | 0 | 10 |
| 19 | 0.5 | 10 |
| 19 | 1 | 10 |
| 19 | 1.50 | 8 |
| 19 | 2 | 8 |
| 19 | 2.50 | 8 |
| 19 | 3 | 7 |
| 19 | 4 | 7 |
| 19 | 5 | 7 |
| 19 | 6 | 6 |
| 19 | 7 | 6 |
| 19 | 8 | 5 |
| 19 | 9 | 5 |
| 19 | 10 | 4 |
| 19 | 15 | 3 |
| 19 | 20 | 2 |
| 30 | 0 | 3 |
| 30 | 0.5 | 3 |
| 30 | 1 | 3 |
| 30 | 1.50 | 3 |
Two final modifications we will make will be to (1) rename our columns to what the functions in beezdemand will expect to see: id, x, and y, and (2) ensure both x and y are in numeric format.
colnames(long) <- c("id", "x", "y")
long$x <- as.numeric(long$x)
long$y <- as.numeric(long$y)
knitr::kable(head(long))
| id | x | y |
|---|---|---|
| 19 | 0.0 | 10 |
| 19 | 0.5 | 10 |
| 19 | 1.0 | 10 |
| 19 | 1.5 | 8 |
| 19 | 2.0 | 8 |
| 19 | 2.5 | 8 |
The dataset is now “tidy” because: (1) each variable forms a column, (2) each observation forms a row, and (3) each type of observational unit forms a table (in this case, our observational unit is the Alcohol Purchase Task data). To learn more about the benefits of tidy data, readers are encouraged to consult Hadley Wikham’s essay on Tidy Data.
Obtain Descriptive Data
Descriptive values of responses at each price can be obtained easily. The resulting table includes mean, standard deviation, proportion of zeros, number of NAs, and minimum and maximum values. If bwplot = TRUE, a box-and-whisker plot is also created and saved. By default, this location is a folder named “plots” one level up from the current working directory. The user may additionally specify the directory that the plot should save into, the type of file (either "png" or "pdf"), and the filename. Notice the red crosses indicate the mean. Defaults are shown here:
GetDescriptives(dat = apt, bwplot = FALSE, outdir = "../plots/", device = "png",
filename = "bwplot")
To actually run the code and generate the file, we will turn bwplot = TRUE. The function will create a folder one level higher than the current folder (i.e., the ../ portion) and save the file, “bwplot.png” in the folder.
GetDescriptives(dat = apt, bwplot = TRUE, outdir = plotdir, device = "png",
filename = "bwplot")
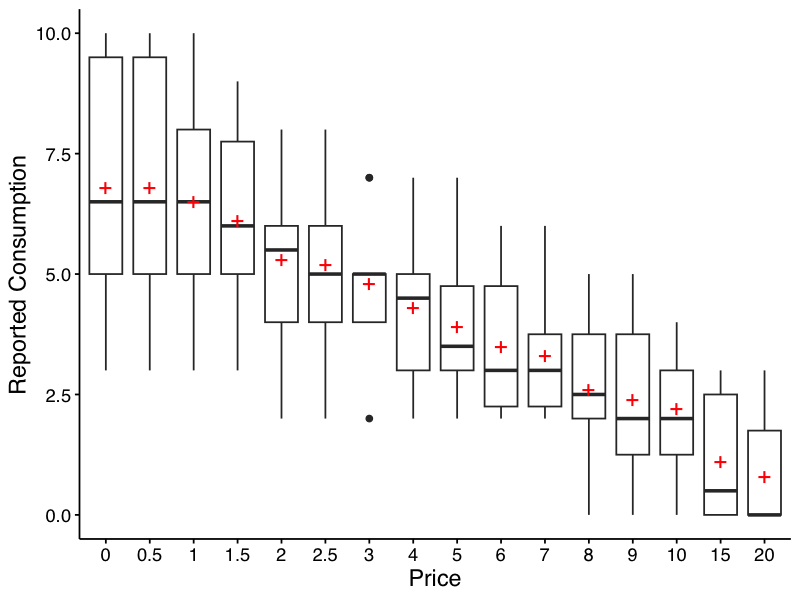
And here is the table that is returned from the function:
| Price | Mean | Median | SD | PropZeros | NAs | Min | Max |
|---|---|---|---|---|---|---|---|
| 0 | 6.8 | 6.5 | 2.62 | 0.0 | 0 | 3 | 10 |
| 0.5 | 6.8 | 6.5 | 2.62 | 0.0 | 0 | 3 | 10 |
| 1 | 6.5 | 6.5 | 2.27 | 0.0 | 0 | 3 | 10 |
| 1.5 | 6.1 | 6.0 | 1.91 | 0.0 | 0 | 3 | 9 |
| 2 | 5.3 | 5.5 | 1.89 | 0.0 | 0 | 2 | 8 |
| 2.5 | 5.2 | 5.0 | 1.87 | 0.0 | 0 | 2 | 8 |
| 3 | 4.8 | 5.0 | 1.48 | 0.0 | 0 | 2 | 7 |
| 4 | 4.3 | 4.5 | 1.57 | 0.0 | 0 | 2 | 7 |
| 5 | 3.9 | 3.5 | 1.45 | 0.0 | 0 | 2 | 7 |
| 6 | 3.5 | 3.0 | 1.43 | 0.0 | 0 | 2 | 6 |
| 7 | 3.3 | 3.0 | 1.34 | 0.0 | 0 | 2 | 6 |
| 8 | 2.6 | 2.5 | 1.51 | 0.1 | 0 | 0 | 5 |
| 9 | 2.4 | 2.0 | 1.58 | 0.1 | 0 | 0 | 5 |
| 10 | 2.2 | 2.0 | 1.32 | 0.1 | 0 | 0 | 4 |
| 15 | 1.1 | 0.5 | 1.37 | 0.5 | 0 | 0 | 3 |
| 20 | 0.8 | 0.0 | 1.14 | 0.6 | 0 | 0 | 3 |
Change Data
There are certain instances in which data are to be modified before fitting, for example when using an equation that logarithmically transforms y values. The following function can help with modifying data:
nreplindicates number of replacement 0 values, either as an integer or"all". If this value is an integer,n, then the firstn0s will be replaced.replnumindicates the number that should replace 0 valuesrem0removes all zerosremq0eremoves y value where x (or price) equals 0replfreereplaces where x (or price) equals 0 with a specified number
ChangeData(dat = apt, nrepl = 1, replnum = 0.01, rem0 = FALSE, remq0e = FALSE,
replfree = NULL)
Identify Unsystematic Responses
Using the following function, we can examine the consistency of demand data using Stein et al.’s (2015) alogrithm for identifying unsystematic responses. Default values shown, but they can be customized.
CheckUnsystematic(dat = apt, deltaq = 0.025, bounce = 0.1, reversals = 0, ncons0 = 2)
| id | TotalPass | DeltaQ | DeltaQPass | Bounce | BouncePass | Reversals | ReversalsPass | NumPosValues |
|---|---|---|---|---|---|---|---|---|
| 19 | 3 | 0.2112 | Pass | 0 | Pass | 0 | Pass | 16 |
| 30 | 3 | 0.1437 | Pass | 0 | Pass | 0 | Pass | 16 |
| 38 | 3 | 0.7885 | Pass | 0 | Pass | 0 | Pass | 14 |
| 60 | 3 | 0.9089 | Pass | 0 | Pass | 0 | Pass | 14 |
| 68 | 3 | 0.9089 | Pass | 0 | Pass | 0 | Pass | 14 |
Analyze Demand Data
Results of the analysis return both empirical and derived measures for use in additional analyses and model specification. Equations include the linear model, exponential model, and exponentiated model. Soon, I will be including the nonlinear mixed effects model, mixed effects versions of the exponential and exponentiated model, and others. However, currently these models are not yet supported.
Obtaining Empirical Measures
Empirical measures can be obtained separately on their own:
GetEmpirical(dat = apt)
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| 19 | 10 | NA | 20 | 45 | 15 |
| 30 | 3 | NA | 20 | 20 | 20 |
| 38 | 4 | 15 | 10 | 21 | 7 |
| 60 | 10 | 15 | 10 | 24 | 8 |
| 68 | 10 | 15 | 10 | 36 | 9 |
Obtaining Derived Measures
FitCurves() has several important arguments that can be passed. For the purposes of this document, focus will be on the two contemporary demand equations.
equation = "hs"is the default but can accept the character strings"linear","hs", or"koff", the latter two of which are the contemporary equations proposed by Hursh & Silberberg (2008) and Koffarnus et al. (2015), respectively.kcan take accept a specific number but by default will be calculated based on the maximum and minimum y values of the entire sample and adding .5. Adding this amount was originally proposed by Steven R. Hursh in an early iteration of a Microsoft Excel spreadsheet used to calculate demand metrics. This adjustment was adopted for two reasons. First, when fitting $Q_0$ as a derived parameter, the value may exceed the empirically observed intensity value. Thus, a k value calculated based only on the observed range of data may underestimate the full fitted range of the curve. Second, we have found that values of $\alpha$ (as well as values that rely on $\alpha$, i.e. approximate $P_{max}$) display greater discrepancies when smaller values of k are used compared to larger values of k. Other options include"ind", which will calculate k based on individual basis,"fit", which will fit k as a free parameter on an individual basis,"share", which will fit k as a single shared parameter across all data sets (while fitting individual $Q_0$ and $\alpha$).agg = NULLis the default, which means no aggregation. Whenagg = "Mean", models are fit to the averaged data disregarding any error. Whenagg = "Pooled", all data are used and clustering within individual is ignored.detailed = FALSEis the default. This will output a single dataframe of results, as shown below. Whendetailed = TRUE, the output is a 3 element list that includes (1) dataframe of results, (2) list of nonlinear regression model objects, (3) list of dataframes containing predicted x and y values (to be used in subsequent plotting), and (4) list of individual dataframes used in fitting.loboundandhiboundcan accept named vectors that will be used as lower and upper bounds, respectively during fitting. Ifk = "fit", then it should look as follows (values are nonspecific):lobound = c("q0" = 0, "k" = 0, "alpha" = 0)andhibound = c("q0" = 25, "k" = 10, "alpha" = 1). Ifkis not being fit as a parameter, then only"q0"and"alpha"should be used in bounding.
Note: Fitting with an equation (e.g., "linear", "hs") that doesn’t work happily with zero consumption values results in the following. One, a message will appear saying that zeros are incompatible with the equation. Two, because zeros are removed prior to finding empirical (i.e., observed) measures, resulting BP0 values will be all NAs (reflective of the data transformations). The warning message will look as follows:
Warning message:
Zeros found in data not compatible with equation! Dropping zeros!
The simplest use of FitCurves() is shown here, only needing to specify dat and equation. All other arguments shown are set to their default values.
FitCurves(dat = apt, equation = "hs", agg = NULL, detailed = FALSE,
xcol = "x", ycol = "y", idcol = "id", groupcol = NULL)
Which is equivalent to:
FitCurves(dat = apt, equation = "hs")
Note that this ouput returns a message (No k value specified. Defaulting to empirical mean range +.5) and the aforementioned warning (Warning message: Zeros found in data not compatible with equation! Dropping zeros!). With detailed = FALSE, the only output is the dataframe of results (broken up to show the different types of results). This example fits the exponential equation proposed by Hursh & Silberberg (2008):
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| 19 | 10 | NA | 20 | 45 | 15 |
| 30 | 3 | NA | 20 | 20 | 20 |
| 38 | 4 | NA | 10 | 21 | 7 |
| 60 | 10 | NA | 10 | 24 | 8 |
| 68 | 10 | NA | 10 | 36 | 9 |
Empirical Measures
| Equation | Q0d | K | Alpha | R2 |
|---|---|---|---|---|
| hs | 10.475734 | 1.031479 | 0.0046571 | 0.9660008 |
| hs | 2.932406 | 1.031479 | 0.0134557 | 0.7922379 |
| hs | 4.523155 | 1.031479 | 0.0087935 | 0.8662632 |
| hs | 10.492133 | 1.031479 | 0.0102231 | 0.9664814 |
| hs | 10.651760 | 1.031479 | 0.0061262 | 0.9699408 |
Fitted Measures
| Q0se | Alphase | N | AbsSS | SdRes | Q0Low | Q0High | AlphaLow | AlphaHigh |
|---|---|---|---|---|---|---|---|---|
| 0.4159581 | 0.0002358 | 16 | 0.0193354 | 0.0371632 | 9.583593 | 11.367876 | 0.0041515 | 0.0051628 |
| 0.2506946 | 0.0017321 | 16 | 0.0978350 | 0.0835955 | 2.394720 | 3.470093 | 0.0097408 | 0.0171706 |
| 0.2357693 | 0.0008878 | 14 | 0.0259083 | 0.0464653 | 4.009458 | 5.036853 | 0.0068592 | 0.0107277 |
| 0.6219724 | 0.0005118 | 14 | 0.0236652 | 0.0444083 | 9.136972 | 11.847295 | 0.0091080 | 0.0113382 |
| 0.3841063 | 0.0002713 | 14 | 0.0109439 | 0.0301992 | 9.814865 | 11.488656 | 0.0055350 | 0.0067173 |
Uncertainty and Model Information
| EV | Omaxd | Pmaxd | Omaxa |
|---|---|---|---|
| 2.0496977 | 45.49394 | 14.393108 | 47.84770 |
| 0.7094191 | 15.74587 | 17.796228 | 16.56052 |
| 1.0855465 | 24.09418 | 17.654531 | 25.34076 |
| 0.9337419 | 20.72481 | 6.546547 | 21.79707 |
| 1.5581899 | 34.58471 | 10.760891 | 36.37405 |
Derived Measures
Here, the simplest form is shown specifying another equation, "koff". This fits the modified exponential equation proposed by Koffarnus et al. (2015):
FitCurves(dat = apt, equation = "koff")
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| 19 | 10 | NA | 20 | 45 | 15 |
| 30 | 3 | NA | 20 | 20 | 20 |
| 38 | 4 | 15 | 10 | 21 | 7 |
| 60 | 10 | 15 | 10 | 24 | 8 |
| 68 | 10 | 15 | 10 | 36 | 9 |
Empirical Measures
| Equation | Q0d | K | Alpha | R2 |
|---|---|---|---|---|
| koff | 10.131767 | 1.429419 | 0.0029319 | 0.9668576 |
| koff | 2.989613 | 1.429419 | 0.0093716 | 0.8136932 |
| koff | 4.607551 | 1.429419 | 0.0070562 | 0.8403625 |
| koff | 10.371088 | 1.429419 | 0.0068127 | 0.9659117 |
| koff | 10.703627 | 1.429419 | 0.0044361 | 0.9444897 |
Fitted Measures
| Q0se | Alphase | N | AbsSS | SdRes | Q0Low | Q0High | AlphaLow | AlphaHigh |
|---|---|---|---|---|---|---|---|---|
| 0.2438729 | 0.0001663 | 16 | 2.908243 | 0.4557758 | 9.608712 | 10.654822 | 0.0025752 | 0.0032886 |
| 0.1721284 | 0.0013100 | 16 | 1.490454 | 0.3262837 | 2.620434 | 3.358792 | 0.0065620 | 0.0121812 |
| 0.3078231 | 0.0010631 | 16 | 4.429941 | 0.5625161 | 3.947336 | 5.267766 | 0.0047761 | 0.0093362 |
| 0.4069382 | 0.0004577 | 16 | 5.010982 | 0.5982703 | 9.498292 | 11.243884 | 0.0058310 | 0.0077945 |
| 0.4677467 | 0.0003736 | 16 | 8.350830 | 0.7723263 | 9.700410 | 11.706844 | 0.0036349 | 0.0052373 |
Uncertainty and Model Information
| EV | Omaxd | Pmaxd | Omaxa |
|---|---|---|---|
| 1.9957818 | 46.56622 | 15.140905 | 46.70800 |
| 0.6243741 | 14.56810 | 16.052915 | 14.61245 |
| 0.8292621 | 19.34861 | 13.833934 | 19.40752 |
| 0.8588915 | 20.03993 | 6.365580 | 20.10095 |
| 1.3190323 | 30.77608 | 9.472147 | 30.86979 |
Derived Measures
By specifying agg = "Mean", y values at each x value are aggregated and a single curve is fit to the data (disregarding error around each averaged point):
FitCurves(dat = apt, equation = "hs", agg = "Mean")
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| mean | 6.8 | NA | 20 | 23.1 | 7 |
Empirical Measures
| Equation | Q0d | K | Alpha | R2 |
|---|---|---|---|---|
| hs | 7.637436 | 1.429419 | 0.0066817 | 0.9807508 |
Fitted Measures
| Q0se | Alphase | N | AbsSS | SdRes | Q0Low | Q0High | AlphaLow | AlphaHigh |
|---|---|---|---|---|---|---|---|---|
| 0.3258955 | 0.0002218 | 16 | 0.02187 | 0.039524 | 6.93846 | 8.336413 | 0.0062059 | 0.0071574 |
Uncertainty and Model Information
| EV | Omaxd | Pmaxd | Omaxa |
|---|---|---|---|
| 0.875742 | 20.43309 | 8.813584 | 20.49531 |
Derived Measures
By specifying agg = "Pooled", y values at each x value are aggregated and a single curve is fit to the data and error around each averaged point (but disregarding within-subject clustering):
FitCurves(dat = apt, equation = "hs", agg = "Pooled")
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| pooled | 6.8 | NA | 20 | 23.1 | 7 |
Empirical Measures
| Equation | Q0d | K | Alpha | R2 |
|---|---|---|---|---|
| hs | 6.592488 | 1.031479 | 0.0085032 | 0.460412 |
Fitted Measures
| Q0se | Alphase | N | AbsSS | SdRes | Q0Low | Q0High | AlphaLow | AlphaHigh |
|---|---|---|---|---|---|---|---|---|
| 0.4260507 | 0.0007125 | 146 | 4.677846 | 0.1802361 | 5.750367 | 7.434609 | 0.0070949 | 0.0099115 |
Uncertainty and Model Information
| EV | Omaxd | Pmaxd | Omaxa |
|---|---|---|---|
| 1.122607 | 24.91675 | 12.52644 | 26.20589 |
Derived Measures
Share k Globally; Fit Other Parameters Locally
As mentioned earlier, in the function FitCurves, when k = "share" this parameter will be a shared parameter across all datasets (globally) while estimating $Q_0$ and $\alpha$ locally. While this works, it may take some time with larger sample sizes.
FitCurves(dat = apt, equation = "hs", k = "share")
| id | Intensity | BP0 | BP1 | Omaxe | Pmaxe |
|---|---|---|---|---|---|
| 19 | 10 | NA | 20 | 45 | 15 |
| 30 | 3 | NA | 20 | 20 | 20 |
| 38 | 4 | NA | 10 | 21 | 7 |
| 60 | 10 | NA | 10 | 24 | 8 |
| 68 | 10 | NA | 10 | 36 | 9 |
Empirical Measures
| Equation | Q0d | K | Alpha | R2 |
|---|---|---|---|---|
| hs | 10.014576 | 3.31833 | 0.0011616 | 0.9820968 |
| hs | 2.766313 | 3.31833 | 0.0033331 | 0.7641766 |
| hs | 4.485810 | 3.31833 | 0.0024580 | 0.8803145 |
| hs | 9.721379 | 3.31833 | 0.0024219 | 0.9705985 |
| hs | 10.293139 | 3.31833 | 0.0015879 | 0.9722310 |
Fitted Measures
| Q0se | Alphase | N | AbsSS | SdRes | Q0Low | Q0High | AlphaLow | AlphaHigh |
|---|---|---|---|---|---|---|---|---|
| 0.2429150 | 0.0000308 | 16 | 0.0101816 | 0.0269677 | 9.493575 | 10.535577 | 0.0010955 | 0.0012277 |
| 0.2192797 | 0.0003739 | 16 | 0.1110490 | 0.0890622 | 2.296005 | 3.236621 | 0.0025312 | 0.0041350 |
| 0.2074990 | 0.0001963 | 14 | 0.0231862 | 0.0439566 | 4.033709 | 4.937912 | 0.0020302 | 0.0028858 |
| 0.4371060 | 0.0000778 | 14 | 0.0207584 | 0.0415916 | 8.769006 | 10.673751 | 0.0022523 | 0.0025914 |
| 0.3179671 | 0.0000523 | 14 | 0.0101100 | 0.0290259 | 9.600348 | 10.985930 | 0.0014740 | 0.0017018 |
Uncertainty and Model Information
| EV | Omaxd | Pmaxd | Omaxa |
|---|---|---|---|
| 1.4241862 | 44.55169 | 13.160540 | 44.55206 |
| 0.4963281 | 15.52624 | 16.603785 | 15.52637 |
| 0.6730395 | 21.05416 | 13.884786 | 21.05433 |
| 0.6830746 | 21.36808 | 6.502492 | 21.36826 |
| 1.0418474 | 32.59129 | 9.366898 | 32.59155 |
Derived Measures
Compare Values of $\alpha$ and $Q_0$ via Extra Sum-of-Squares F-Test
When one has multiple groups, it may be beneficial to compare whether separate curves are preferred over a single curve. This is accomplished by the Extra Sum-of-Squares F-test. This function (using the argument compare) will determine whether a single $\alpha$ or a single $Q_0$ is better than multiple $\alpha$s or $Q_0$s. A single curve will be fit, the residual deviations calculated and those residuals are compared to residuals obtained from multiple curves. A resulting F statistic will be reporting along with a p value.
## setting the seed initializes the random number generator so results will be
## reproducible
set.seed(1234)
## manufacture random grouping
apt$group <- NA
apt[apt$id %in% sample(unique(apt$id), length(unique(apt$id))/2), "group"] <- "a"
apt$group[is.na(apt$group)] <- "b"
## take a look at what the new groupings look like in long form
knitr::kable(apt[1:20, ])
| id | x | y | group |
|---|---|---|---|
| 19 | 0.0 | 10 | a |
| 19 | 0.5 | 10 | a |
| 19 | 1.0 | 10 | a |
| 19 | 1.5 | 8 | a |
| 19 | 2.0 | 8 | a |
| 19 | 2.5 | 8 | a |
| 19 | 3.0 | 7 | a |
| 19 | 4.0 | 7 | a |
| 19 | 5.0 | 7 | a |
| 19 | 6.0 | 6 | a |
| 19 | 7.0 | 6 | a |
| 19 | 8.0 | 5 | a |
| 19 | 9.0 | 5 | a |
| 19 | 10.0 | 4 | a |
| 19 | 15.0 | 3 | a |
| 19 | 20.0 | 2 | a |
| 30 | 0.0 | 3 | b |
| 30 | 0.5 | 3 | b |
| 30 | 1.0 | 3 | b |
| 30 | 1.5 | 3 | b |
## in order for this to run, you will have had to run the code immediately
## preceeding (i.e., the code to generate the groups)
ef <- ExtraF(dat = apt, equation = "koff", k = 2, groupcol = "group", verbose = TRUE)
[1] "Null hypothesis: alpha same for all data sets"
[1] "Alternative hypothesis: alpha different for each data set"
[1] "Conclusion: fail to reject the null hypothesis"
[1] "F(1,156) = 0.0298, p = 0.8631"
A summary table (broken up here for ease of display) will be created when the option verbose = TRUE. This table can be accessed as the dfres object resulting from ExtraF. In the example above, we can access this summary table using ef$dfres:
| Group | Q0d | K | R2 | Alpha |
|---|---|---|---|---|
| Shared | NA | NA | NA | NA |
| a | 8.489634 | 2 | 0.6206444 | 0.0040198 |
| b | 5.848119 | 2 | 0.6206444 | 0.0040198 |
| Not Shared | NA | NA | NA | NA |
| a | 8.503442 | 2 | 0.6448801 | 0.0040518 |
| b | 5.822075 | 2 | 0.5242825 | 0.0039376 |
Fitted Measures
| Group | N | AbsSS | SdRes |
|---|---|---|---|
| Shared | NA | NA | NA |
| a | 160 | 387.0945 | 1.570213 |
| b | 160 | 387.0945 | 1.570213 |
| Not Shared | NA | NA | NA |
| a | 80 | 249.2764 | 1.787695 |
| b | 80 | 137.7440 | 1.328890 |
Uncertainty and Model Information
| Group | EV | Omaxd | Pmaxd |
|---|---|---|---|
| Shared | NA | NA | NA |
| a | 0.8795301 | 22.63159 | 8.453799 |
| b | 0.8795301 | 22.63159 | 12.272265 |
| Not Shared | NA | NA | NA |
| a | 0.8725741 | 22.45260 | 8.373320 |
| b | 0.8978945 | 23.10414 | 12.584550 |
Derived Measures
| Group | Omaxa | Notes |
|---|---|---|
| Shared | NA | NA |
| a | 22.63190 | converged |
| b | 22.63190 | converged |
| Not Shared | NA | NA |
| a | 22.45291 | converged |
| b | 23.10445 | converged |
Convergence and Summary Information
When verbose = TRUE, objects from the result can be used in subsequent graphing. The following code generates a plot of our two groups. We can use the predicted values already generated from the ExtraF function by accessing the newdat object. In the example above, we can access these predicted values using ef$newdat. Note that we keep the linear scaling of y given we used Koffarnus et al. (2015)’s equation fitted to the data.
## be sure that you've loaded the tidyverse package (e.g., library(tidyverse))
ggplot(apt, aes(x = x, y = y, group = group)) +
## the predicted lines from the sum of squares f-test can be used in subsequent
## plots by calling data = ef$newdat
geom_line(aes(x = x, y = y, group = group, color = group),
data = ef$newdat[ef$newdat$x >= .1, ]) +
stat_summary(fun.data = mean_se, aes(width = .05, color = group),
geom = "errorbar") +
stat_summary(fun.y = mean, aes(fill = group), geom = "point", shape = 21,
color = "black", stroke = .75, size = 4) +
scale_x_log10(limits = c(.4, 50), breaks = c(.1, 1, 10, 100)) +
scale_color_discrete(name = "Group") +
scale_fill_discrete(name = "Group") +
labs(x = "Price per Drink", y = "Drinks Purchased") +
theme(legend.position = c(.85, .75)) +
## theme_apa is a beezdemand function used to change the theme in accordance
## with American Psychological Association style
theme_apa()
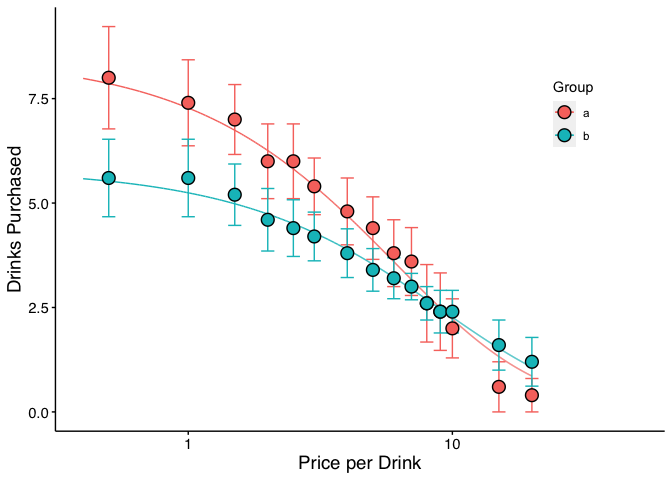
Plots
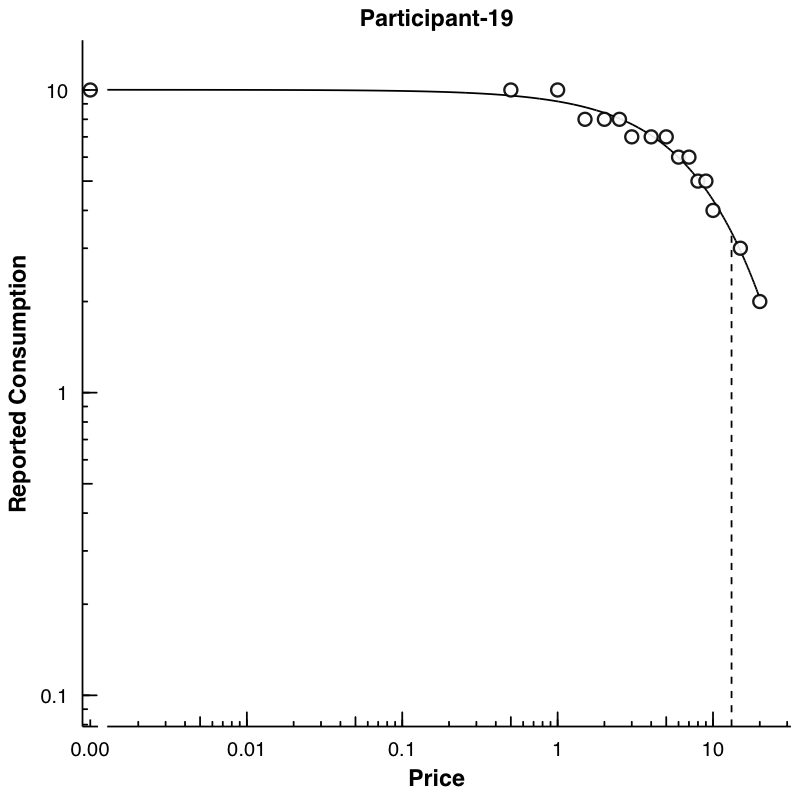
Plots can be created using the PlotCurves function. This function takes the output from FitCurves when the argument from FitCurves, detailed = TRUE. The default will be to save figures into a plots folder created one directory above the current working directory. Figures can be saved as either PNG or PDF. If the argument ask = TRUE, then plots will be shown interactively and not saved (ask = FALSE is the default). Graphs can automatically be created at both an aggregate and individual level.
As a demonstration, let’s first use FitCurves on the apt dataset, specifying k = "share" and detailed = T. This will return a list of objects to use in PlotCurves. In PlotCurves, we will feed in our new object, out, and tell the function to save the plots in the directory "../plots/" and ask = FALSE because we don’t want R to interactively show us each plot. Because we have 10 datasets in our apt example, 10 plots will be created and saved in the "../plots/" directory.
out <- FitCurves(dat = apt, equation = "hs", k = "share", detailed = T)
Warning: Zeros found in data not compatible with equation! Dropping zeros!
Beginning search for best-starting k
Best k fround at 0.93813356574003 = err: 0.744881846162718
Searching for shared K, this can take a while...
PlotCurves(dat = out, outdir = plotdir, device = "png", ask = F)
10 plots saved in man/figures/
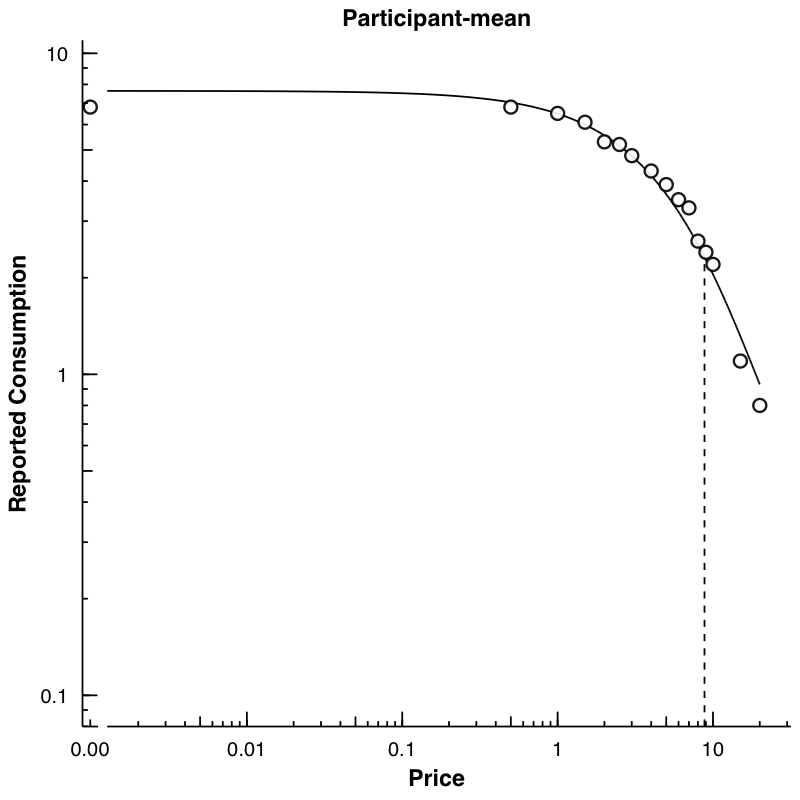
We can also make a plot of the mean data. Here, we again use FitCurves, this time calculating a k from the observed range of the data (thus not specifying any k) and specifying agg = "Mean".
mn <- FitCurves(dat = apt, equation = "hs", agg = "Mean", detailed = T)
No k value specified. Defaulting to empirical mean range +.5
PlotCurves(dat = mn, outdir = plotdir, device = "png", ask = F)
1 plots saved in man/figures/
list.files("../plots/")
[1] "Participant-106.png" "Participant-113.png" "Participant-142.png"
[4] "Participant-156.png" "Participant-188.png" "Participant-19.png"
[7] "Participant-30.png" "Participant-38.png" "Participant-60.png"
[10] "Participant-68.png" "Participant-mean.png"
Learn More About Functions
To learn more about a function and what arguments it takes, type “?” in front of the function name.
?CheckUnsystematic
CheckUnsystematic package:beezdemand R Documentation
Systematic Purchase Task Data Checker
Description:
Applies Stein, Koffarnus, Snider, Quisenberry, & Bickels (2015)
criteria for identification of nonsystematic purchase task data.
Usage:
CheckUnsystematic(dat, deltaq = 0.025, bounce = 0.1, reversals = 0,
ncons0 = 2)
Arguments:
dat: Dataframe in long form. Colums are id, x, y.
deltaq: Numeric vector of length equal to one. The criterion by which
the relative change in quantity purchased will be compared.
Relative changes in quantity purchased below this criterion
will be flagged. Default value is 0.025.
bounce: Numeric vector of length equal to one. The criterion by which
the number of price-to-price increases in consumption that
exceed 25% of initial consumption at the lowest price,
expressed relative to the total number of price increments,
will be compared. The relative number of price-to-price
increases above this criterion will be flagged. Default value
is 0.10.
reversals:Numeric vector of length equal to one. The criterion by
which the number of reversals from number of consecutive (see
ncons0) 0s will be compared. Number of reversals above this
criterion will be flagged. Default value is 0.
ncons0: Number of consecutive 0s prior to a positive value is used to
flag for a reversal. Value can be either 1 (relatively more
conservative) or 2 (default; as recommended by Stein et al.,
(2015).
Details:
This function applies the 3 criteria proposed by Stein et al.,
(2015) for identification of nonsystematic purchase task data. The
three criteria include trend (deltaq), bounce, and reversals from
0. Also reports number of positive consumption values.
Value:
Dataframe
Author(s):
Brent Kaplan <[email protected]>
Examples:
## Using all default values
CheckUnsystematic(apt, deltaq = 0.025, bounce = 0.10, reversals = 0, ncons0 = 2)
## Specifying just 1 zero to flag as reversal
CheckUnsystematic(apt, deltaq = 0.025, bounce = 0.10, reversals = 0, ncons0 = 1)
Acknowledgments
Shawn P. Gilroy, Contributor GitHub
Derek D. Reed, Applied Behavioral Economics Laboratory
Mikhail N. Koffarnus, Addiction Recovery Research Center
Steven R. Hursh, Institutes for Behavior Resources, Inc.
Paul E. Johnson, Center for Research Methods and Data Analysis, University of Kansas
Peter G. Roma, Institutes for Behavior Resources, Inc.
W. Brady DeHart, Addiction Recovery Research Center
Michael Amlung, Cognitive Neuroscience of Addictions Laboratory
Special thanks to the following people who helped provide feedback on this document:
Alexandra M. Mellis
Mr. Jeremiah “Downtown Jimbo Brown” Brown
Gideon Naudé
Recommended Readings
Reed, D. D., Niileksela, C. R., & Kaplan, B. A. (2013). Behavioral economics: A tutorial for behavior analysts in practice. Behavior Analysis in Practice, 6 (1), 34–54. https://doi.org/10.1007/BF03391790
Reed, D. D., Kaplan, B. A., & Becirevic, A. (2015). Basic research on the behavioral economics of reinforcer value. In Autism Service Delivery (pp. 279-306). Springer New York. https://doi.org/10.1007/978-1-4939-2656-5_10
Hursh, S. R., & Silberberg, A. (2008). Economic demand and essential value. Psychological Review, 115 (1), 186-198. https://dx.doi.org/10.1037/0033-295X.115.1.186
Koffarnus, M. N., Franck, C. T., Stein, J. S., & Bickel, W. K. (2015). A modified exponential behavioral economic demand model to better describe consumption data. Experimental and Clinical Psychopharmacology, 23 (6), 504-512. https://dx.doi.org/10.1037/pha0000045
Stein, J. S., Koffarnus, M. N., Snider, S. E., Quisenberry, A. J., & Bickel, W. K. (2015). Identification and management of nonsystematic purchase task data: Toward best practice. Experimental and Clinical Psychopharmacology 23 (5), 377-386. https://dx.doi.org/10.1037/pha0000020
Hursh, S. R., Raslear, T. G., Shurtleff, D., Bauman, R., & Simmons, L. (1988). A cost‐benefit analysis of demand for food. Journal of the Experimental Analysis of Behavior, 50 (3), 419-440. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1338908/