Deal with Bratteli Graphs.

bratteli

Bratteli graphs.

This package deals with Bratteli graphs. In every function of the package, the Bratteli graph is given by a function returning for a level n of the graph the incidence matrix of the graph between level n and level n+1: the (i,j)-entry of this matrix is the number of edges between the i-th vertex at level n and the j-th vertex at level n+1.

For example, the binary tree is defined by:

tree <- function(n) {
  M <- matrix(0, nrow = 2^n, ncol = 2^(n+1))
  for(i in 1:nrow(M)) {
    M[i, ][c( 2*(i-1)+1, 2*(i-1)+2 )] <- 1
  }
  M
}

The function bratteliGraph generates some LaTeX code which renders the graph up to a given level:

bratteliGraph("binaryTree.tex", tree, 3)

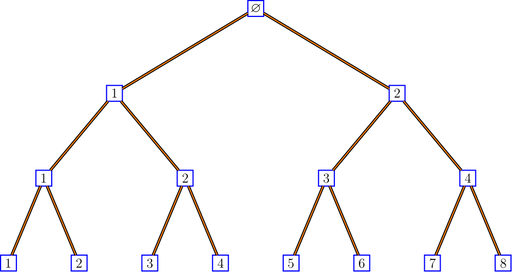
If you don’t like the style, you are free to modify the LaTeX code.

Here is a binary tree with double edges:

tree2 <- function(n) {
  M <- matrix(0, nrow = 2^n, ncol = 2^(n+1))
  for(i in 1:nrow(M)) {
    M[i, ][c( 2*(i-1)+1, 2*(i-1)+2 )] <- 2
  }
  M
}
bratteliGraph("binaryTree2.tex", tree2, 3)

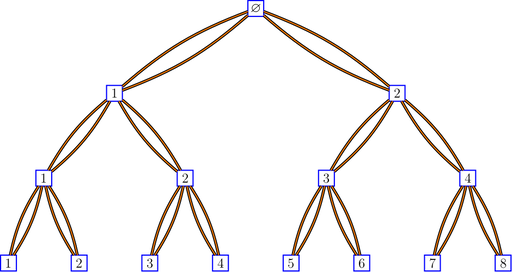
Here is the code for the Pascal graph:

Pascal <- function(n) {
  M <- matrix(0, nrow = n+1, ncol = n+2)
  for(i in 1:(n+1)) {
    M[i, ][c( i, i+1L )] <- 1
  }
  M
}

The dimension of a vertex of a Bratteli graph is the number of paths of the graph going from the root vertex to this vertex. The function bratteliDimensions of the package computes these numbers:

library(bratteli)
bratteliDimensions(Pascal, 3)

## [[1]]
## [1] "1" "1"
## 
## [[2]]
## [1] "1" "2" "1"
## 
## [[3]]
## [1] "1" "3" "3" "1"

Bratteli graphs are of interest to ergodicians, and particularly to Vershik, who introduced the intrinsic kernels of a Bratteli graph and the intrinsic distance between the vertices of a Bratteli graph. Here is a picture of the Pascal graph showing the intrinsic kernels:

bratteliGraph("Pascal.tex", Pascal, 3, edgelabels = "kernels")

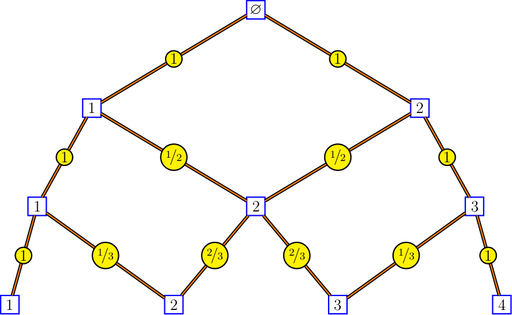
The intrinsic kernels are returned by the function bratteliKernels. The intrinsic distances between two vertices at the same level are returned by the function bratteliDistances.