Marginal Survival Estimation with Covariate Adjustment.

bunsen: Marginal Estimation with Covariate Adjustment for Survival Endpoint in Clinical Trials

The bunsen package aims to provide an easy-to-use interface for estimating marginal or unconditional Hazard Ratio (HR) and Restricted Mean Survival Time (RMST) when adjusting prognostic covariates in clinical trials.

Key features

We introduce bunsen package for marginal HR and RMST estimation and variance for time-to-event endpoints in clinical trials. We included multiple features in current package:

• Marginal HR estimation
  • Rcpp (C++) optimization
  • ClusterMQ parallel computation
    • Local multiprocess and multicores parallel computation for point estimate (suggested)
    • LSF parallel computation for point estimate
    • LSF and/or nested local multiprocess parallel computation for variance (suggested)
• RMST estimation

Package architecture

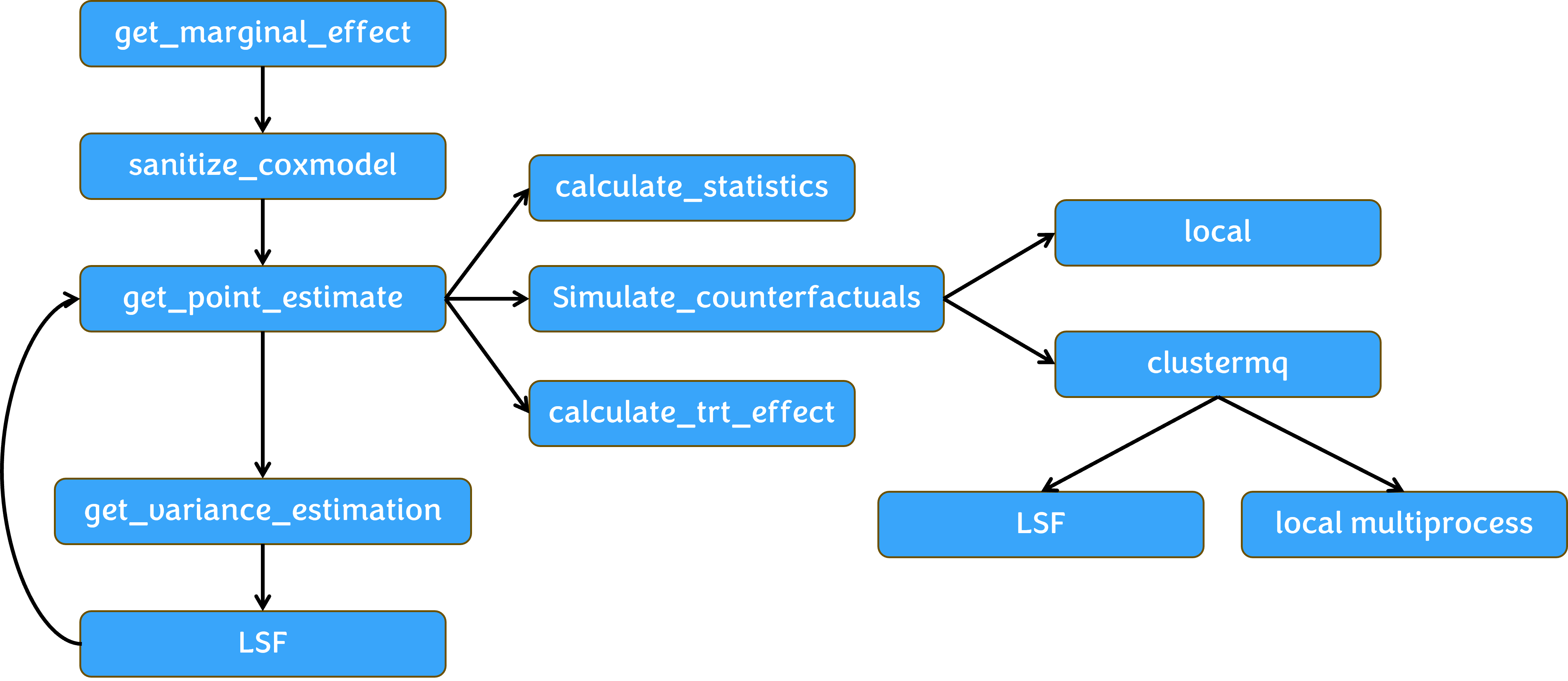
Example

Marginal point estimate and variance of HR for COX model

library(bunsen)

data('oak')

cox_event <- coxph(Surv(OS, os.status) ~ trt+btmb+pdl1, data=oak)

cox_censor <- coxph(Surv(OS, 1-os.status) ~trt+btmb+pdl1, data=oak)

result=get_marginal_effect(trt = 'trt',cox_event,cox_censor,M=10000,data=oak,seed = 1)
# Calculating point estimate in local clustermq using multiprocess...
# Submitting 4 worker jobs (ID: cmq7488) ...
# Running 4 calculations (8 objs/120.1 Kb common; 1 calls/chunk) ...
# Master: [8.6 secs 0.8% CPU]; Worker: [avg 19.1% CPU, max 303.9 Mb]                                                                                              
# Calculating SE in clustermq using bootstrap N = 1000...
# Submitting 100 worker jobs (ID: cmq9642) ...
# Running 1,000 calculations (14 objs/354.8 Kb common; 1 calls/chunk) ...
# Master: [16.0 secs 8.4% CPU]; Worker: [avg 48.5% CPU, max 307.7 Mb] 

result
# Call:
# Surv(OS, os.status) ~ trt + btmb + pdl1
# Marginal treatment effect calculated by N = 10000 simulations
# Number of sample: 578 
#             coef        exp(coef)   se(coef)    2.5%        97.5%     
# trt         -0.442910   0.642165    0.103905    -0.654306   -0.245416 
# clustermq setting:
#  number of remote workers =  100 , each worker has 1 core(s)
# Point estimate: parallel computation (clustermq)
# SE (bootstrap): parallel computation
# 95%CI estimated by bootstrap

summary(result)

# Call:
# Surv(OS, os.status) ~ trt + btmb + pdl1
# Marginal treatment effect calculated by N = 10000 simulations
# Treatment variable: trt ------ Number of sample: 578 
# Number of events in cox_event: 423 
# Number of events in cox_censor: 155 
# Random seed =  1 
# Original treatment effect:
#             coef        exp(coef)   se(coef)    z           Pr(>|z|)  
# trt         -0.452408   0.636095    0.098428    -4.596346   0.000004  
# Marginal treatment effect:
#             coef        exp(coef)   se(coef)    z           Pr(>|z|)  
# trt         -0.442910   0.642165    0.103905    -4.262646   0.000020  
# 95% CI of Marginal treatment effect (bootstrap): -0.654 , -0.245

Marginal point estimate and variance of RMST for COX model

library(bunsen)

data('oak')

tau=26

time=oak$OS

status=oak$os.status

trt=oak$trt

covariates=oak[,c('btmb','pdl1')]

result=get_rmst_estimate(time, status, trt, covariates, tau, SE = "delta")

result
# Call:
# Surv(time, status) ~ btmb + pdl1 + strata(trt) 
# Restricted survival time: 26 
#             coef        se(coef)    2.5%        97.5%     
# trt         3.265971    0.716351    1.861923    4.670019  
# Method for SE calculation: delta

result=get_rmst_estimate(time, status, trt, covariates, tau, SE = "boot", seed = 2025)

result

# Call:
# Surv(time, status) ~ btmb + pdl1 + strata(trt) 
# Restricted survival time: 26 
#             coef        se(coef)    2.5%        97.5%     
# trt         3.265971    0.715191    1.994362    4.699867  
# Method for SE calculation: bootNumber of bootstrap: 1000 , random seed = 2025

Methodology

bunsen is developed based on three key papers:

• HR: Rhian Daniel et al. (2020)
• RMST: Theodore Karrison et al. (2018)
• Extension of above two methods: Jiawei Wei et al. (2024)

Package authors

• Xinlei Deng (Maintainer)
• Mark Baillie
• Dominic Magirr
• Craig Wang
• Alexander Przybylski

Acknowledgements

• Jiawei Wei
• Lukas Andreas Widmer.