Local Polynomial Regression of State Dependent Covariates in State-Space Models.
covafillr: Local Polynomial Regression of State Dependent Covariates in State-Space Models
## knitr settings
library(knitr)
opts_knit$set(root.dir=normalizePath('./'))
opts_chunk$set(fig.path = "./tools/README_fig/", dev='png')
Installing
covafillr version can be installed from CRAN with
install.packages("covafillr")
The development version of covafillr can be installed with
devtools::install_github("calbertsen/covafillr")
Installing with JAGS
To use covafillr with JAGS, JAGS must be installed before the covafillr package, and the package must be installed using the same compiler as JAGS is installed with.
On Unix(-like) systems, pkg-config is used to find the relevant paths to compile covafillr against JAGS, such as
pkg-config --cflags jags
pkg-config --libs jags
## -I/usr/local/include/JAGS
## -L/usr/local/lib -ljags
The package will only be installed with the JAGS module if the configure argument --with-jags is given. Note that the package must be compiled with the same compiler as JAGS.
On Windows, the R package rjags is used to find the paths. covafillr can be installed without using rjags by setting a system variable JAGS_ROOT to the folder where JAGS is installed, e.g., by running
Sys.setenv(JAGS_ROOT='C:/Program Files/JAGS/JAGS-4.1.0')
before installation. Similar to Unix(-like) systems, the package is only installed with the JAGS module if the system variable USE_JAGS is set, e.g., by running
Sys.setenv(USE_JAGS='yes')
Simple examples
Note that more examples are available in the inst/examples folder.
Using from R
library(methods)
library(covafillr)
The package can be used from R to do local polynomial regression and a search tree approximation of local polynomial regression. Both are implemented with reference classes.
Local polynomial regression
The reference class for local polynomial regression is called covafill.
methods::getRefClass('covafill')
## Generator for class "covafill":
##
## Class fields:
##
## Name: ptr
## Class: externalptr
## Locked Fields: "ptr"
##
##
## Class Methods:
## "import", "getDegree", ".objectParent", "setBandwith", "residuals",
## "usingMethods", "show", "getClass", "untrace", "export",
## "copy#envRefClass", "initialize", ".objectPackage", "callSuper",
## "getDim", "copy", "getBandwith", "predict", "initFields",
## "getRefClass", "trace", "field"
##
## Reference Superclasses:
## "envRefClass"
To illustrate the usage we simulate data.
fn <- function(x) x ^ 4 - x ^ 2
x <- runif(2000,-10,10)
y <- fn(x) + rnorm(2000,0,0.1)
An object of the reference class is created by
cf <- covafill(coord = x,obs = y,p = 5L)
where p is the polynomial degree. The bandwith can be set by the argument h. By default, a value is suggested by the function suggestBandwith. Information about the class can be extracted (and changed) by the following functions:
cf$getDim()
## [1] 1
cf$getDegree()
## [1] 5
cf$getBandwith()
## [1] 15.2975
cf$setBandwith(1.0)
## [1] 1
cf$getBandwith()
## [1] 1
To do local polynomial regression at a point, the $predict function is used.
x0 <- seq(-3,3,0.1)
y0 <- cf$predict(x0)
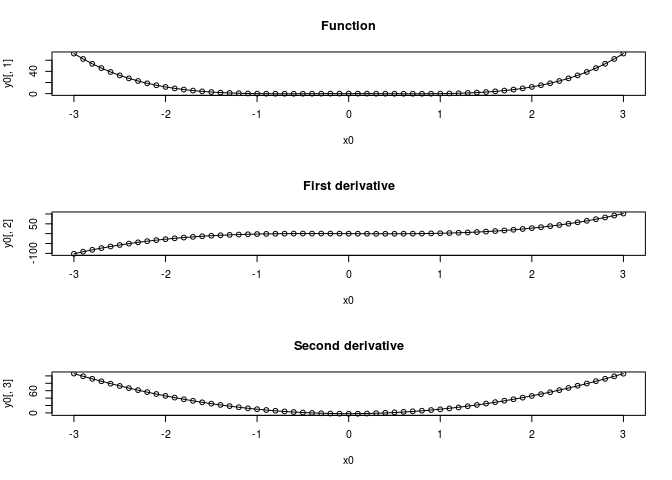
The function returns a matrix of estimated function values and derivatives.
par(mfrow=c(3,1))
plot(x0,y0[,1], main = "Function")
lines(x0,fn(x0))
plot(x0, y0[,2], main = "First derivative")
lines(x0, 4 * x0 ^ 3 - 2 * x0)
plot(x0, y0[,3], main = "Second derivative")
lines(x0, 3 * 4 * x0 ^ 2 - 2)
Search tree approximation
The reference class for search tree approximation to local polynomial regression is covatree
methods::getRefClass('covatree')
## Generator for class "covatree":
##
## Class fields:
##
## Name: ptr
## Class: externalptr
## Locked Fields: "ptr"
##
##
## Class Methods:
## "import", ".objectParent", "usingMethods", "show", "getClass",
## "untrace", "export", "copy#envRefClass", "initialize",
## ".objectPackage", "callSuper", "getDim", "copy", "predict",
## "initFields", "getRefClass", "trace", "field"
##
## Reference Superclasses:
## "envRefClass"
covatree has an aditional argument, minLeft, which is the minimum number of observations at which a sub tree will be created. Otherwise the functionality is similar.
ct <- covatree(coord = x,obs = y,p = 5L, minLeft = 50)
ct$getDim()
## [1] 1
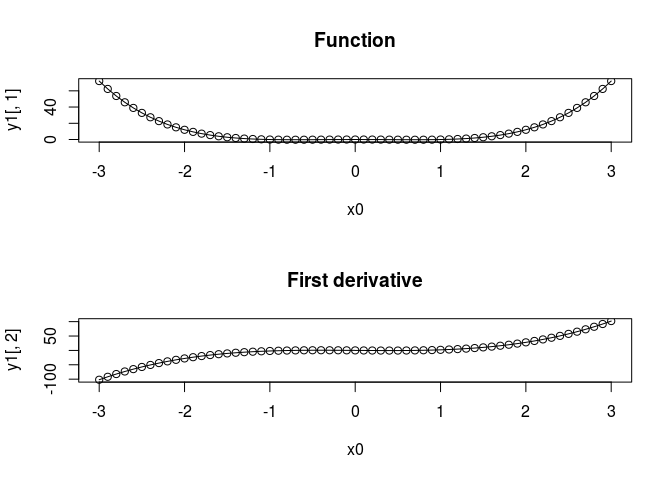
y1 <- ct$predict(x0)
par(mfrow=c(2,1))
plot(x0,y1[,1], main = "Function")
lines(x0,fn(x0))
plot(x0, y1[,2], main = "First derivative")
lines(x0, 4 * x0 ^ 3 - 2 * x0)
Using with Rcpp/inline
The covafillr package provides a plugin for inline.
library(inline)
The following code does local polynomial regression at the point x based on the observations obs at the points coord. For convenience, the plugin provides the type definitions cVector and cMatrix to pass to the covafill constructor and operator.
cftest <- '
cVector x1 = as<cVector>(x);
cMatrix coord1 = as<cMatrix>(coord);
cVector obs1 = as<cVector>(obs);
int p1 = as<int>(p);
cVector h1 = as<cVector>(h);
covafill<double> cf(coord1,obs1,h1,p1);
return wrap(cf(x1));'
An R function can now be defined with inlined C++ code using plugin='covafillr'.
fun <- cxxfunction(signature(x='numeric',
coord = 'matrix',
obs = 'numeric',
p = 'integer',
h = 'numeric'),
body = cftest,
plugin = 'covafillr'
)
fun(c(0),matrix(x,ncol=1),y,2,1.0)
## [1] -0.03907458 -0.01879995
Using with TMB
To use covafillr with TMB, include covafill/TMB in the beginning of the cpp file.
// tmb_covafill.cpp
#include <TMB.hpp>
#include <covafill/TMB>
template<class Type>
Type objective_function<Type>::operator() ()
{
DATA_MATRIX(coord);
DATA_VECTOR(covObs);
DATA_INTEGER(p);
DATA_VECTOR(h);
PARAMETER_VECTOR(x);
covafill<Type> cf(coord,covObs,h,p);
Type val = evalFill((CppAD::vector<Type>)x, cf)[0];
return val;
}
Instead of calling the usual operator, the covafill object is evaluated at a point with the evalFill function. This function enables TMB to use the estimated gradient in the automatic differentiation.
From R, the cpp file must be compiled with additional flags as seen below.
library(TMB)
TMB::compile('tmb_covafill.cpp',CXXFLAGS = cxxFlags())
## Note: Using Makevars in /home/cmoe/.R/Makevars
## [1] 0
dyn.load(dynlib("tmb_covafill"))
Then TMB can be used as usual.
dat <- list(coord = matrix(x,ncol=1),
covObs = y,
p = 2,
h = 1.0)
obj <- MakeADFun(data = dat,
parameters = list(x = c(0)),
DLL = "tmb_covafill")
obj$fn(c(3.2))
## [1] 94.50085
obj$fn(c(0))
## [1] -0.03907458
obj$fn(c(-1))
## [1] -0.05840993
obj$gr()
## outer mgc: 3.661488
## [,1]
## [1,] -3.661488
Using with rjags
library(rjags)
## Loading required package: coda
## Linked to JAGS 4.0.0
## Loaded modules: basemod,bugs
If covafillr is installed with JAGS, a module is compiled with the package. The module can be loaded in R by the function loadJAGSModule, a wrapper for rjags::load.module.
loadJAGSModule()
## module covafillr loaded
Then the function covafill is available to use in the JAGS code
# covafill.jags
model {
cf <- covafill(x,obsC,obs,h,2.0)
sigma ~ dunif(0,100)
tau <- pow(sigma, -2)
for(i in 1:N) {
y[i] ~ dnorm(cf[i],tau)
}
}
fun <- function(x) x ^ 2
n <- 100
x <- runif(n,-2,2)
y <- rnorm(n,fun(x),0.5)
obsC <- seq(-3,3,len=1000)
obs <- fun(obsC) + rnorm(length(obsC),0,0.1)
Then rjags can be used as usual.
jags <- jags.model('covafill.jags',
data = list(N = n,
x = matrix(x,ncol=1),
y = y,
obsC = matrix(obsC,ncol=1),
obs = obs,
h = c(1)),
n.chains = 1,
n.adapt = 100)
## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 100
## Unobserved stochastic nodes: 1
## Total graph size: 2314
##
## Initializing model
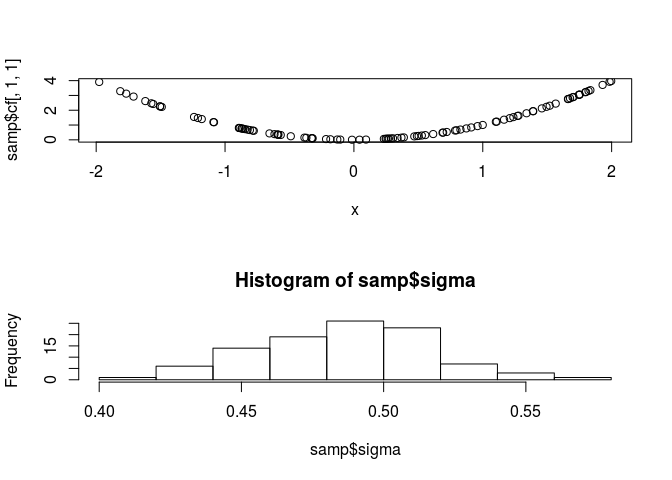
samp <- jags.samples(jags,c('sigma','cf'),n.iter = 1000, thin = 10)
par(mfrow=c(2,1))
plot(x,samp$cf[,1,1])
hist(samp$sigma)