Description
Generate and Simulate Deterministic Discrete-Time Compartmental Models.
Description
R package to build and simulate deterministic discrete-time compartmental models that can be non-Markov. Length of stay in each compartment can be defined to follow a parametric distribution (d_exponential(), d_gamma(), d_weibull(), d_lognormal()) or a non-parametric distribution (nonparametric()). Other supported types of transition from one compartment to another includes fixed transition (constant()), multinomial (multinomial()), fixed transition probability (transprob()).
README.md
denim 
An R package for building and simulating deterministic discrete-time compartmental models with memory.
Installation
You can install the development version of denim from GitHub with:
# install.packages("devtools")
devtools::install_github("thinhong/denim")
Example
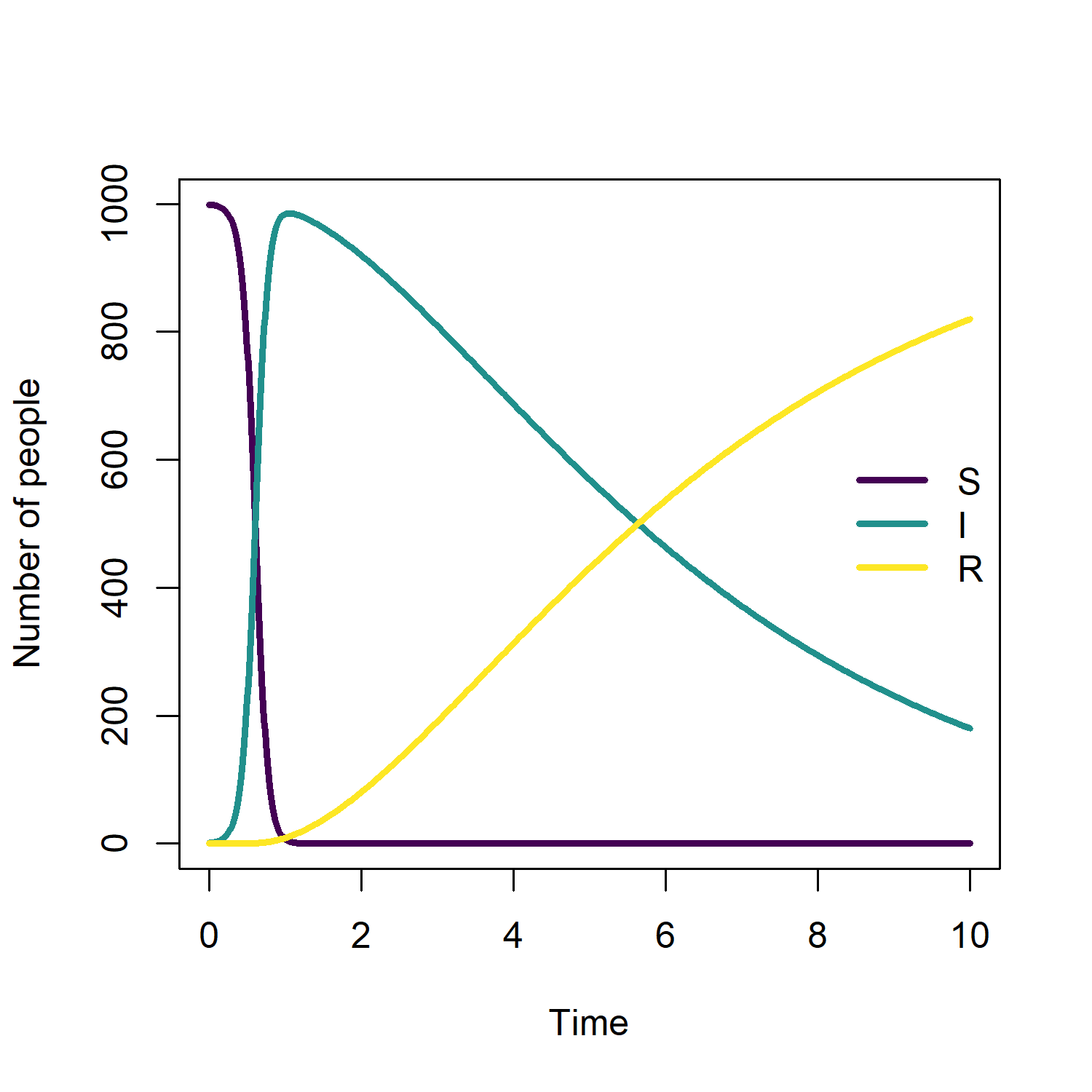
This is a basic example to illustrate the specification of a simple SIR model, which contains three compartments susceptible (S), infected (I) and recovered (R). The recovery probabilities of infected individuals are gamma distributed in this example:
library(denim)
transitions <- list(
"S -> I" = "beta * S * I / N",
"I -> R" = d_gamma(3, 2)
)
parameters <- c(
beta = 0.12,
N = 1000
)
initialValues <- c(
S = 999,
I = 1,
R = 0
)
simulationDuration <- 10
timeStep <- 0.01
mod <- sim(transitions = transitions, initialValues = initialValues,
parameters = parameters, simulationDuration = simulationDuration,
timeStep = timeStep)
The output is a data frame with 4 columns: Time, S, I and R
head(mod)
#> Time S I R
#> 1 0.00 999.0000 1.000000 0.000000e+00
#> 2 0.01 998.8801 1.119874 5.543225e-06
#> 3 0.02 998.7459 1.254092 2.278823e-05
#> 4 0.03 998.5956 1.404364 5.306419e-05
#> 5 0.04 998.4273 1.572606 9.785981e-05
#> 6 0.05 998.2389 1.760961 1.588423e-04
We can plot the output with:
plot(mod)