Forensic Pedigree Analysis and Relatedness Inference.

forrel

Introduction

The goal of forrel is to provide forensic pedigree computations and relatedness inference from genetic marker data. The forrel package is part of the pedsuite, a collection of R packages for pedigree analysis.

The most important analyses currently supported by forrel are:

• Likelihood ratio (LR) computations for relationship testing
• Pairwise relatedness inference: Estimation of IBD coefficients (both $\kappa$ and $\Delta$) from marker data
• Visualisation of IBD coefficients in the IBD triangle
• Simulation of marker genotypes. Unconditional or conditional on known genotypes
• Power analysis for relationship testing: LR distributions, exclusion power (EP) and inclusion power (IP)
• Tailor-made functions for power analysis in family reunion cases:
  • missingPersonPlot()
  • missingPersonEP()
  • missingPersonIP()
  • MPPsims()
  • powerPlot()
• Import of pedigree data and frequency databases from the Familias software.

Installation

To get the current official version of forrel, install from CRAN as follows:

install.packages("forrel")

Alternatively, you can obtain the latest development version from GitHub:

# install.packages("devtools") # install devtools if needed
devtools::install_github("magnusdv/forrel")

An example

In this short introduction, we first demonstrate simulation of marker data for a pair of siblings. Then - pretending the relationship is unknown to us - we estimate the relatedness between the brothers using the simulated data. If all goes well, the estimate should be close to the expected value for siblings.

library(forrel)
#> Loading required package: pedtools

Create the pedigree

We start by creating and plotting a pedigree with two brothers, named bro1 and bro2.

x = nuclearPed(children = c("bro1", "bro2"))
plot(x)

Marker simulation

Now let us simulate the genotypes of 100 independent SNPs for all four family members. Each SNP has alleles 1 and 2, with equal frequencies by default. This is an example of unconditional simulation, since we don’t give any genotypes to condition on.

x = markerSim(x, N = 100, alleles = 1:2, seed = 1234)
#> Unconditional simulation of 100 autosomal markers.
#> Individuals: 1, 2, bro1, bro2
#> Allele frequencies:
#>    1   2
#>  0.5 0.5
#> Mutation model: No 
#> 
#> Simulation finished.
#> Calls to `likelihood()`: 0.
#> Total time used: 0.11 seconds.

Note 1: The seed argument is passed onto the random number generator. If you use the same seed, you should get exactly the same results.
Note 2: To suppress the informative messages printed during simulation, add verbose = FALSE to the function call.

The pedigree x now has 100 markers attached to it. The genotypes of the first few markers are shown when printing x to the screen:

x
#>    id fid mid sex <1> <2> <3> <4> <5>
#>     1   *   *   1 1/2 1/2 1/1 2/2 2/2
#>     2   *   *   2 1/1 1/2 1/1 1/1 2/2
#>  bro1   1   2   1 1/1 1/2 1/1 1/2 2/2
#>  bro2   1   2   1 1/1 1/2 1/1 1/2 2/2
#> Only 5 (out of 100) markers are shown.

Conditional simulation

Suppose one of the brothers is homozygous 1/1 and that we want to simulate genotypes for the other brother. This is achieved with the following code, where after first attaching a marker to the pedigree, specifying the known genotype, we condition on it by referencing it in markerSim().

y = nuclearPed(children = c("bro1", "bro2")) |> 
  addMarker(bro1 = "1/1", alleles = 1:2, name = "snp1") |> 
  markerSim(N = 100, ids = "bro2", partialmarker = "snp1", 
            seed = 321, verbose = FALSE)
y
#>    id fid mid sex <1> <2> <3> <4> <5>
#>     1   *   *   1 -/- -/- -/- -/- -/-
#>     2   *   *   2 -/- -/- -/- -/- -/-
#>  bro1   1   2   1 1/1 1/1 1/1 1/1 1/1
#>  bro2   1   2   1 2/2 1/2 1/1 1/1 1/1
#> Only 5 (out of 100) markers are shown.

Note that the previous code also demonstrates how pedsuite is well adapted to the R pipe |>.

Estimation of IBD coefficients

The ibdEstimate() function estimates the coefficients of identity-by-descent (IBD) between pairs of individuals, from the available marker data. Let us try with the simulated genotypes we just generated:

k = ibdEstimate(y, ids = c("bro1", "bro2"))
#> Estimating 'kappa' coefficients
#> Initial search value: (0.333, 0.333, 0.333)
#> Pairs of individuals: 1
#>   bro1 vs. bro2: estimate = (0.28, 0.54, 0.18), iterations = 10
#> Total time: 0.00928 secs
k
#>    id1  id2   N      k0      k1      k2
#> 1 bro1 bro2 100 0.28001 0.53998 0.18001

To get a visual sense of the estimate, it is instructive to plot it in the IBD triangle:

showInTriangle(k, labels = TRUE)

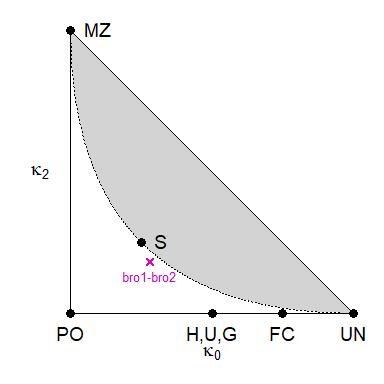
Reassuringly, the estimate is close to the theoretical expectation for non-inbred full siblings, $(\kappa_0, \kappa_1, \kappa_2) = (0.25, 0.5, 0.25)$, corresponding to the point marked S in the triangle.