Description
Generalized Linear Models with Truncated Lasso Penalty.
Description
Extremely efficient procedures for fitting regularization path with l0, l1, and truncated lasso penalty for linear regression and logistic regression models. This version is a completely new version compared with our previous version, which was mainly based on R. New core algorithms are developed and are now written in C++ and highly optimized.
README.md
glmtlp
The goal of glmtlp is to fit generalized linear models with l0, l1 and truncated lasso penalty with a fast procedure.
Installation
You can install the released version of glmtlp from CRAN with:
install.packages("glmtlp")
Examples for Gaussian Regression Models
The following are three examples which show you how to use glmtlp to fit gaussian regression models:
library(glmtlp)
data("gau_data")
colnames(gau_data$X)[gau_data$beta != 0]
#> [1] "V1" "V6" "V10" "V15" "V20"
# Cross-Validation using TLP penalty
cv.fit <- cv.glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "tlp", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V1 V6 V10 V15 V20
#> -0.009692127 1.240201054 0.883169910 0.725706771 1.125980744 0.981390567
plot(cv.fit)
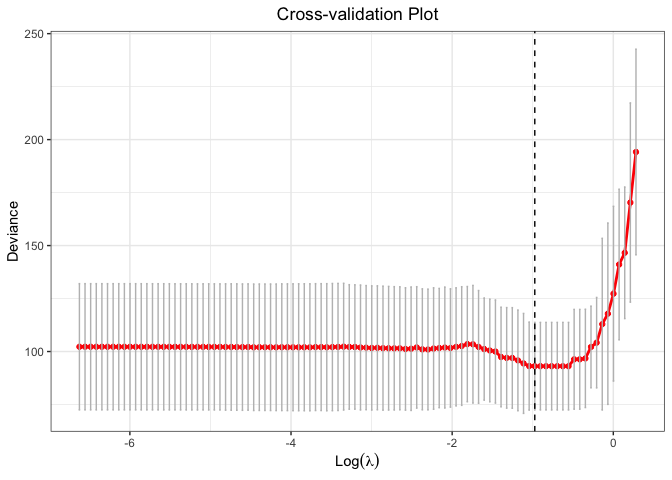
# Single Model Fit using TLP penalty
fit <- glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "tlp")
coef(fit, lambda = cv.fit$lambda.min)
#> intercept V1 V2 V3 V4 V5
#> -0.009692127 1.240201054 0.000000000 0.000000000 0.000000000 0.000000000
#> V6 V7 V8 V9 V10 V11
#> 0.883169910 0.000000000 0.000000000 0.000000000 0.725706771 0.000000000
#> V12 V13 V14 V15 V16 V17
#> 0.000000000 0.000000000 0.000000000 1.125980744 0.000000000 0.000000000
#> V18 V19 V20
#> 0.000000000 0.000000000 0.981390567
predict(fit, X = gau_data$X[1:5, ], lambda = cv.fit$lambda.min)
#> [1] 0.1906169 2.2279315 -1.4255560 0.9313560 -2.8151758
plot(fit, xvar = "log_lambda", label = TRUE)
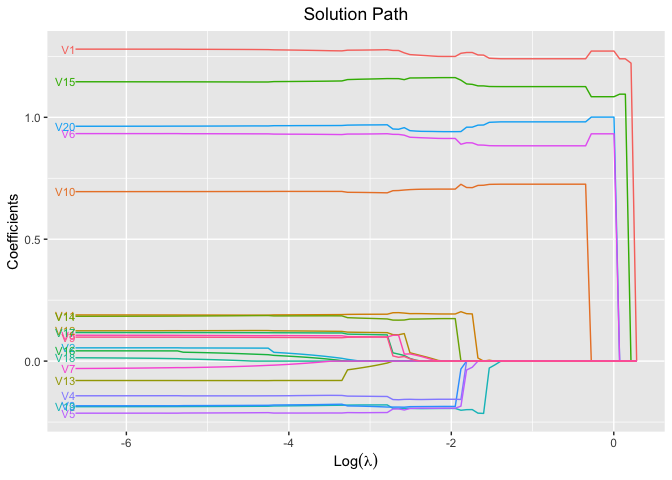
# Cross-Validation using L0 penalty
cv.fit <- cv.glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "l0", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V1 V6 V10 V15 V20
#> -0.009687042 1.240319880 0.883378583 0.725607300 1.125958218 0.981544178
plot(cv.fit)
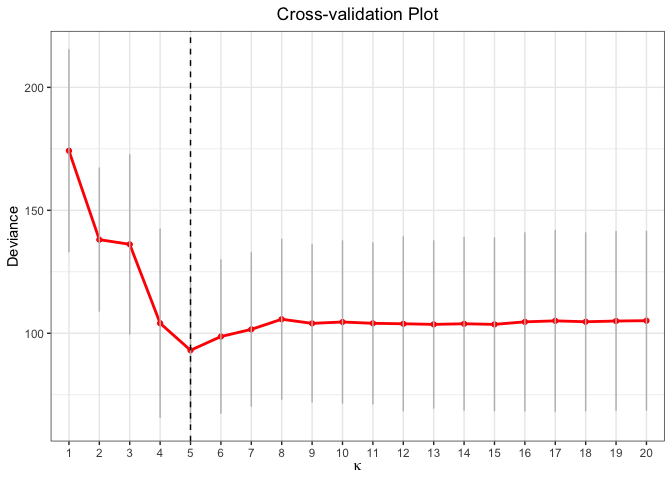
# Single Model Fit using L0 penalty
fit <- glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "l0")
coef(fit, kappa = cv.fit$kappa.min)
#> intercept V1 V2 V3 V4 V5
#> -0.009687042 1.240319880 0.000000000 0.000000000 0.000000000 0.000000000
#> V6 V7 V8 V9 V10 V11
#> 0.883378583 0.000000000 0.000000000 0.000000000 0.725607300 0.000000000
#> V12 V13 V14 V15 V16 V17
#> 0.000000000 0.000000000 0.000000000 1.125958218 0.000000000 0.000000000
#> V18 V19 V20
#> 0.000000000 0.000000000 0.981544178
predict(fit, X = gau_data$X[1:5, ], kappa = cv.fit$kappa.min)
#> [1] 0.190596 2.228306 -1.425994 0.931749 -2.815322
plot(fit, xvar = "kappa", label = TRUE)
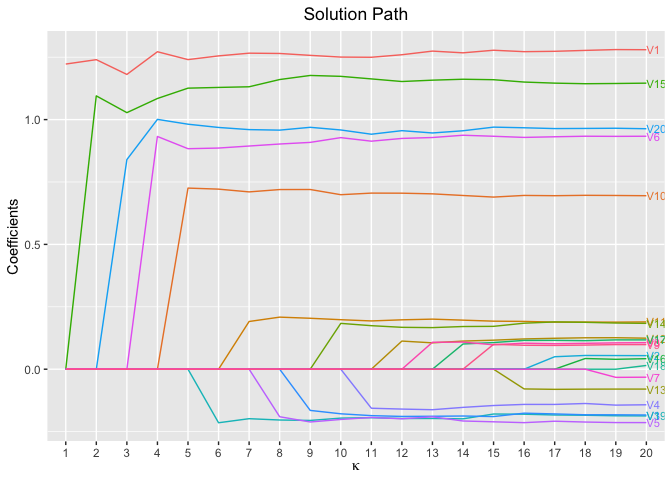
# Cross-Validation using L1 penalty
cv.fit <- cv.glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "l1", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V1 V4 V6 V10 V11
#> -0.03589837 1.09063811 -0.03020625 0.70163818 0.56874685 0.04658280
#> V14 V15 V19 V20
#> 0.01969490 0.96583003 -0.06633302 0.81279715
plot(cv.fit)
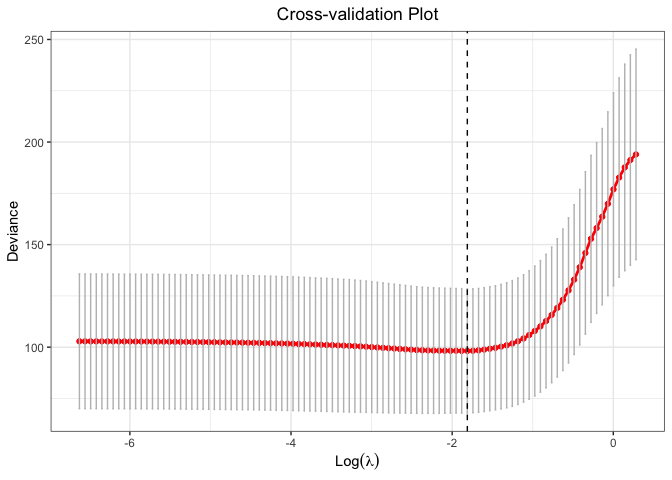
# Single Model Fit using L1 penalty
fit <- glmtlp(gau_data$X, gau_data$y, family = "gaussian", penalty = "l1")
coef(fit, lambda = cv.fit$lambda.min)
#> intercept V1 V2 V3 V4 V5
#> -0.03589837 1.09063811 0.00000000 0.00000000 -0.03020625 0.00000000
#> V6 V7 V8 V9 V10 V11
#> 0.70163818 0.00000000 0.00000000 0.00000000 0.56874685 0.04658280
#> V12 V13 V14 V15 V16 V17
#> 0.00000000 0.00000000 0.01969490 0.96583003 0.00000000 0.00000000
#> V18 V19 V20
#> 0.00000000 -0.06633302 0.81279715
predict(fit, X = gau_data$X[1:5, ], lambda = cv.fit$lambda.min)
#> [1] 0.03978789 1.83217872 -0.97812631 0.54083363 -2.01470751
plot(fit, xvar = "lambda", label = TRUE)
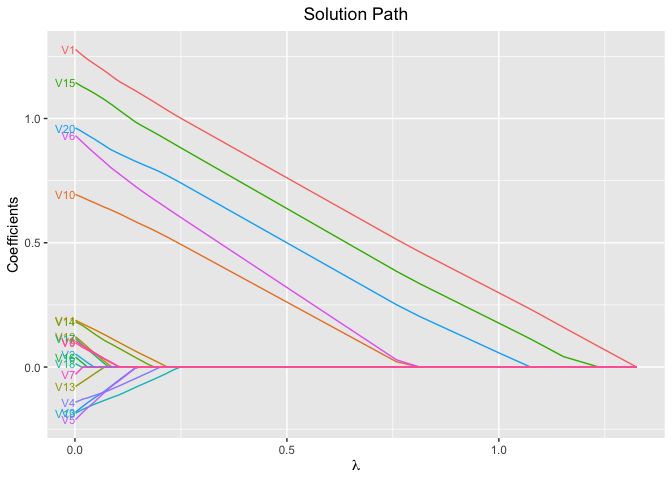
Examples for Logistic Regression Models
The following are three examples which show you how to use glmtlp to fit logistic regression models:
data("bin_data")
colnames(bin_data$X)[bin_data$beta != 0]
#> [1] "V1" "V6" "V10" "V15" "V20"
# Cross-Validation using L1 penalty
cv.fit <- cv.glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "tlp", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V6 V20
#> -0.1347141 0.8256183 0.9940325
plot(cv.fit)
#> Warning: Removed 98 row(s) containing missing values (geom_path).
#> Warning: Removed 98 rows containing missing values (geom_point).
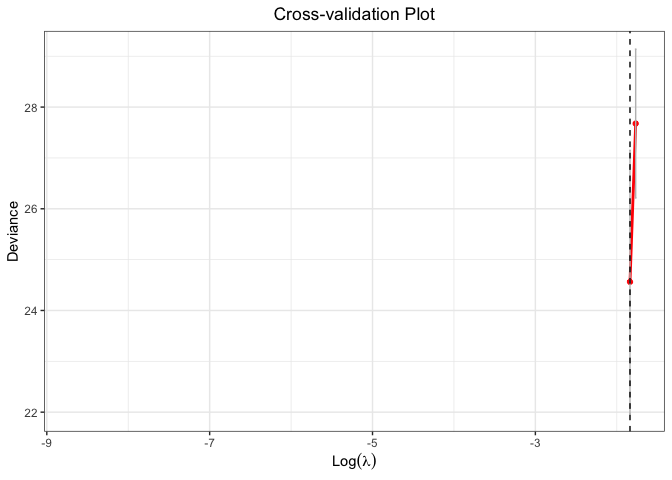
fit <- glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "tlp")
coef(fit, lambda = cv.fit$lambda.min)
#> intercept V1 V2 V3 V4 V5 V6
#> -0.1347141 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.8256183
#> V7 V8 V9 V10 V11 V12 V13
#> 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> V14 V15 V16 V17 V18 V19 V20
#> 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.9940325
predict(fit, X = bin_data$X[1:5, ], type = "response", lambda = cv.fit$lambda.min)
#> [1] 0.42562483 0.89838483 0.09767039 0.90898462 0.20822294
plot(fit, xvar = "log_lambda", label = TRUE)
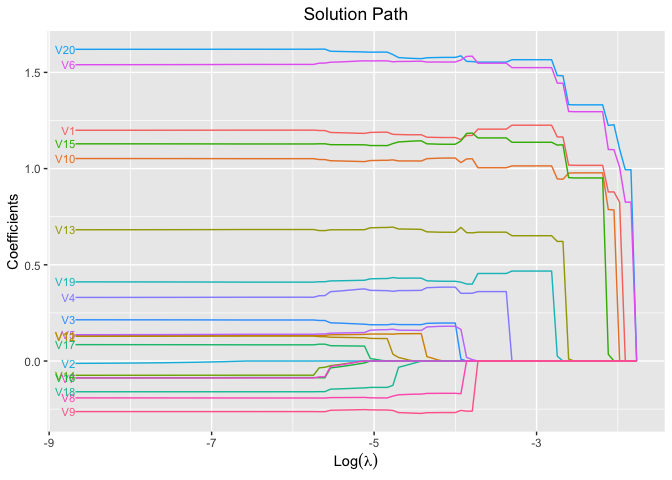
# Cross-Validation using L1 penalty
cv.fit <- cv.glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "l0", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V1 V6 V20
#> -0.07161141 0.82529133 1.00648111 1.10064640
plot(cv.fit)
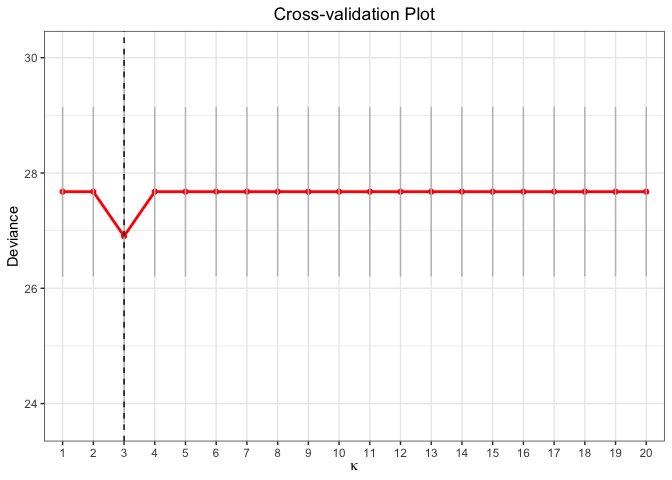
fit <- glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "l0")
coef(fit, kappa = cv.fit$kappa.min)
#> intercept V1 V2 V3 V4 V5
#> -0.07161141 0.82529133 0.00000000 0.00000000 0.00000000 0.00000000
#> V6 V7 V8 V9 V10 V11
#> 1.00648111 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> V12 V13 V14 V15 V16 V17
#> 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
#> V18 V19 V20
#> 0.00000000 0.00000000 1.10064640
predict(fit, X = bin_data$X[1:5, ], kappa = cv.fit$kappa.min)
#> [1] -0.2806496 2.9558219 -2.3128480 2.9849274 -0.9936015
plot(fit, xvar = "kappa", label = TRUE)
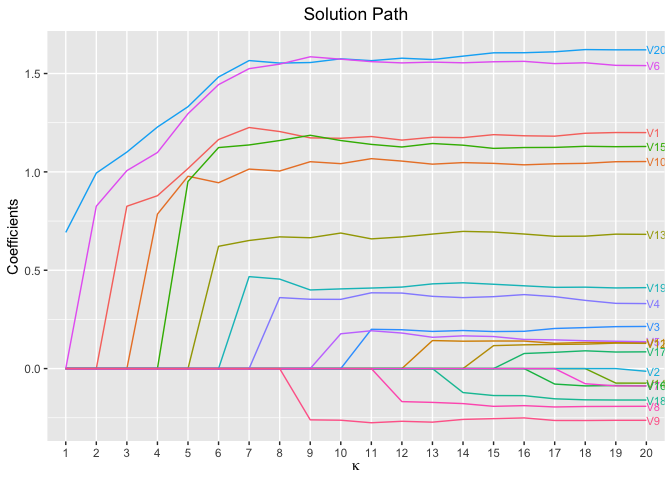
# Cross-Validation using L1 penalty
cv.fit <- cv.glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "l1", ncores=2)
coef(cv.fit)[abs(coef(cv.fit)) > 0]
#> intercept V1 V3 V4 V5 V6
#> -0.04593027 0.79539914 0.06262547 0.19102595 0.06793078 1.05865751
#> V8 V9 V10 V11 V13 V15
#> -0.06306159 -0.09101621 0.71050104 0.01838134 0.38267285 0.74771918
#> V19 V20
#> 0.26189535 1.08151085
plot(cv.fit)
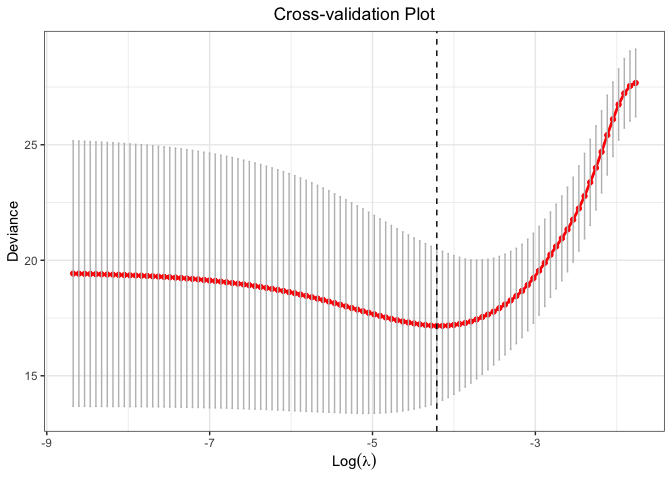
fit <- glmtlp(bin_data$X, bin_data$y, family = "binomial", penalty = "l1")
coef(fit, lambda = cv.fit$lambda.min)
#> intercept V1 V2 V3 V4 V5
#> -0.04593027 0.79539914 0.00000000 0.06262547 0.19102595 0.06793078
#> V6 V7 V8 V9 V10 V11
#> 1.05865751 0.00000000 -0.06306159 -0.09101621 0.71050104 0.01838134
#> V12 V13 V14 V15 V16 V17
#> 0.00000000 0.38267285 0.00000000 0.74771918 0.00000000 0.00000000
#> V18 V19 V20
#> 0.00000000 0.26189535 1.08151085
predict(fit, X = bin_data$X[1:5, ], type = "response", lambda = cv.fit$lambda.min)
#> [1] 0.32934063 0.91919949 0.02726264 0.94908173 0.02600642
plot(fit, xvar = "lambda", label = TRUE)
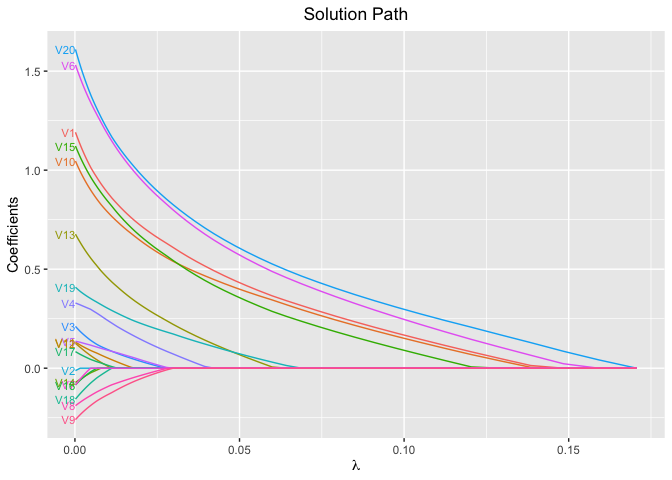
References
Shen, X., Pan, W., & Zhu, Y. (2012). Likelihood-based selection and sharp parameter estimation. Journal of the American Statistical Association, 107(497), 223-232. https://doi.org/10.1080/01621459.2011.645783.
Shen, X., Pan, W., Zhu, Y., & Zhou, H. (2013). On constrained and regularized high-dimensional regression. Annals of the Institute of Statistical Mathematics, 65(5), 807-832. https://doi.org/10.1007/s10463-012-0396-3
Li, C., Shen, X., & Pan, W. (2021). Inference for a Large Directed Graphical Model with Interventions. arXiv preprint arXiv:2110.03805. https://arxiv.org/abs/2110.03805
Tibshirani, R., Bien, J., Friedman, J., Hastie, T., Simon, N., Taylor, J., & Tibshirani, R. J. (2012). Strong rules for discarding predictors in lasso‐type problems. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 74(2), 245-266. https://doi.org/10.1111/j.1467-9868.2011.01004.x.
Yang, Yi, and Hui Zou. “A coordinate majorization descent algorithm for l1 penalized learning.” Journal of Statistical Computation and Simulation 84.1 (2014): 84-95. https://doi.org/10.1080/00949655.2012.695374.