Hierarchical Joint Analysis of Marginal Summary Statistics.

hJAM

hJAM is a hierarchical model which unifies the framework of Mendelian Randomization and Transcriptome-wide association studies.

Installation

You can install the development version from GitHub with:

if (!require("devtools")) { install.packages("devtools") } else {}
devtools::install_github("lailylajiang/hJAM")

Example

This is a basic example of fitting hJAM model:

library(hJAM)
# Download the data for data example 2 from the package
data(Gl)
data(betas.Gy)
data(marginal_A)

If you don't have conditional A matrix, you can use get_cond_A (if more than one X) or get_cond_alpha (if only one X) to convert the marginal effects to conditional A matrix with the reference panel.

conditional_A = get_cond_A(marginal_A = marginal_A, Gl = Gl, N.Gx = 339224, ridgeTerm = T)
conditional_alpha = get_cond_alpha(alphas = marginal_A[, 1], Gl = Gl, N.Gx = 339224, ridgeTerm = T)

After obtained the conditional A matrix, fit hJAM model with function hJAM_lnreg.

# fit the hJAM model
hJAM_lnreg(betas.Gy = betas.Gy, Gl = Gl, N.Gy = 459324, A = conditional_A, ridgeTerm = T)
#> ------------------------------------------------------ 
#>                    hJAM output                         
#> ------------------------------------------------------ 
#> Number of SNPs used in model: 210 
#> 
#>     Estimate StdErr         95% CI       Pvalue
#> bmi    0.322  0.061 (0.202, 0.442) 3.189944e-07
#> t2d    0.119  0.017 (0.085, 0.153) 4.124526e-11
#> ------------------------------------------------------

In the package, you could also implement hJAM with Egger regression, which is designed to detect the unmeasured pleiotropy effect. The function for hJAM with Egger regression is hJAM_egger.

# fit the hJAM model
hJAM_egger(betas.Gy = betas.Gy, Gl = Gl, N.Gy = 459324, A = conditional_A, ridgeTerm = T)
#> ------------------------------------------------------ 
#>                    hJAM egger output                   
#> ------------------------------------------------------ 
#> Number of SNPs used in model: 210 
#> 
#>     Estimate StdErr        95% CI       Pvalue
#> bmi    0.302  0.070 (0.163, 0.44) 2.817908e-05
#> t2d    0.107  0.027 (0.055, 0.16) 8.175202e-05
#> 
#> Intercept
#>      Est.Int StdErr.Int 95% CI.Int        Pvalue.Int
#> [1,] "0.453" "0.787"    "(-1.099, 2.005)" "0.565"   
#> ------------------------------------------------------

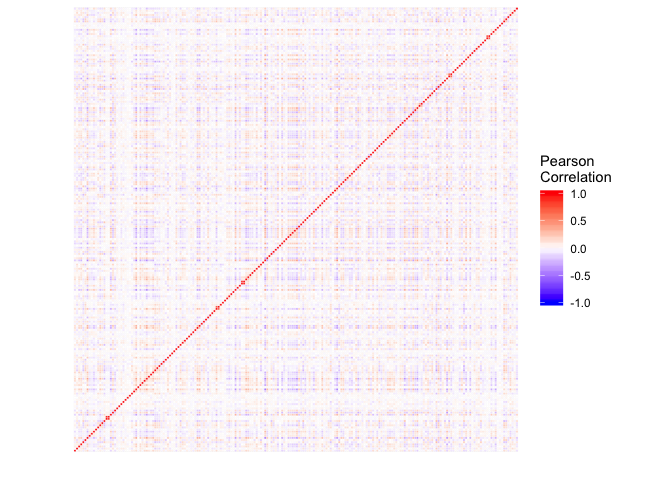
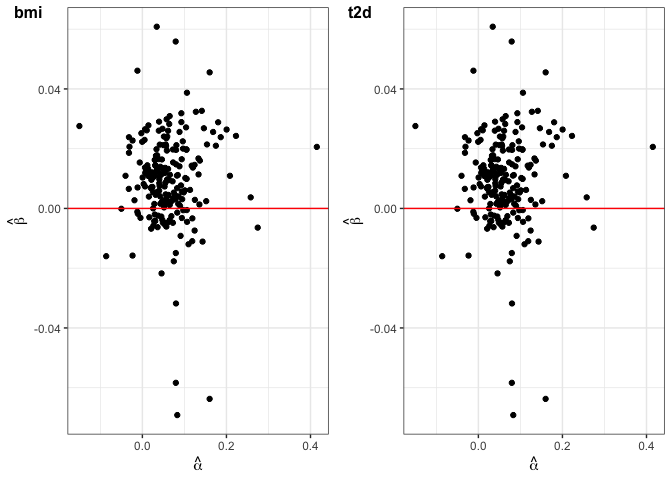
The user could use SNPs_heatmap and SNPs_scatter_plot to display the correlation and pattern of the SNPs that the user used in the analysis.

scatter_plot_p = SNPs_scatter_plot(A = conditional_A, betas.Gy = betas.Gy, num_X = 2)
scatter_plot_p

heatmap_p = SNPs_heatmap(Gl)
heatmap_p