Description
Unidimensional Item Response Theory Modeling.
Description
Fit unidimensional item response theory (IRT) models to a mixture of dichotomous and polytomous data, calibrate online item parameters (i.e., pretest and operational items), estimate examinees' abilities, and examine the IRT model-data fit on item-level in different ways as well as provide useful functions related to IRT analyses such as IRT model-data fit evaluation and differential item functioning analysis. The bring.flexmirt() and write.flexmirt() functions were written by modifying the read.flexmirt() function (Pritikin & Falk (2022) <doi:10.1177/0146621620929431>). The bring.bilog() and bring.parscale() functions were written by modifying the read.bilog() and read.parscale() functions, respectively (Weeks (2010) <doi:10.18637/jss.v035.i12>). The bisection() function was written by modifying the bisection() function (Howard (2017, ISBN:9780367657918)). The code of the inverse test characteristic curve scoring in the est_score() function was written by modifying the irt.eq.tse() function (González (2014) <doi:10.18637/jss.v059.i07>). In est_score() function, the code of weighted likelihood estimation method was written by referring to the Pi(), Ji(), and Ii() functions of the catR package (Magis & Barrada (2017) <doi:10.18637/jss.v076.c01>).
README.md
irtQ
The goal of irtQ is to fit unidimensional item response theory (IRT) models to mixture of dichotomous and polytomous data, calibrate online item parameters (i.e., pretest and operational items), estimate examinees abilities, and examine the IRT model-data fit on item-level in different ways as well as provide useful functions related to IRT analyses.
For the item parameter estimation, the marginal maximum likelihood estimation with expectation-maximization (MMLE-EM) algorithm (Bock & Aitkin, 1981) is used. For the online calibration, the fixed item parameter calibration (FIPC) method (e.g., Kim, 2006) and the fixed ability parameter calibration (FAPC) method (Ban, Hanson, Wang, Yi, & Harris, 2001; stocking, 1988), often called Stocking’s Method A, are provided. For the ability estimation, several popular scoring methods (e.g., MLE, EAP, and MAP) are implemented. In terms of assessing the IRT model-data fit, one of distinguished features of this package is that it gives not only item fit statistics (e.g., chi-square fit statistic (X2; e.g., Bock, 1960; Yen, 1981), likelihood ratio chi-square fit statistic (G2; McKinley & Mills, 1985), infit and outfit statistics (Ames et al., 2015), and S-X2 (Orlando & Thissen, 2000, 2003)) but also graphical displays to look at residuals between the observed data and model-based predictions (Hambleton, Swaminathan, & Rogers, 1991).
In addition, there are many useful functions such as analyzing differential item functioning (DIF), computing asymptotic variance-covariance matrices of item parameter estimates, importing item and/or ability parameters from popular IRT software, running flexMIRT (Cai, 2017) through R, generating simulated data, computing the conditional distribution of observed scores using the Lord-Wingersky recursion formula, computing item and test information functions, computing item and test characteristic curve functions, and plotting item and test characteristic curves and item and test information functions.
Installation
You can install the released version of irtplay from CRAN with:
install.packages("irtQ")
1. Online item calibration with the fixed item parameter calibration (FIPC) method (e.g., Kim, 2006)
The fixed item parameter calibration (FIPC) is one of useful online item calibration methods for computerized adaptive testing (CAT) to put the parameter estimates of pretest items on the same scale of operational item parameter estimates without post hoc linking/scaling (Ban, Hanson, Wang, Yi, & Harris, 2001; Chen & Wang, 2016). In FIPC, the operational item parameters are fixed to estimate the characteristic of the underlying latent variable prior distribution when calibrating the pretest items. More specifically, the underlying latent variable prior distribution of the operational items is estimated during the calibration of the pretest items to put the item parameters of the pretest items on the scale of the operational item parameters (Kim, 2006). In irtQ package, FIPC is implemented with two main steps:
- Prepare a response data set and the item metadata of the fixed (or operational) items.
- Implement FIPC to estimate the item parameters of pretest items using the
est_irt()function.
(1) Preparing a data set
To run the est_irt() function, it requires two data sets:
- Item metadata set (i.e., model, score category, and item parameters. see the desciption of the argument
xin the functionest_irt). - Examinees’ response data set for the items. It should be a matrix format where a row and column indicate the examinees and the items, respectively. The order of the columns in the response data set must be exactly the same as the order of rows of the item metadata.
(2) Estimating the pretest item parameters
When FIPC is implemented in est_irt() function, the pretest item parameters are estimated by fixing the operational item parameters. To estimate the item parameters, you need to provide the item metadata in the argument x and the response data in the argument data.
It is worthwhile to explain about how to prepare the item metadata set in the argument x. A specific form of a data frame should be used for the argument x. The first column should have item IDs, the second column should contain the number of score categories of the items, and the third column should include IRT models. The available IRT models are “1PLM”, “2PLM”, “3PLM”, and “DRM” for dichotomous items, and “GRM” and “GPCM” for polytomous items. Note that “DRM” covers all dichotomous IRT models (i.e, “1PLM”, “2PLM”, and “3PLM”) and “GRM” and “GPCM” represent the graded response model and (generalized) partial credit model, respectively. From the fourth column, item parameters should be included. For dichotomous items, the fourth, fifth, and sixth columns represent the item discrimination (or slope), item difficulty, and item guessing parameters, respectively. When “1PLM” or “2PLM” is specified for any items in the third column, NAs should be inserted for the item guessing parameters. For polytomous items, the item discrimination (or slope) parameters should be contained in the fourth column and the item threshold (or step) parameters should be included from the fifth to the last columns. When the number of categories differs between items, the empty cells of item parameters should be filled with NAs. See est_irt for more details about the item metadata.
Also, you should specify in the argument fipc = TRUE and a specific FIPC method in the argument fipc.method. Finally, you should provide a vector of the location of the items to be fixed in the argument fix.loc. For more details about implementing FIPC, see the description of the est_irt() function.
When implementing FIPC, you can estimate both the emprical histogram and the scale of latent variable prior distribution by setting EmpHist = TRUE. If EmpHist = FALSE, the normal prior distribution is used during the item parameter estimation and the scale of the normal prior distribution is updated during the EM cycle.
If necessary, you need to specify whether prior distributions of item slope and guessing parameters (only for the IRT 3PL model) are used in the arguments of use.aprior and use.gprior, respectively. If you decide to use the prior distributions, you should specify what distributions will be used for the prior distributions in the arguments of aprior and gprior, respectively. Currently three probability distributions of Beta, Log-normal, and Normal distributions are available.
In addition, if the response data include missing values, you must indicate the missing value in argument missing.
Once the est_irt() function has been implemented, you’ll get a list of several internal objects such as the item parameter estimates, standard error of the parameter estimates.
2. Online item calibration with the fixed ability parameter calibration method (e.g., Stocking, 1988)
In CAT, the fixed ability parameter calibration (FAPC), often called Stocking’s Method A, is the relatively simplest and most straightforward online calibration method, which is the maximum likelihood estimation of the item parameters given the proficiency estimates. In CAT, FAPC can be used to put the parameter estimates of pretest items on the same scale of operational item parameter estimates and recalibrate the operational items to evaluate the parameter drifts of the operational items (Chen & Wang, 2016; Stocking, 1988). Also, FAPC is known to result in accurate, unbiased item parameters calibration when items are randomly rather than adaptively administered to examinees, which occurs most commonly with pretest items (Ban et al., 2001; Chen & Wang, 2016). Using irtQ package, the FAPC is implemented to calibrate the items with two main steps:
- Prepare a data set for the calibration of item parameters (i.e., item response data and ability estimates).
- Implement the FAPC to estimate the item parameters using the
est_item()function.
(1) Preparing a data set
To run the est_item() function, it requires two data sets:
- Examinees’ ability (or proficiency) estimates. It should be in the format of a numeric vector.
- Examinees’ response data set for the items. It should be in the format of matrix where a row and column indicate the examinees and the items, respectively. The order of the examinees in the response data set must be exactly the same as that of the examinees’ ability estimates.
(2) Estimating the pretest item parameters
The est_item() function estimates the pretest item parameters given the proficiency estimates. To estimate the item parameters, you need to provide the response data in the argument data and the ability estimates in the argument score.
Also, you should provide a string vector of the IRT models in the argument model to indicate what IRT model is used to calibrate each item. Available IRT models are “1PLM”, “2PLM”, “3PLM”, and “DRM” for dichotomous items, and “GRM” and “GPCM” for polytomous items. “GRM” and “GPCM” represent the graded response model and (generalized) partial credit model, respectively. Note that “DRM” is considered as “3PLM” in this function. If a single character of the IRT model is specified, that model will be recycled across all items.
The est_item() function requires a vector of the number of score categories for the items in the argument cats. For example, a dichotomous item has two score categories. If a single numeric value is specified, that value will be recycled across all items. If NULL and all items are binary items (i.e., dichotomous items), it assumes that all items have two score categories.
If necessary, you need to specify whether prior distributions of item slope and guessing parameters (only for the IRT 3PL model) are used in the arguments of use.aprior and use.gprior, respectively. If you decide to use the prior distributions, you should specify what distributions will be used for the prior distributions in the arguments of aprior and gprior, respectively. Currently three probability distributions of Beta, Log-normal, and Normal distributions are available.
In addition, if the response data include missing values, you must indicate the missing value in argument missing.
Once the est_item function has been implemented, you’ll get a list of several internal objects such as the item parameter estimates, standard error of the parameter estimates.
3. The process of evaluating the IRT model-data fit
One way to assess goodness of IRT model-data fit is through an item fit analysis by examining the traditional item fit statistics and looking at the discrepancy between the observed data and model-based predictions. Using irtQ package, the traditional approach of evaluating the IRT model-data fit on item-level can be implemented with three main steps:
- Prepare a data set for the IRT item fit analysis (i.e., item metadata, ability estimates, and response data).
- Obtain the IRT fit statistics such as the X2, G2, infit, and outfit statistics using the
irtfit()function. - Based on the results of IRT model fit analysis (i.e., an object of class
irtfit) obtained in step 2, draw the IRT residual plots (i.e., raw residual and standardized residual plots) usingplotmethod.
(1) Preparing a data set
Before conducting the IRT model fit analysis, it is necessary to prepare a data set. To run the irtfit() function, it requires three data sets:
- Item metadata including the item ID, number of score categories, IRT models, and item parameters. The item metadata should be in the format of data frame. You can prepare the data either by using the
shape_df()function or by creating a data frame of the item metadata by yourself. If you have output files of item parameter estimates obtained from one of the IRT software such as BILOG-MG 3, PARSCALE 4, flexMIRT, and mirt (R package), the item metadata can be easily obtained using the functions ofbring.bilog(),bring.parscale(),bring.flexmirt(),bring.mirt(). See the functions ofirtfit(),test.info(), orsimdat()for more details about the item metadata format. - Examinees’ ability (or proficiency) estimates. It should be in the format of a numeric vector.
- Examinees’ response data set for the items. It should be in the format of matrix where a row and column indicate the examinees and the items, respectively. The order of the examinees in the response data set must be exactly the same as that of the examinees’ ability estimates. The order of the items in the response data set must be exactly the same as that of the items in the item metadata.
(2) Computing the IRT model-data fit statistics
The irtfit() function computes the traditional IRT item fit statistics such as X2, G2, infit, and outfit statistics. To calculate the X2 and G2 statistics, two methods are available to divide the ability scale into several groups. The two methods are “equal.width” for dividing the scale by an equal length of the interval and “equal.freq” for dividing the scale by an equal frequency of examinees. Also, you need to specify the location of ability point at each group (or interval) where the expected probabilities of score categories are calculated from the IRT models. Available locations are “average” for computing the expected probability at the average point of examinees’ ability estimates in each group and “middle” for computing the expected probability at the midpoint of each group.
To use the irtfit() function, you need to insert the item metadata in the argument x, the ability estimates in the argument score, and the response data in the argument data. If you want to divide the ability scale into other than ten groups, you need to specify the number of groups in the argument n.width. In addition, if the response data include missing values, you must indicate the missing value in argument missing.
Once the irtfit() function has been implemented, you’ll get the fit statistic results and the contingency tables for every item used to calculate the X2 and G2 fit statistics.
(3) Drawing the IRT residual plots
Using the saved object of class irtfit, you can use the plot method to evaluate the IRT raw residual and standardized residual plots.
Because the plot method can draw the residual plots for an item at a time, you have to indicate which item will be examined. For this, you can specify an integer value, which is the location of the studied item, in the argument item.loc.
In terms of the raw residual plot, the argument ci.method is used to select a method to estimate the confidence intervals among four methods. Those methods are “wald” for the Wald interval, which is based on the normal approximation (Laplace, 1812), “cp” for Clopper-Pearson interval (Clopper & Pearson, 1934), “wilson” for Wilson score interval (Wilson, 1927), and “wilson.cr” for Wilson score interval with continuity correction (Newcombe, 1998).
3. Examples of implementing online calibration and evaluating the IRT model-data fit
library("irtQ")
##----------------------------------------------------------------------------
# 1. The example code below shows how to prepare
# the data sets and how to implement the fixed
# item parameter calibration (FIPC):
##----------------------------------------------------------------------------
## Step 1: prepare a data set In this example, we
## generated examinees' true proficiency
## parameters and simulated the item response
## data using the function 'simdat'.
## import the '-prm.txt' output file from
## flexMIRT
flex_sam <- system.file("extdata", "flexmirt_sample-prm.txt",
package = "irtQ")
# select the item metadata
x <- bring.flexmirt(file = flex_sam, "par")$Group1$full_df
# generate 1,000 examinees' latent abilities from
# N(0.4, 1.3)
set.seed(20)
score <- rnorm(1000, mean = 0.4, sd = 1.3)
# simulate the response data
sim.dat <- simdat(x = x, theta = score, D = 1)
## Step 2: Estimate the item parameters fit the
## 3PL model to all dichotmous items, fit the GRM
## model to all polytomous data, fix the five 3PL
## items (1st - 5th items) and three GRM items
## (53th to 55th items) also, estimate the
## empirical histogram of latent variable
fix.loc <- c(1:5, 53:55)
(mod.fix1 <- est_irt(x = x, data = sim.dat, D = 1,
use.gprior = TRUE, gprior = list(dist = "beta",
params = c(5, 16)), EmpHist = TRUE, Etol = 0.001,
fipc = TRUE, fipc.method = "MEM", fix.loc = fix.loc,
verbose = FALSE))
#>
#> Call:
#> est_irt(x = x, data = sim.dat, D = 1, use.gprior = TRUE, gprior = list(dist = "beta",
#> params = c(5, 16)), EmpHist = TRUE, Etol = 0.001, fipc = TRUE,
#> fipc.method = "MEM", fix.loc = fix.loc, verbose = FALSE)
#>
#> Item parameter estimation using MMLE-EM.
#> 36 E-step cycles were completed using 49 quadrature points.
#> First-order test: Convergence criteria are satisfied.
#> Second-order test: Solution is a possible local maximum.
#> Computation of variance-covariance matrix:
#> Variance-covariance matrix of item parameter estimates is obtainable.
#>
#> Log-likelihood: -31049.92
summary(mod.fix1)
#>
#> Call:
#> est_irt(x = x, data = sim.dat, D = 1, use.gprior = TRUE, gprior = list(dist = "beta",
#> params = c(5, 16)), EmpHist = TRUE, Etol = 0.001, fipc = TRUE,
#> fipc.method = "MEM", fix.loc = fix.loc, verbose = FALSE)
#>
#> Summary of the Data
#> Number of Items: 55
#> Number of Cases: 1000
#>
#> Summary of Estimation Process
#> Maximum number of EM cycles: 500
#> Convergence criterion of E-step: 0.001
#> Number of rectangular quadrature points: 49
#> Minimum & Maximum quadrature points: -6, 6
#> Number of free parameters: 147
#> Number of fixed items: 8
#> Number of E-step cycles completed: 36
#> Maximum parameter change: 0.0009203792
#>
#> Processing time (in seconds)
#> EM algorithm: 4.73
#> Standard error computation: 2.65
#> Total computation: 7.89
#>
#> Convergence and Stability of Solution
#> First-order test: Convergence criteria are satisfied.
#> Second-order test: Solution is a possible local maximum.
#> Computation of variance-covariance matrix:
#> Variance-covariance matrix of item parameter estimates is obtainable.
#>
#> Summary of Estimation Results
#> -2loglikelihood: 62099.84
#> Akaike Information Criterion (AIC): 62393.84
#> Bayesian Information Criterion (BIC): 63115.28
#> Item Parameters:
#> id cats model par.1 se.1 par.2 se.2 par.3 se.3 par.4 se.4
#> 1 CMC1 2 3PLM 0.76 NA 1.46 NA 0.26 NA NA NA
#> 2 CMC2 2 3PLM 1.92 NA -1.05 NA 0.18 NA NA NA
#> 3 CMC3 2 3PLM 0.93 NA 0.39 NA 0.10 NA NA NA
#> 4 CMC4 2 3PLM 1.05 NA -0.41 NA 0.20 NA NA NA
#> 5 CMC5 2 3PLM 0.87 NA -0.12 NA 0.16 NA NA NA
#> 6 CMC6 2 3PLM 1.47 0.15 0.61 0.09 0.07 0.03 NA NA
#> 7 CMC7 2 3PLM 1.45 0.25 1.23 0.14 0.24 0.04 NA NA
#> 8 CMC8 2 3PLM 0.80 0.11 0.82 0.21 0.12 0.05 NA NA
#> 9 CMC9 2 3PLM 0.81 0.13 0.63 0.28 0.20 0.07 NA NA
#> 10 CMC10 2 3PLM 1.55 0.21 0.16 0.14 0.18 0.05 NA NA
#> 11 CMC11 2 3PLM 0.99 0.17 -0.01 0.33 0.32 0.08 NA NA
#> 12 CMC12 2 3PLM 0.86 0.13 1.30 0.18 0.11 0.04 NA NA
#> 13 CMC13 2 3PLM 1.48 0.26 1.61 0.12 0.18 0.03 NA NA
#> 14 CMC14 2 3PLM 1.53 0.21 0.25 0.16 0.27 0.05 NA NA
#> 15 CMC15 2 3PLM 1.53 0.18 -0.11 0.13 0.14 0.05 NA NA
#> 16 CMC16 2 3PLM 2.16 0.22 0.02 0.07 0.08 0.03 NA NA
#> 17 CMC17 2 3PLM 1.39 0.19 0.03 0.17 0.20 0.06 NA NA
#> 18 CMC18 2 3PLM 1.36 0.27 1.34 0.16 0.27 0.04 NA NA
#> 19 CMC19 2 3PLM 2.48 0.37 -0.94 0.12 0.19 0.06 NA NA
#> 20 CMC20 2 3PLM 1.80 0.37 -1.21 0.26 0.40 0.10 NA NA
#> 21 CMC21 2 3PLM 1.76 0.22 -0.98 0.17 0.21 0.07 NA NA
#> 22 CMC22 2 3PLM 0.94 0.13 -0.51 0.27 0.19 0.08 NA NA
#> 23 CMC23 2 3PLM 0.83 0.10 -0.37 0.23 0.13 0.06 NA NA
#> 24 CMC24 2 3PLM 0.98 0.21 1.86 0.20 0.22 0.04 NA NA
#> 25 CMC25 2 3PLM 0.63 0.09 -2.01 0.47 0.21 0.09 NA NA
#> 26 CMC26 2 3PLM 1.13 0.14 -1.68 0.28 0.22 0.09 NA NA
#> 27 CMC27 2 3PLM 1.19 0.14 0.01 0.16 0.14 0.05 NA NA
#> 28 CMC28 2 3PLM 2.23 0.26 -0.13 0.09 0.15 0.04 NA NA
#> 29 CMC29 2 3PLM 1.31 0.16 -1.32 0.22 0.19 0.08 NA NA
#> 30 CMC30 2 3PLM 1.63 0.30 1.03 0.15 0.37 0.04 NA NA
#> 31 CMC31 2 3PLM 1.03 0.15 0.93 0.17 0.15 0.05 NA NA
#> 32 CMC32 2 3PLM 1.55 0.21 -0.75 0.20 0.26 0.08 NA NA
#> 33 CMC33 2 3PLM 1.24 0.19 -1.09 0.30 0.31 0.10 NA NA
#> 34 CMC34 2 3PLM 1.34 0.16 0.31 0.15 0.17 0.05 NA NA
#> 35 CMC35 2 3PLM 1.24 0.15 -0.36 0.20 0.19 0.07 NA NA
#> 36 CMC36 2 3PLM 1.06 0.17 1.05 0.17 0.15 0.05 NA NA
#> 37 CMC37 2 3PLM 2.11 0.26 -0.29 0.11 0.16 0.05 NA NA
#> 38 CMC38 2 3PLM 0.57 0.11 -0.30 0.55 0.26 0.10 NA NA
#> 39 CFR1 5 GRM 2.09 0.13 -1.81 0.10 -1.14 0.07 -0.68 0.06
#> 40 CFR2 5 GRM 1.38 0.08 -0.70 0.08 -0.08 0.07 0.48 0.06
#> 41 AMC1 2 3PLM 1.25 0.18 0.62 0.16 0.18 0.05 NA NA
#> 42 AMC2 2 3PLM 1.79 0.22 -1.61 0.18 0.17 0.07 NA NA
#> 43 AMC3 2 3PLM 1.37 0.17 0.64 0.12 0.12 0.04 NA NA
#> 44 AMC4 2 3PLM 0.94 0.11 -0.22 0.23 0.16 0.06 NA NA
#> 45 AMC5 2 3PLM 1.11 0.33 2.83 0.26 0.21 0.03 NA NA
#> 46 AMC6 2 3PLM 2.22 0.37 1.70 0.09 0.19 0.02 NA NA
#> 47 AMC7 2 3PLM 1.16 0.13 0.02 0.14 0.10 0.04 NA NA
#> 48 AMC8 2 3PLM 1.31 0.16 0.33 0.15 0.18 0.05 NA NA
#> 49 AMC9 2 3PLM 1.22 0.13 0.30 0.12 0.09 0.04 NA NA
#> 50 AMC10 2 3PLM 1.83 0.28 1.48 0.09 0.15 0.03 NA NA
#> 51 AMC11 2 3PLM 1.68 0.22 -1.08 0.17 0.19 0.07 NA NA
#> 52 AMC12 2 3PLM 0.91 0.13 -0.82 0.35 0.26 0.09 NA NA
#> 53 AFR1 5 GRM 1.14 NA -0.37 NA 0.22 NA 0.85 NA
#> 54 AFR2 5 GRM 1.23 NA -2.08 NA -1.35 NA -0.71 NA
#> 55 AFR3 5 GRM 0.88 NA -0.76 NA -0.01 NA 0.67 NA
#> par.5 se.5
#> 1 NA NA
#> 2 NA NA
#> 3 NA NA
#> 4 NA NA
#> 5 NA NA
#> 6 NA NA
#> 7 NA NA
#> 8 NA NA
#> 9 NA NA
#> 10 NA NA
#> 11 NA NA
#> 12 NA NA
#> 13 NA NA
#> 14 NA NA
#> 15 NA NA
#> 16 NA NA
#> 17 NA NA
#> 18 NA NA
#> 19 NA NA
#> 20 NA NA
#> 21 NA NA
#> 22 NA NA
#> 23 NA NA
#> 24 NA NA
#> 25 NA NA
#> 26 NA NA
#> 27 NA NA
#> 28 NA NA
#> 29 NA NA
#> 30 NA NA
#> 31 NA NA
#> 32 NA NA
#> 33 NA NA
#> 34 NA NA
#> 35 NA NA
#> 36 NA NA
#> 37 NA NA
#> 38 NA NA
#> 39 -0.24 0.05
#> 40 1.05 0.07
#> 41 NA NA
#> 42 NA NA
#> 43 NA NA
#> 44 NA NA
#> 45 NA NA
#> 46 NA NA
#> 47 NA NA
#> 48 NA NA
#> 49 NA NA
#> 50 NA NA
#> 51 NA NA
#> 52 NA NA
#> 53 1.38 NA
#> 54 -0.12 NA
#> 55 1.25 NA
#> Group Parameters:
#> mu sigma2 sigma
#> estimates 0.40 1.88 1.37
#> se 0.04 0.08 0.03
# plot the estimated empirical histogram of
# latent variable prior distribution
(emphist <- getirt(mod.fix1, what = "weights"))
#> theta weight
#> 1 -6.00 2.301252e-10
#> 2 -5.75 1.434596e-09
#> 3 -5.50 8.649282e-09
#> 4 -5.25 5.019868e-08
#> 5 -5.00 2.782912e-07
#> 6 -4.75 1.456751e-06
#> 7 -4.50 7.085630e-06
#> 8 -4.25 3.134808e-05
#> 9 -4.00 1.227012e-04
#> 10 -3.75 4.100603e-04
#> 11 -3.50 1.119742e-03
#> 12 -3.25 2.386354e-03
#> 13 -3.00 3.889322e-03
#> 14 -2.75 5.167720e-03
#> 15 -2.50 6.767224e-03
#> 16 -2.25 1.053445e-02
#> 17 -2.00 1.742567e-02
#> 18 -1.75 2.236173e-02
#> 19 -1.50 2.498735e-02
#> 20 -1.25 3.374293e-02
#> 21 -1.00 4.224442e-02
#> 22 -0.75 4.948939e-02
#> 23 -0.50 7.710828e-02
#> 24 -0.25 8.024288e-02
#> 25 0.00 4.752956e-02
#> 26 0.25 5.636581e-02
#> 27 0.50 8.674316e-02
#> 28 0.75 6.936382e-02
#> 29 1.00 6.035964e-02
#> 30 1.25 6.234864e-02
#> 31 1.50 5.768393e-02
#> 32 1.75 4.254008e-02
#> 33 2.00 3.148380e-02
#> 34 2.25 3.111071e-02
#> 35 2.50 2.935626e-02
#> 36 2.75 1.950494e-02
#> 37 3.00 1.019680e-02
#> 38 3.25 5.154557e-03
#> 39 3.50 2.816466e-03
#> 40 3.75 1.753617e-03
#> 41 4.00 1.282170e-03
#> 42 4.25 1.097172e-03
#> 43 4.50 1.050444e-03
#> 44 4.75 1.046478e-03
#> 45 5.00 1.004637e-03
#> 46 5.25 8.721994e-04
#> 47 5.50 6.557355e-04
#> 48 5.75 4.168380e-04
#> 49 6.00 2.220842e-04
plot(emphist$weight ~ emphist$theta, xlab = "Theta",
ylab = "Density", type = "h")
##----------------------------------------------------------------------------
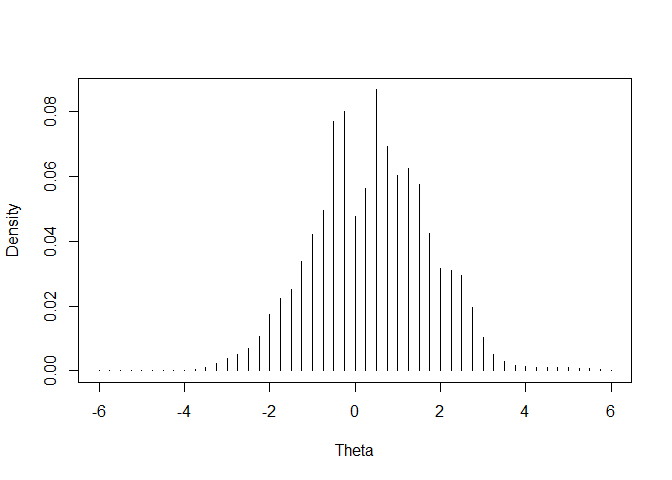
# 2. The example code below shows how to prepare
# the data sets and how to estimate the item
# parameters using the FAPC:
##----------------------------------------------------------------------------
## Step 1: prepare a data set In this example, we
## generated examinees' true proficiency
## parameters and simulated the item response
## data using the function 'simdat'. Because the
## true proficiency parameters are not known in
## reality, the true proficiencies would be
## replaced with the proficiency estimates for
## the calibration.
# import the '-prm.txt' output file from flexMIRT
flex_sam <- system.file("extdata", "flexmirt_sample-prm.txt",
package = "irtQ")
# select the item metadata
x <- bring.flexmirt(file = flex_sam, "par")$Group1$full_df
# modify the item metadata so that some items
# follow 1PLM, 2PLM and GPCM
x[c(1:3, 5), 3] <- "1PLM"
x[c(1:3, 5), 4] <- 1
x[c(1:3, 5), 6] <- 0
x[c(4, 8:12), 3] <- "2PLM"
x[c(4, 8:12), 6] <- 0
x[54:55, 3] <- "GPCM"
# generate examinees' abilities from N(0, 1)
set.seed(23)
score <- rnorm(500, mean = 0, sd = 1)
# simulate the response data
data <- simdat(x = x, theta = score, D = 1)
## Step 2: Estimate the item parameters 1) item
## parameter estimation: constrain the slope
## parameters of the 1PLM to be equal
(mod1 <- est_item(x, data, score, D = 1, fix.a.1pl = FALSE,
use.gprior = TRUE, gprior = list(dist = "beta",
params = c(5, 17)), use.startval = FALSE))
#> Starting...
#> Parsing input...
#> Estimating item parameters...
#> Estimation is finished.
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = FALSE,
#> use.gprior = TRUE, gprior = list(dist = "beta", params = c(5,
#> 17)), use.startval = FALSE)
#>
#> Fixed ability parameter calibration (Stocking's Method A).
#> All item parameters were successfully converged.
#>
#> Log-likelihood: -15830.66
summary(mod1)
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = FALSE,
#> use.gprior = TRUE, gprior = list(dist = "beta", params = c(5,
#> 17)), use.startval = FALSE)
#>
#> Summary of the Data
#> Number of Items in Response Data: 55
#> Number of Excluded Items: 0
#> Number of free parameters: 162
#> Number of Responses for Each Item:
#> id n
#> 1 CMC1 500
#> 2 CMC2 500
#> 3 CMC3 500
#> 4 CMC4 500
#> 5 CMC5 500
#> 6 CMC6 500
#> 7 CMC7 500
#> 8 CMC8 500
#> 9 CMC9 500
#> 10 CMC10 500
#> 11 CMC11 500
#> 12 CMC12 500
#> 13 CMC13 500
#> 14 CMC14 500
#> 15 CMC15 500
#> 16 CMC16 500
#> 17 CMC17 500
#> 18 CMC18 500
#> 19 CMC19 500
#> 20 CMC20 500
#> 21 CMC21 500
#> 22 CMC22 500
#> 23 CMC23 500
#> 24 CMC24 500
#> 25 CMC25 500
#> 26 CMC26 500
#> 27 CMC27 500
#> 28 CMC28 500
#> 29 CMC29 500
#> 30 CMC30 500
#> 31 CMC31 500
#> 32 CMC32 500
#> 33 CMC33 500
#> 34 CMC34 500
#> 35 CMC35 500
#> 36 CMC36 500
#> 37 CMC37 500
#> 38 CMC38 500
#> 39 CFR1 500
#> 40 CFR2 500
#> 41 AMC1 500
#> 42 AMC2 500
#> 43 AMC3 500
#> 44 AMC4 500
#> 45 AMC5 500
#> 46 AMC6 500
#> 47 AMC7 500
#> 48 AMC8 500
#> 49 AMC9 500
#> 50 AMC10 500
#> 51 AMC11 500
#> 52 AMC12 500
#> 53 AFR1 500
#> 54 AFR2 500
#> 55 AFR3 500
#>
#> Processing time (in seconds)
#> Total computation: 1.42
#>
#> Convergence of Solution
#> All item parameters were successfully converged.
#>
#> Summary of Estimation Results
#> -2loglikelihood: 31661.31
#> Item Parameters:
#> id cats model par.1 se.1 par.2 se.2 par.3 se.3 par.4 se.4
#> 1 CMC1 2 1PLM 1.02 0.06 1.60 0.13 NA NA NA NA
#> 2 CMC2 2 1PLM 1.02 NA -1.06 0.12 NA NA NA NA
#> 3 CMC3 2 1PLM 1.02 NA 0.40 0.10 NA NA NA NA
#> 4 CMC4 2 2PLM 1.02 NA -0.25 0.10 NA NA NA NA
#> 5 CMC5 2 1PLM 0.96 0.12 -0.43 0.11 NA NA NA NA
#> 6 CMC6 2 3PLM 1.88 0.27 0.67 0.09 0.10 0.03 NA NA
#> 7 CMC7 2 3PLM 0.88 0.17 1.03 0.23 0.13 0.05 NA NA
#> 8 CMC8 2 2PLM 0.92 0.12 0.87 0.13 NA NA NA NA
#> 9 CMC9 2 2PLM 1.00 0.12 0.89 0.13 NA NA NA NA
#> 10 CMC10 2 2PLM 1.61 0.15 0.09 0.07 NA NA NA NA
#> 11 CMC11 2 2PLM 1.07 0.12 -0.37 0.10 NA NA NA NA
#> 12 CMC12 2 2PLM 0.94 0.12 1.10 0.15 NA NA NA NA
#> 13 CMC13 2 3PLM 1.35 0.34 1.31 0.17 0.17 0.04 NA NA
#> 14 CMC14 2 3PLM 1.36 0.31 0.15 0.24 0.24 0.08 NA NA
#> 15 CMC15 2 3PLM 1.53 0.27 0.01 0.17 0.20 0.07 NA NA
#> 16 CMC16 2 3PLM 2.10 0.25 0.04 0.08 0.10 0.04 NA NA
#> 17 CMC17 2 3PLM 1.02 0.15 -0.41 0.22 0.16 0.07 NA NA
#> 18 CMC18 2 3PLM 1.27 0.38 1.42 0.20 0.22 0.05 NA NA
#> 19 CMC19 2 3PLM 2.25 0.32 -1.11 0.14 0.17 0.07 NA NA
#> 20 CMC20 2 3PLM 1.47 0.22 -1.74 0.22 0.18 0.08 NA NA
#> 21 CMC21 2 3PLM 1.38 0.21 -1.25 0.23 0.20 0.08 NA NA
#> 22 CMC22 2 3PLM 0.92 0.16 -0.55 0.28 0.19 0.08 NA NA
#> 23 CMC23 2 3PLM 1.10 0.22 -0.12 0.27 0.22 0.09 NA NA
#> 24 CMC24 2 3PLM 1.21 0.34 1.43 0.21 0.22 0.05 NA NA
#> 25 CMC25 2 3PLM 0.83 0.16 -1.51 0.40 0.21 0.09 NA NA
#> 26 CMC26 2 3PLM 1.07 0.18 -2.16 0.35 0.19 0.08 NA NA
#> 27 CMC27 2 3PLM 1.18 0.18 0.09 0.17 0.14 0.06 NA NA
#> 28 CMC28 2 3PLM 2.19 0.31 -0.17 0.11 0.19 0.05 NA NA
#> 29 CMC29 2 3PLM 2.48 0.54 -0.81 0.20 0.38 0.09 NA NA
#> 30 CMC30 2 3PLM 1.88 0.45 0.69 0.15 0.34 0.05 NA NA
#> 31 CMC31 2 3PLM 0.70 0.16 1.00 0.32 0.16 0.07 NA NA
#> 32 CMC32 2 3PLM 1.73 0.30 -0.78 0.21 0.26 0.09 NA NA
#> 33 CMC33 2 3PLM 1.07 0.17 -1.45 0.28 0.19 0.08 NA NA
#> 34 CMC34 2 3PLM 1.04 0.17 0.21 0.20 0.16 0.06 NA NA
#> 35 CMC35 2 3PLM 1.36 0.19 -0.45 0.17 0.16 0.06 NA NA
#> 36 CMC36 2 3PLM 0.88 0.17 0.97 0.23 0.14 0.05 NA NA
#> 37 CMC37 2 3PLM 2.13 0.26 -0.25 0.09 0.13 0.05 NA NA
#> 38 CMC38 2 3PLM 0.87 0.17 -0.31 0.32 0.20 0.09 NA NA
#> 39 CFR1 5 GRM 2.00 0.14 -1.88 0.12 -1.25 0.08 -0.70 0.06
#> 40 CFR2 5 GRM 1.39 0.11 -0.80 0.09 -0.13 0.07 0.60 0.08
#> 41 AMC1 2 3PLM 1.81 0.39 0.74 0.14 0.28 0.05 NA NA
#> 42 AMC2 2 3PLM 1.70 0.25 -1.59 0.20 0.19 0.08 NA NA
#> 43 AMC3 2 3PLM 1.30 0.25 0.68 0.16 0.16 0.05 NA NA
#> 44 AMC4 2 3PLM 0.94 0.17 -0.18 0.26 0.18 0.07 NA NA
#> 45 AMC5 2 3PLM 1.69 0.65 2.11 0.26 0.19 0.03 NA NA
#> 46 AMC6 2 3PLM 2.83 0.64 1.44 0.10 0.15 0.02 NA NA
#> 47 AMC7 2 3PLM 1.69 0.41 0.37 0.18 0.25 0.07 NA NA
#> 48 AMC8 2 3PLM 1.65 0.29 0.39 0.14 0.20 0.05 NA NA
#> 49 AMC9 2 3PLM 1.55 0.26 0.49 0.13 0.15 0.05 NA NA
#> 50 AMC10 2 3PLM 2.48 0.51 1.31 0.10 0.13 0.02 NA NA
#> 51 AMC11 2 3PLM 1.73 0.23 -1.02 0.15 0.16 0.07 NA NA
#> 52 AMC12 2 3PLM 0.95 0.20 -0.83 0.38 0.24 0.10 NA NA
#> 53 AFR1 5 GRM 1.14 0.10 -0.30 0.09 0.30 0.09 0.92 0.11
#> 54 AFR2 5 GPCM 1.33 0.11 -1.99 0.21 -1.31 0.15 -0.72 0.12
#> 55 AFR3 5 GPCM 0.89 0.07 -0.80 0.15 0.15 0.15 0.46 0.16
#> par.5 se.5
#> 1 NA NA
#> 2 NA NA
#> 3 NA NA
#> 4 NA NA
#> 5 NA NA
#> 6 NA NA
#> 7 NA NA
#> 8 NA NA
#> 9 NA NA
#> 10 NA NA
#> 11 NA NA
#> 12 NA NA
#> 13 NA NA
#> 14 NA NA
#> 15 NA NA
#> 16 NA NA
#> 17 NA NA
#> 18 NA NA
#> 19 NA NA
#> 20 NA NA
#> 21 NA NA
#> 22 NA NA
#> 23 NA NA
#> 24 NA NA
#> 25 NA NA
#> 26 NA NA
#> 27 NA NA
#> 28 NA NA
#> 29 NA NA
#> 30 NA NA
#> 31 NA NA
#> 32 NA NA
#> 33 NA NA
#> 34 NA NA
#> 35 NA NA
#> 36 NA NA
#> 37 NA NA
#> 38 NA NA
#> 39 -0.23 0.06
#> 40 1.09 0.10
#> 41 NA NA
#> 42 NA NA
#> 43 NA NA
#> 44 NA NA
#> 45 NA NA
#> 46 NA NA
#> 47 NA NA
#> 48 NA NA
#> 49 NA NA
#> 50 NA NA
#> 51 NA NA
#> 52 NA NA
#> 53 1.35 0.13
#> 54 -0.21 0.10
#> 55 1.35 0.19
#>
#> Group Parameters:
#> mu sigma
#> 0.03 1.02
# 2) item parameter estimation: fix the slope
# parameters of the 1PLM to 1
(mod2 <- est_item(x, data, score, D = 1, fix.a.1pl = TRUE,
a.val.1pl = 1, use.gprior = TRUE, gprior = list(dist = "beta",
params = c(5, 17)), use.startval = FALSE))
#> Starting...
#> Parsing input...
#> Estimating item parameters...
#> Estimation is finished.
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = TRUE,
#> a.val.1pl = 1, use.gprior = TRUE, gprior = list(dist = "beta",
#> params = c(5, 17)), use.startval = FALSE)
#>
#> Fixed ability parameter calibration (Stocking's Method A).
#> All item parameters were successfully converged.
#>
#> Log-likelihood: -15830.7
summary(mod2)
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = TRUE,
#> a.val.1pl = 1, use.gprior = TRUE, gprior = list(dist = "beta",
#> params = c(5, 17)), use.startval = FALSE)
#>
#> Summary of the Data
#> Number of Items in Response Data: 55
#> Number of Excluded Items: 0
#> Number of free parameters: 161
#> Number of Responses for Each Item:
#> id n
#> 1 CMC1 500
#> 2 CMC2 500
#> 3 CMC3 500
#> 4 CMC4 500
#> 5 CMC5 500
#> 6 CMC6 500
#> 7 CMC7 500
#> 8 CMC8 500
#> 9 CMC9 500
#> 10 CMC10 500
#> 11 CMC11 500
#> 12 CMC12 500
#> 13 CMC13 500
#> 14 CMC14 500
#> 15 CMC15 500
#> 16 CMC16 500
#> 17 CMC17 500
#> 18 CMC18 500
#> 19 CMC19 500
#> 20 CMC20 500
#> 21 CMC21 500
#> 22 CMC22 500
#> 23 CMC23 500
#> 24 CMC24 500
#> 25 CMC25 500
#> 26 CMC26 500
#> 27 CMC27 500
#> 28 CMC28 500
#> 29 CMC29 500
#> 30 CMC30 500
#> 31 CMC31 500
#> 32 CMC32 500
#> 33 CMC33 500
#> 34 CMC34 500
#> 35 CMC35 500
#> 36 CMC36 500
#> 37 CMC37 500
#> 38 CMC38 500
#> 39 CFR1 500
#> 40 CFR2 500
#> 41 AMC1 500
#> 42 AMC2 500
#> 43 AMC3 500
#> 44 AMC4 500
#> 45 AMC5 500
#> 46 AMC6 500
#> 47 AMC7 500
#> 48 AMC8 500
#> 49 AMC9 500
#> 50 AMC10 500
#> 51 AMC11 500
#> 52 AMC12 500
#> 53 AFR1 500
#> 54 AFR2 500
#> 55 AFR3 500
#>
#> Processing time (in seconds)
#> Total computation: 1.25
#>
#> Convergence of Solution
#> All item parameters were successfully converged.
#>
#> Summary of Estimation Results
#> -2loglikelihood: 31661.4
#> Item Parameters:
#> id cats model par.1 se.1 par.2 se.2 par.3 se.3 par.4 se.4
#> 1 CMC1 2 1PLM 1.00 NA 1.62 0.12 NA NA NA NA
#> 2 CMC2 2 1PLM 1.00 NA -1.08 0.11 NA NA NA NA
#> 3 CMC3 2 1PLM 1.00 NA 0.40 0.10 NA NA NA NA
#> 4 CMC4 2 2PLM 0.96 0.12 -0.43 0.11 NA NA NA NA
#> 5 CMC5 2 1PLM 1.00 NA -0.25 0.10 NA NA NA NA
#> 6 CMC6 2 3PLM 1.88 0.27 0.67 0.09 0.10 0.03 NA NA
#> 7 CMC7 2 3PLM 0.88 0.17 1.03 0.23 0.13 0.05 NA NA
#> 8 CMC8 2 2PLM 0.92 0.12 0.87 0.13 NA NA NA NA
#> 9 CMC9 2 2PLM 1.00 0.12 0.89 0.13 NA NA NA NA
#> 10 CMC10 2 2PLM 1.61 0.15 0.09 0.07 NA NA NA NA
#> 11 CMC11 2 2PLM 1.07 0.12 -0.37 0.10 NA NA NA NA
#> 12 CMC12 2 2PLM 0.94 0.12 1.10 0.15 NA NA NA NA
#> 13 CMC13 2 3PLM 1.35 0.34 1.31 0.17 0.17 0.04 NA NA
#> 14 CMC14 2 3PLM 1.36 0.31 0.15 0.24 0.24 0.08 NA NA
#> 15 CMC15 2 3PLM 1.53 0.27 0.01 0.17 0.20 0.07 NA NA
#> 16 CMC16 2 3PLM 2.10 0.25 0.04 0.08 0.10 0.04 NA NA
#> 17 CMC17 2 3PLM 1.02 0.15 -0.41 0.22 0.16 0.07 NA NA
#> 18 CMC18 2 3PLM 1.27 0.38 1.42 0.20 0.22 0.05 NA NA
#> 19 CMC19 2 3PLM 2.25 0.32 -1.11 0.14 0.17 0.07 NA NA
#> 20 CMC20 2 3PLM 1.47 0.22 -1.74 0.22 0.18 0.08 NA NA
#> 21 CMC21 2 3PLM 1.38 0.21 -1.25 0.23 0.20 0.08 NA NA
#> 22 CMC22 2 3PLM 0.92 0.16 -0.55 0.28 0.19 0.08 NA NA
#> 23 CMC23 2 3PLM 1.10 0.22 -0.12 0.27 0.22 0.09 NA NA
#> 24 CMC24 2 3PLM 1.21 0.34 1.43 0.21 0.22 0.05 NA NA
#> 25 CMC25 2 3PLM 0.83 0.16 -1.51 0.40 0.21 0.09 NA NA
#> 26 CMC26 2 3PLM 1.07 0.18 -2.16 0.35 0.19 0.08 NA NA
#> 27 CMC27 2 3PLM 1.18 0.18 0.09 0.17 0.14 0.06 NA NA
#> 28 CMC28 2 3PLM 2.19 0.31 -0.17 0.11 0.19 0.05 NA NA
#> 29 CMC29 2 3PLM 2.48 0.54 -0.81 0.20 0.38 0.09 NA NA
#> 30 CMC30 2 3PLM 1.88 0.45 0.69 0.15 0.34 0.05 NA NA
#> 31 CMC31 2 3PLM 0.70 0.16 1.00 0.32 0.16 0.07 NA NA
#> 32 CMC32 2 3PLM 1.73 0.30 -0.78 0.21 0.26 0.09 NA NA
#> 33 CMC33 2 3PLM 1.07 0.17 -1.45 0.28 0.19 0.08 NA NA
#> 34 CMC34 2 3PLM 1.04 0.17 0.21 0.20 0.16 0.06 NA NA
#> 35 CMC35 2 3PLM 1.36 0.19 -0.45 0.17 0.16 0.06 NA NA
#> 36 CMC36 2 3PLM 0.88 0.17 0.97 0.23 0.14 0.05 NA NA
#> 37 CMC37 2 3PLM 2.13 0.26 -0.25 0.09 0.13 0.05 NA NA
#> 38 CMC38 2 3PLM 0.87 0.17 -0.31 0.32 0.20 0.09 NA NA
#> 39 CFR1 5 GRM 2.00 0.14 -1.88 0.12 -1.25 0.08 -0.70 0.06
#> 40 CFR2 5 GRM 1.39 0.11 -0.80 0.09 -0.13 0.07 0.60 0.08
#> 41 AMC1 2 3PLM 1.81 0.39 0.74 0.14 0.28 0.05 NA NA
#> 42 AMC2 2 3PLM 1.70 0.25 -1.59 0.20 0.19 0.08 NA NA
#> 43 AMC3 2 3PLM 1.30 0.25 0.68 0.16 0.16 0.05 NA NA
#> 44 AMC4 2 3PLM 0.94 0.17 -0.18 0.26 0.18 0.07 NA NA
#> 45 AMC5 2 3PLM 1.69 0.65 2.11 0.26 0.19 0.03 NA NA
#> 46 AMC6 2 3PLM 2.83 0.64 1.44 0.10 0.15 0.02 NA NA
#> 47 AMC7 2 3PLM 1.69 0.41 0.37 0.18 0.25 0.07 NA NA
#> 48 AMC8 2 3PLM 1.65 0.29 0.39 0.14 0.20 0.05 NA NA
#> 49 AMC9 2 3PLM 1.55 0.26 0.49 0.13 0.15 0.05 NA NA
#> 50 AMC10 2 3PLM 2.48 0.51 1.31 0.10 0.13 0.02 NA NA
#> 51 AMC11 2 3PLM 1.73 0.23 -1.02 0.15 0.16 0.07 NA NA
#> 52 AMC12 2 3PLM 0.95 0.20 -0.83 0.38 0.24 0.10 NA NA
#> 53 AFR1 5 GRM 1.14 0.10 -0.30 0.09 0.30 0.09 0.92 0.11
#> 54 AFR2 5 GPCM 1.33 0.11 -1.99 0.21 -1.31 0.15 -0.72 0.12
#> 55 AFR3 5 GPCM 0.89 0.07 -0.80 0.15 0.15 0.15 0.46 0.16
#> par.5 se.5
#> 1 NA NA
#> 2 NA NA
#> 3 NA NA
#> 4 NA NA
#> 5 NA NA
#> 6 NA NA
#> 7 NA NA
#> 8 NA NA
#> 9 NA NA
#> 10 NA NA
#> 11 NA NA
#> 12 NA NA
#> 13 NA NA
#> 14 NA NA
#> 15 NA NA
#> 16 NA NA
#> 17 NA NA
#> 18 NA NA
#> 19 NA NA
#> 20 NA NA
#> 21 NA NA
#> 22 NA NA
#> 23 NA NA
#> 24 NA NA
#> 25 NA NA
#> 26 NA NA
#> 27 NA NA
#> 28 NA NA
#> 29 NA NA
#> 30 NA NA
#> 31 NA NA
#> 32 NA NA
#> 33 NA NA
#> 34 NA NA
#> 35 NA NA
#> 36 NA NA
#> 37 NA NA
#> 38 NA NA
#> 39 -0.23 0.06
#> 40 1.09 0.10
#> 41 NA NA
#> 42 NA NA
#> 43 NA NA
#> 44 NA NA
#> 45 NA NA
#> 46 NA NA
#> 47 NA NA
#> 48 NA NA
#> 49 NA NA
#> 50 NA NA
#> 51 NA NA
#> 52 NA NA
#> 53 1.35 0.13
#> 54 -0.21 0.10
#> 55 1.35 0.19
#>
#> Group Parameters:
#> mu sigma
#> 0.03 1.02
# 3) item parameter estimation: fix the guessing
# parameters of the 3PLM to 0.2
(mod3 <- est_item(x, data, score, D = 1, fix.a.1pl = TRUE,
fix.g = TRUE, a.val.1pl = 1, g.val = 0.2, use.startval = FALSE))
#> Starting...
#> Parsing input...
#> Estimating item parameters...
#> Estimation is finished.
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = TRUE,
#> fix.g = TRUE, a.val.1pl = 1, g.val = 0.2, use.startval = FALSE)
#>
#> Fixed ability parameter calibration (Stocking's Method A).
#> All item parameters were successfully converged.
#>
#> Log-likelihood: -15916.26
summary(mod3)
#>
#> Call:
#> est_item(x = x, data = data, score = score, D = 1, fix.a.1pl = TRUE,
#> fix.g = TRUE, a.val.1pl = 1, g.val = 0.2, use.startval = FALSE)
#>
#> Summary of the Data
#> Number of Items in Response Data: 55
#> Number of Excluded Items: 0
#> Number of free parameters: 121
#> Number of Responses for Each Item:
#> id n
#> 1 CMC1 500
#> 2 CMC2 500
#> 3 CMC3 500
#> 4 CMC4 500
#> 5 CMC5 500
#> 6 CMC6 500
#> 7 CMC7 500
#> 8 CMC8 500
#> 9 CMC9 500
#> 10 CMC10 500
#> 11 CMC11 500
#> 12 CMC12 500
#> 13 CMC13 500
#> 14 CMC14 500
#> 15 CMC15 500
#> 16 CMC16 500
#> 17 CMC17 500
#> 18 CMC18 500
#> 19 CMC19 500
#> 20 CMC20 500
#> 21 CMC21 500
#> 22 CMC22 500
#> 23 CMC23 500
#> 24 CMC24 500
#> 25 CMC25 500
#> 26 CMC26 500
#> 27 CMC27 500
#> 28 CMC28 500
#> 29 CMC29 500
#> 30 CMC30 500
#> 31 CMC31 500
#> 32 CMC32 500
#> 33 CMC33 500
#> 34 CMC34 500
#> 35 CMC35 500
#> 36 CMC36 500
#> 37 CMC37 500
#> 38 CMC38 500
#> 39 CFR1 500
#> 40 CFR2 500
#> 41 AMC1 500
#> 42 AMC2 500
#> 43 AMC3 500
#> 44 AMC4 500
#> 45 AMC5 500
#> 46 AMC6 500
#> 47 AMC7 500
#> 48 AMC8 500
#> 49 AMC9 500
#> 50 AMC10 500
#> 51 AMC11 500
#> 52 AMC12 500
#> 53 AFR1 500
#> 54 AFR2 500
#> 55 AFR3 500
#>
#> Processing time (in seconds)
#> Total computation: 0.7
#>
#> Convergence of Solution
#> All item parameters were successfully converged.
#>
#> Summary of Estimation Results
#> -2loglikelihood: 31832.52
#> Item Parameters:
#> id cats model par.1 se.1 par.2 se.2 par.3 se.3 par.4 se.4
#> 1 CMC1 2 1PLM 1.00 NA 1.62 0.12 NA NA NA NA
#> 2 CMC2 2 1PLM 1.00 NA -1.08 0.11 NA NA NA NA
#> 3 CMC3 2 1PLM 1.00 NA 0.40 0.10 NA NA NA NA
#> 4 CMC4 2 2PLM 0.96 0.12 -0.43 0.11 NA NA NA NA
#> 5 CMC5 2 1PLM 1.00 NA -0.25 0.10 NA NA NA NA
#> 6 CMC6 2 3PLM 2.25 0.29 0.83 0.08 0.20 NA NA NA
#> 7 CMC7 2 3PLM 1.00 0.17 1.22 0.19 0.20 NA NA NA
#> 8 CMC8 2 2PLM 0.92 0.12 0.87 0.13 NA NA NA NA
#> 9 CMC9 2 2PLM 1.00 0.12 0.89 0.13 NA NA NA NA
#> 10 CMC10 2 2PLM 1.61 0.15 0.09 0.07 NA NA NA NA
#> 11 CMC11 2 2PLM 1.07 0.12 -0.37 0.10 NA NA NA NA
#> 12 CMC12 2 2PLM 0.94 0.12 1.10 0.15 NA NA NA NA
#> 13 CMC13 2 3PLM 1.53 0.28 1.37 0.15 0.20 NA NA NA
#> 14 CMC14 2 3PLM 1.26 0.18 0.05 0.10 0.20 NA NA NA
#> 15 CMC15 2 3PLM 1.52 0.20 0.00 0.09 0.20 NA NA NA
#> 16 CMC16 2 3PLM 2.36 0.27 0.18 0.07 0.20 NA NA NA
#> 17 CMC17 2 3PLM 1.06 0.15 -0.30 0.12 0.20 NA NA NA
#> 18 CMC18 2 3PLM 1.16 0.23 1.38 0.19 0.20 NA NA NA
#> 19 CMC19 2 3PLM 2.30 0.30 -1.07 0.10 0.20 NA NA NA
#> 20 CMC20 2 3PLM 1.48 0.22 -1.71 0.19 0.20 NA NA NA
#> 21 CMC21 2 3PLM 1.38 0.19 -1.25 0.16 0.20 NA NA NA
#> 22 CMC22 2 3PLM 0.93 0.14 -0.52 0.15 0.20 NA NA NA
#> 23 CMC23 2 3PLM 1.08 0.16 -0.17 0.12 0.20 NA NA NA
#> 24 CMC24 2 3PLM 1.13 0.23 1.40 0.19 0.20 NA NA NA
#> 25 CMC25 2 3PLM 0.82 0.15 -1.55 0.28 0.20 NA NA NA
#> 26 CMC26 2 3PLM 1.07 0.18 -2.14 0.31 0.20 NA NA NA
#> 27 CMC27 2 3PLM 1.27 0.17 0.22 0.10 0.20 NA NA NA
#> 28 CMC28 2 3PLM 2.22 0.27 -0.15 0.07 0.20 NA NA NA
#> 29 CMC29 2 3PLM 1.84 0.28 -1.19 0.14 0.20 NA NA NA
#> 30 CMC30 2 3PLM 1.19 0.20 0.35 0.11 0.20 NA NA NA
#> 31 CMC31 2 3PLM 0.76 0.15 1.15 0.23 0.20 NA NA NA
#> 32 CMC32 2 3PLM 1.62 0.22 -0.90 0.12 0.20 NA NA NA
#> 33 CMC33 2 3PLM 1.07 0.16 -1.43 0.21 0.20 NA NA NA
#> 34 CMC34 2 3PLM 1.11 0.16 0.33 0.12 0.20 NA NA NA
#> 35 CMC35 2 3PLM 1.42 0.18 -0.36 0.10 0.20 NA NA NA
#> 36 CMC36 2 3PLM 1.00 0.17 1.15 0.18 0.20 NA NA NA
#> 37 CMC37 2 3PLM 2.30 0.27 -0.15 0.07 0.20 NA NA NA
#> 38 CMC38 2 3PLM 0.87 0.14 -0.33 0.15 0.20 NA NA NA
#> 39 CFR1 5 GRM 2.00 0.14 -1.88 0.12 -1.25 0.08 -0.70 0.06
#> 40 CFR2 5 GRM 1.39 0.11 -0.80 0.09 -0.13 0.07 0.60 0.08
#> 41 AMC1 2 3PLM 1.45 0.22 0.57 0.10 0.20 NA NA NA
#> 42 AMC2 2 3PLM 1.72 0.25 -1.57 0.16 0.20 NA NA NA
#> 43 AMC3 2 3PLM 1.44 0.21 0.77 0.11 0.20 NA NA NA
#> 44 AMC4 2 3PLM 0.96 0.15 -0.13 0.13 0.20 NA NA NA
#> 45 AMC5 2 3PLM 1.83 0.53 2.10 0.25 0.20 NA NA NA
#> 46 AMC6 2 3PLM 3.32 0.68 1.50 0.09 0.20 NA NA NA
#> 47 AMC7 2 3PLM 1.48 0.21 0.25 0.09 0.20 NA NA NA
#> 48 AMC8 2 3PLM 1.65 0.23 0.39 0.09 0.20 NA NA NA
#> 49 AMC9 2 3PLM 1.72 0.23 0.59 0.09 0.20 NA NA NA
#> 50 AMC10 2 3PLM 3.21 0.62 1.40 0.09 0.20 NA NA NA
#> 51 AMC11 2 3PLM 1.78 0.22 -0.96 0.11 0.20 NA NA NA
#> 52 AMC12 2 3PLM 0.91 0.15 -0.96 0.19 0.20 NA NA NA
#> 53 AFR1 5 GRM 1.14 0.10 -0.30 0.09 0.30 0.09 0.92 0.11
#> 54 AFR2 5 GPCM 1.33 0.11 -1.99 0.21 -1.31 0.15 -0.72 0.12
#> 55 AFR3 5 GPCM 0.89 0.07 -0.80 0.15 0.15 0.15 0.46 0.16
#> par.5 se.5
#> 1 NA NA
#> 2 NA NA
#> 3 NA NA
#> 4 NA NA
#> 5 NA NA
#> 6 NA NA
#> 7 NA NA
#> 8 NA NA
#> 9 NA NA
#> 10 NA NA
#> 11 NA NA
#> 12 NA NA
#> 13 NA NA
#> 14 NA NA
#> 15 NA NA
#> 16 NA NA
#> 17 NA NA
#> 18 NA NA
#> 19 NA NA
#> 20 NA NA
#> 21 NA NA
#> 22 NA NA
#> 23 NA NA
#> 24 NA NA
#> 25 NA NA
#> 26 NA NA
#> 27 NA NA
#> 28 NA NA
#> 29 NA NA
#> 30 NA NA
#> 31 NA NA
#> 32 NA NA
#> 33 NA NA
#> 34 NA NA
#> 35 NA NA
#> 36 NA NA
#> 37 NA NA
#> 38 NA NA
#> 39 -0.23 0.06
#> 40 1.09 0.10
#> 41 NA NA
#> 42 NA NA
#> 43 NA NA
#> 44 NA NA
#> 45 NA NA
#> 46 NA NA
#> 47 NA NA
#> 48 NA NA
#> 49 NA NA
#> 50 NA NA
#> 51 NA NA
#> 52 NA NA
#> 53 1.35 0.13
#> 54 -0.21 0.10
#> 55 1.35 0.19
#>
#> Group Parameters:
#> mu sigma
#> 0.03 1.02
##----------------------------------------------------------------------------
# 3. The example code below shows how to prepare
# the data sets and how to conduct the IRT
# model-data fit analysis:
##----------------------------------------------------------------------------
## Step 1: prepare a data set for IRT In this
## example, we use the simulated mixed-item
## format CAT Data But, only items that have item
## responses more than 1,000 are assessed.
# find the location of items that have more than
# 1,000 item responses
over1000 <- which(colSums(simCAT_MX$res.dat, na.rm = TRUE) >
1000)
# (1) item metadata
x <- simCAT_MX$item.prm[over1000, ]
dim(x)
#> [1] 113 7
print(x[1:10, ])
#> id cats model par.1 par.2 par.3 par.4
#> 2 V2 2 2PLM 0.9152754 1.3843593 NA NA
#> 3 V3 2 2PLM 1.3454796 -1.2554919 NA NA
#> 5 V5 2 2PLM 1.0862914 1.7114409 NA NA
#> 6 V6 2 2PLM 1.1311496 -0.6029080 NA NA
#> 7 V7 2 2PLM 1.2012407 -0.4721664 NA NA
#> 8 V8 2 2PLM 1.3244155 -0.6353713 NA NA
#> 10 V10 2 2PLM 1.2487125 0.1381082 NA NA
#> 11 V11 2 2PLM 1.4413208 1.2276303 NA NA
#> 12 V12 2 2PLM 1.2077273 -0.8017795 NA NA
#> 13 V13 2 2PLM 1.1715456 -1.0803926 NA NA
# (2) examinee's ability estimates
score <- simCAT_MX$score
length(score)
#> [1] 30000
print(score[1:100])
#> [1] -0.30311440 -0.67224807 -0.73474583 1.76935738 -0.91017203 -0.28448278
#> [7] 0.81656431 -1.66434615 0.59312008 -0.35182937 0.23129679 -0.93107524
#> [13] -0.29971993 -0.32700449 -0.22271651 1.48912121 -0.92927809 0.43453041
#> [19] -0.01795450 -0.28365286 0.01115173 -0.76101441 0.12144273 0.83096135
#> [25] 1.96600585 -0.83510402 -0.40268865 -0.05605526 0.72398446 -0.16026059
#> [31] -1.09011778 1.22126764 -0.13340360 -1.28230720 -1.05581980 0.83484173
#> [37] -0.52136360 -0.66913590 -1.08580804 1.73214834 0.56950387 0.48016332
#> [43] -0.03472720 -2.17577824 0.44127032 0.98913071 1.43861714 -1.08133809
#> [49] -0.69016072 0.19325797 0.89998383 1.25383167 -1.09600809 0.50519143
#> [55] -0.51707395 -0.39474484 -0.45031102 1.85675021 1.50768131 1.06011811
#> [61] -0.41064797 1.10960278 -0.68853387 -0.59397660 -0.65326436 0.29147751
#> [67] -1.86787473 1.04838050 -1.14582092 1.07395234 -0.03828693 0.08445559
#> [73] 0.34582524 0.72300905 0.84448992 -1.86488055 0.77121937 1.66573208
#> [79] 0.10311673 -0.50768866 -1.60992457 -0.23074682 0.16162326 0.26091160
#> [85] 0.60682182 0.65415304 -0.69923141 1.07545766 0.24060267 -0.93542383
#> [91] 1.24988766 -0.01826940 1.27403936 0.10985621 -1.19092047 0.79614598
#> [97] 0.62302338 -0.89455596 -0.03472720 0.20250837
# (3) response data
data <- simCAT_MX$res.dat[, over1000]
dim(data)
#> [1] 30000 113
print(data[1:20, 1:6])
#> Item.dc.2 Item.dc.3 Item.dc.5 Item.dc.6 Item.dc.7 Item.dc.8
#> [1,] NA NA NA NA 0 1
#> [2,] NA NA NA NA 0 1
#> [3,] NA NA NA NA 1 1
#> [4,] NA NA 0 NA NA NA
#> [5,] NA 1 NA 0 1 1
#> [6,] NA 0 NA 0 1 0
#> [7,] NA NA NA NA NA NA
#> [8,] NA 1 NA 1 1 0
#> [9,] NA NA 0 NA NA NA
#> [10,] NA 0 NA 1 1 0
#> [11,] NA NA 0 NA NA NA
#> [12,] NA 1 NA 0 1 1
#> [13,] NA 0 NA 1 1 0
#> [14,] NA NA NA NA 1 NA
#> [15,] NA NA NA 1 1 1
#> [16,] 1 NA 0 NA NA NA
#> [17,] NA 0 NA 0 1 0
#> [18,] NA NA NA NA NA NA
#> [19,] NA 0 NA 0 1 1
#> [20,] NA NA NA NA NA NA
## Step 2: Compute the IRT mode-data fit
## statistics (1) the use of 'equal.width'
fit1 <- irtfit(x = x, score = score, data = data, group.method = "equal.width",
n.width = 11, loc.theta = "average", range.score = c(-4,
4), D = 1, alpha = 0.05, missing = NA, overSR = 2.5)
# what kinds of internal objects does the results
# have?
names(fit1)
#> [1] "fit_stat" "contingency.fitstat" "contingency.plot"
#> [4] "item_df" "individual.info" "ancillary"
#> [7] "call"
# show the results of the fit statistics
fit1$fit_stat[1:10, ]
#> id X2 G2 df.X2 df.G2 crit.val.X2 crit.val.G2 p.X2 p.G2 outfit
#> 1 V2 75.070 75.209 8 10 15.51 18.31 0 0 1.018
#> 2 V3 186.880 168.082 8 10 15.51 18.31 0 0 1.124
#> 3 V5 151.329 139.213 8 10 15.51 18.31 0 0 1.133
#> 4 V6 178.409 157.911 8 10 15.51 18.31 0 0 1.056
#> 5 V7 185.438 170.360 9 11 16.92 19.68 0 0 1.078
#> 6 V8 209.653 193.001 8 10 15.51 18.31 0 0 1.098
#> 7 V10 267.444 239.563 9 11 16.92 19.68 0 0 1.097
#> 8 V11 148.896 133.209 7 9 14.07 16.92 0 0 1.129
#> 9 V12 139.295 125.647 9 11 16.92 19.68 0 0 1.065
#> 10 V13 128.422 117.439 9 11 16.92 19.68 0 0 1.075
#> infit N overSR.prop
#> 1 1.016 2018 0.364
#> 2 1.090 11041 0.636
#> 3 1.111 5181 0.727
#> 4 1.045 13599 0.545
#> 5 1.059 18293 0.455
#> 6 1.075 16163 0.636
#> 7 1.073 19702 0.727
#> 8 1.083 13885 0.455
#> 9 1.051 12118 0.636
#> 10 1.059 10719 0.545
# show the contingency tables for the first item
# (dichotomous)
fit1$contingency.fitstat[[1]]
#> total obs.freq.0 obs.freq.1 exp.freq.0 exp.freq.1 obs.prop.0 obs.prop.1
#> 1 8 5 3 6.102331 1.897669 0.6250000 0.3750000
#> 2 14 8 6 9.969510 4.030490 0.5714286 0.4285714
#> 3 60 34 26 40.253757 19.746243 0.5666667 0.4333333
#> 4 185 99 86 115.264928 69.735072 0.5351351 0.4648649
#> 5 240 115 125 138.368078 101.631922 0.4791667 0.5208333
#> 6 349 145 204 185.031440 163.968560 0.4154728 0.5845272
#> 7 325 114 211 155.483116 169.516884 0.3507692 0.6492308
#> 8 246 82 164 108.731822 137.268178 0.3333333 0.6666667
#> 9 377 139 238 154.062263 222.937737 0.3687003 0.6312997
#> 10 214 78 136 72.645447 141.354553 0.3644860 0.6355140
#> exp.prob.0 exp.prob.1 raw.rsd.0 raw.rsd.1
#> 1 0.7627914 0.2372086 -0.13779141 0.13779141
#> 2 0.7121079 0.2878921 -0.14067932 0.14067932
#> 3 0.6708959 0.3291041 -0.10422928 0.10422928
#> 4 0.6230537 0.3769463 -0.08791853 0.08791853
#> 5 0.5765337 0.4234663 -0.09736699 0.09736699
#> 6 0.5301760 0.4698240 -0.11470327 0.11470327
#> 7 0.4784096 0.5215904 -0.12764036 0.12764036
#> 8 0.4419993 0.5580007 -0.10866594 0.10866594
#> 9 0.4086532 0.5913468 -0.03995295 0.03995295
#> 10 0.3394647 0.6605353 0.02502128 -0.02502128
# (2) the use of 'equal.freq'
fit2 <- irtfit(x = x, score = score, data = data, group.method = "equal.freq",
n.width = 11, loc.theta = "average", range.score = c(-4,
4), D = 1, alpha = 0.05, missing = NA)
# show the results of the fit statistics
fit2$fit_stat[1:10, ]
#> id X2 G2 df.X2 df.G2 crit.val.X2 crit.val.G2 p.X2 p.G2 outfit
#> 1 V2 77.967 78.144 9 11 16.92 19.68 0 0 1.018
#> 2 V3 202.035 181.832 9 11 16.92 19.68 0 0 1.124
#> 3 V5 146.383 135.908 9 11 16.92 19.68 0 0 1.133
#> 4 V6 140.038 133.287 9 11 16.92 19.68 0 0 1.056
#> 5 V7 188.814 177.526 9 11 16.92 19.68 0 0 1.078
#> 6 V8 211.279 196.328 9 11 16.92 19.68 0 0 1.098
#> 7 V10 259.669 239.292 9 11 16.92 19.68 0 0 1.097
#> 8 V11 166.427 150.419 9 11 16.92 19.68 0 0 1.129
#> 9 V12 145.789 134.690 9 11 16.92 19.68 0 0 1.065
#> 10 V13 141.283 132.270 9 11 16.92 19.68 0 0 1.075
#> infit N overSR.prop
#> 1 1.016 2018 0.727
#> 2 1.090 11041 0.636
#> 3 1.111 5181 0.727
#> 4 1.045 13599 0.545
#> 5 1.059 18293 0.455
#> 6 1.075 16163 0.545
#> 7 1.073 19702 0.636
#> 8 1.083 13885 0.636
#> 9 1.051 12118 0.364
#> 10 1.059 10719 0.636
# show the contingency table for the fourth item
# (polytomous)
fit2$contingency.fitstat[[4]]
#> total obs.freq.0 obs.freq.1 exp.freq.0 exp.freq.1 obs.prop.0 obs.prop.1
#> 1 1241 967 274 997.5790 243.4210 0.7792103 0.2207897
#> 2 1243 879 364 890.2108 352.7892 0.7071601 0.2928399
#> 3 1243 784 459 817.3780 425.6220 0.6307321 0.3692679
#> 4 1219 747 472 737.4210 481.5790 0.6127974 0.3872026
#> 5 1236 705 531 693.8229 542.1771 0.5703883 0.4296117
#> 6 1243 677 566 656.2493 586.7507 0.5446500 0.4553500
#> 7 1270 662 608 625.5502 644.4498 0.5212598 0.4787402
#> 8 1230 616 614 552.4864 677.5136 0.5008130 0.4991870
#> 9 1207 553 654 486.1543 720.8457 0.4581607 0.5418393
#> 10 1233 494 739 432.6918 800.3082 0.4006488 0.5993512
#> 11 1234 465 769 324.5644 909.4356 0.3768233 0.6231767
#> exp.prob.0 exp.prob.1 raw.rsd.0 raw.rsd.1
#> 1 0.8038510 0.1961490 -0.024640641 0.024640641
#> 2 0.7161793 0.2838207 -0.009019180 0.009019180
#> 3 0.6575849 0.3424151 -0.026852795 0.026852795
#> 4 0.6049393 0.3950607 0.007858099 -0.007858099
#> 5 0.5613454 0.4386546 0.009042942 -0.009042942
#> 6 0.5279560 0.4720440 0.016694048 -0.016694048
#> 7 0.4925592 0.5074408 0.028700633 -0.028700633
#> 8 0.4491759 0.5508241 0.051637085 -0.051637085
#> 9 0.4027790 0.5972210 0.055381721 -0.055381721
#> 10 0.3509261 0.6490739 0.049722759 -0.049722759
#> 11 0.2630181 0.7369819 0.113805214 -0.113805214
## Step 3: Draw the IRT residual plots 1. the
## dichotomous item (1) both raw and standardized
## residual plots using the object 'fit1'
plot(x = fit1, item.loc = 1, type = "both", ci.method = "wald",
ylim.sr.adjust = TRUE)
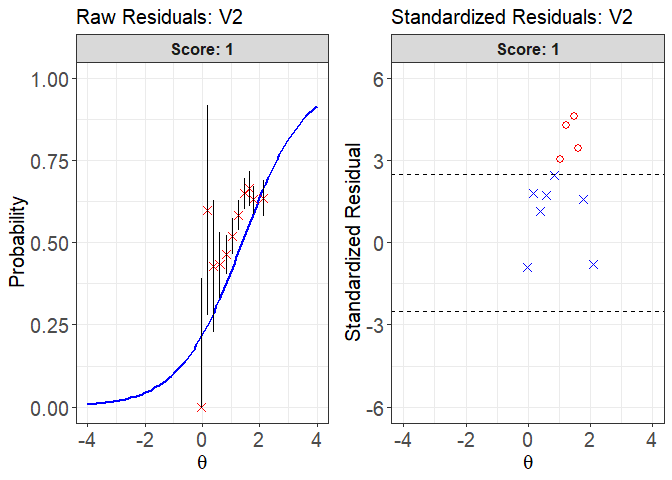
#> interval point total obs.freq.0 obs.freq.1 obs.prop.0
#> 1 [-0.1218815,0.08512996] -0.02529272 3 3 0 1.0000000
#> 2 (0.08512996,0.2921415] 0.18431014 5 2 3 0.4000000
#> 3 (0.2921415,0.499153] 0.39488272 14 8 6 0.5714286
#> 4 (0.499153,0.7061645] 0.60618911 60 34 26 0.5666667
#> 5 (0.7061645,0.913176] 0.83531169 185 99 86 0.5351351
#> 6 (0.913176,1.120187] 1.04723712 240 115 125 0.4791667
#> 7 (1.120187,1.327199] 1.25232143 349 145 204 0.4154728
#> 8 (1.327199,1.53421] 1.47877397 325 114 211 0.3507692
#> 9 (1.53421,1.741222] 1.63898436 246 82 164 0.3333333
#> 10 (1.741222,1.948233] 1.78810197 377 139 238 0.3687003
#> 11 (1.948233,2.155245] 2.11166019 214 78 136 0.3644860
#> obs.prop.1 exp.prob.0 exp.prob.1 raw.rsd.0 raw.rsd.1 se.0
#> 1 0.0000000 0.7841844 0.2158156 0.21581559 -0.21581559 0.23751437
#> 2 0.6000000 0.7499556 0.2500444 -0.34995561 0.34995561 0.19366063
#> 3 0.4285714 0.7121079 0.2878921 -0.14067932 0.14067932 0.12101070
#> 4 0.4333333 0.6708959 0.3291041 -0.10422928 0.10422928 0.06066226
#> 5 0.4648649 0.6230537 0.3769463 -0.08791853 0.08791853 0.03563007
#> 6 0.5208333 0.5765337 0.4234663 -0.09736699 0.09736699 0.03189453
#> 7 0.5845272 0.5301760 0.4698240 -0.11470327 0.11470327 0.02671560
#> 8 0.6492308 0.4784096 0.5215904 -0.12764036 0.12764036 0.02770914
#> 9 0.6666667 0.4419993 0.5580007 -0.10866594 0.10866594 0.03166362
#> 10 0.6312997 0.4086532 0.5913468 -0.03995295 0.03995295 0.02531791
#> 11 0.6355140 0.3394647 0.6605353 0.02502128 -0.02502128 0.03236968
#> se.1 std.rsd.0 std.rsd.1
#> 1 0.23751437 0.9086423 -0.9086423
#> 2 0.19366063 -1.8070560 1.8070560
#> 3 0.12101070 -1.1625362 1.1625362
#> 4 0.06066226 -1.7181899 1.7181899
#> 5 0.03563007 -2.4675377 2.4675377
#> 6 0.03189453 -3.0527806 3.0527806
#> 7 0.02671560 -4.2934941 4.2934941
#> 8 0.02770914 -4.6064351 4.6064351
#> 9 0.03166362 -3.4318859 3.4318859
#> 10 0.02531791 -1.5780508 1.5780508
#> 11 0.03236968 0.7729850 -0.7729850
# (2) the raw residual plots using the object
# 'fit1'
plot(x = fit1, item.loc = 1, type = "icc", ci.method = "wald",
ylim.sr.adjust = TRUE)
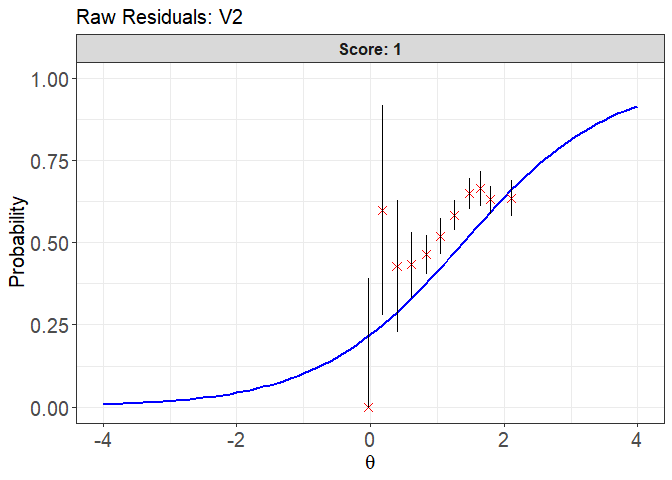
#> interval point total obs.freq.0 obs.freq.1 obs.prop.0
#> 1 [-0.1218815,0.08512996] -0.02529272 3 3 0 1.0000000
#> 2 (0.08512996,0.2921415] 0.18431014 5 2 3 0.4000000
#> 3 (0.2921415,0.499153] 0.39488272 14 8 6 0.5714286
#> 4 (0.499153,0.7061645] 0.60618911 60 34 26 0.5666667
#> 5 (0.7061645,0.913176] 0.83531169 185 99 86 0.5351351
#> 6 (0.913176,1.120187] 1.04723712 240 115 125 0.4791667
#> 7 (1.120187,1.327199] 1.25232143 349 145 204 0.4154728
#> 8 (1.327199,1.53421] 1.47877397 325 114 211 0.3507692
#> 9 (1.53421,1.741222] 1.63898436 246 82 164 0.3333333
#> 10 (1.741222,1.948233] 1.78810197 377 139 238 0.3687003
#> 11 (1.948233,2.155245] 2.11166019 214 78 136 0.3644860
#> obs.prop.1 exp.prob.0 exp.prob.1 raw.rsd.0 raw.rsd.1 se.0
#> 1 0.0000000 0.7841844 0.2158156 0.21581559 -0.21581559 0.23751437
#> 2 0.6000000 0.7499556 0.2500444 -0.34995561 0.34995561 0.19366063
#> 3 0.4285714 0.7121079 0.2878921 -0.14067932 0.14067932 0.12101070
#> 4 0.4333333 0.6708959 0.3291041 -0.10422928 0.10422928 0.06066226
#> 5 0.4648649 0.6230537 0.3769463 -0.08791853 0.08791853 0.03563007
#> 6 0.5208333 0.5765337 0.4234663 -0.09736699 0.09736699 0.03189453
#> 7 0.5845272 0.5301760 0.4698240 -0.11470327 0.11470327 0.02671560
#> 8 0.6492308 0.4784096 0.5215904 -0.12764036 0.12764036 0.02770914
#> 9 0.6666667 0.4419993 0.5580007 -0.10866594 0.10866594 0.03166362
#> 10 0.6312997 0.4086532 0.5913468 -0.03995295 0.03995295 0.02531791
#> 11 0.6355140 0.3394647 0.6605353 0.02502128 -0.02502128 0.03236968
#> se.1 std.rsd.0 std.rsd.1
#> 1 0.23751437 0.9086423 -0.9086423
#> 2 0.19366063 -1.8070560 1.8070560
#> 3 0.12101070 -1.1625362 1.1625362
#> 4 0.06066226 -1.7181899 1.7181899
#> 5 0.03563007 -2.4675377 2.4675377
#> 6 0.03189453 -3.0527806 3.0527806
#> 7 0.02671560 -4.2934941 4.2934941
#> 8 0.02770914 -4.6064351 4.6064351
#> 9 0.03166362 -3.4318859 3.4318859
#> 10 0.02531791 -1.5780508 1.5780508
#> 11 0.03236968 0.7729850 -0.7729850
# (3) the standardized residual plots using the
# object 'fit1'
plot(x = fit1, item.loc = 113, type = "sr", ci.method = "wald",
ylim.sr.adjust = TRUE)
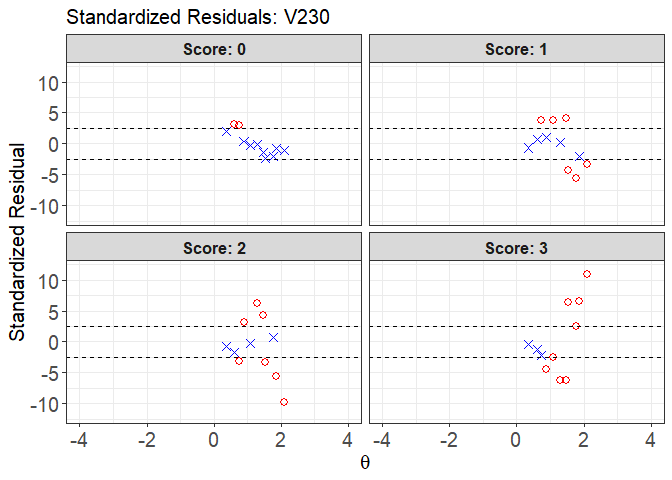
#> interval point total obs.freq.0 obs.freq.1 obs.freq.2
#> 1 [0.3564295,0.5199582] 0.3564295 1 1 0 0
#> 2 (0.5199582,0.6834869] 0.6081321 5 3 2 0
#> 3 (0.6834869,0.8470155] 0.7400138 15 5 10 0
#> 4 (0.8470155,1.010544] 0.8866202 55 5 15 34
#> 5 (1.010544,1.174073] 1.0821064 133 6 40 53
#> 6 (1.174073,1.337602] 1.2832293 260 8 37 153
#> 7 (1.337602,1.50113] 1.4747336 98 0 23 57
#> 8 (1.50113,1.664659] 1.5311735 306 0 7 85
#> 9 (1.664659,1.828188] 1.7632607 418 0 0 145
#> 10 (1.828188,1.991716] 1.8577191 69 0 0 0
#> 11 (1.991716,2.155245] 2.1021956 263 0 0 0
#> obs.freq.3 obs.prop.0 obs.prop.1 obs.prop.2 obs.prop.3 exp.prob.0
#> 1 0 1.00000000 0.00000000 0.0000000 0.00000000 0.196511833
#> 2 0 0.60000000 0.40000000 0.0000000 0.00000000 0.130431315
#> 3 0 0.33333333 0.66666667 0.0000000 0.00000000 0.102631449
#> 4 1 0.09090909 0.27272727 0.6181818 0.01818182 0.077129446
#> 5 34 0.04511278 0.30075188 0.3984962 0.25563910 0.051169395
#> 6 62 0.03076923 0.14230769 0.5884615 0.23846154 0.032494074
#> 7 18 0.00000000 0.23469388 0.5816327 0.18367347 0.020534959
#> 8 214 0.00000000 0.02287582 0.2777778 0.69934641 0.017857642
#> 9 273 0.00000000 0.00000000 0.3468900 0.65311005 0.009866868
#> 10 69 0.00000000 0.00000000 0.0000000 1.00000000 0.007690015
#> 11 263 0.00000000 0.00000000 0.0000000 1.00000000 0.003962699
#> exp.prob.1 exp.prob.2 exp.prob.3 raw.rsd.0 raw.rsd.1 raw.rsd.2
#> 1 0.31299790 0.3472692 0.1432210 0.803488167 -0.312997903 -0.34726922
#> 2 0.27025065 0.3900531 0.2092649 0.469568685 0.129749354 -0.39005312
#> 3 0.24407213 0.4043226 0.2489738 0.230701885 0.422594537 -0.40432265
#> 4 0.21379299 0.4127992 0.2962784 0.013779645 0.058934282 0.20538261
#> 5 0.17398130 0.4120662 0.3627831 -0.006056613 0.126770584 -0.01356995
#> 6 0.13632441 0.3983962 0.4327853 -0.001724843 0.005983284 0.19006531
#> 7 0.10523862 0.3756891 0.4985373 -0.020534959 0.129455259 0.20594357
#> 8 0.09707782 0.3676106 0.5174539 -0.017857642 -0.074201998 -0.08983281
#> 9 0.06836048 0.3299158 0.5918569 -0.009866868 -0.068360484 0.01697418
#> 10 0.05880602 0.3132481 0.6202558 -0.007690015 -0.058806016 -0.31324812
#> 11 0.03912356 0.2690653 0.6878484 -0.003962699 -0.039123555 -0.26906531
#> raw.rsd.3 se.0 se.1 se.2 se.3 std.rsd.0
#> 1 -0.14322104 0.397359953 0.46371351 0.47610220 0.35029812 2.0220663
#> 2 -0.20926492 0.150611412 0.19860274 0.21813376 0.18191928 3.1177497
#> 3 -0.24897378 0.078357401 0.11090564 0.12671381 0.11165000 2.9442258
#> 4 -0.27809653 0.035974863 0.05528201 0.06638675 0.06156999 0.3830354
#> 5 -0.10714402 0.019106171 0.03287157 0.04267975 0.04169091 -0.3169978
#> 6 -0.19432375 0.010996190 0.02128019 0.03036171 0.03072722 -0.1568583
#> 7 -0.31486387 0.014326112 0.03099761 0.04892172 0.05050741 -1.4333937
#> 8 0.18189246 0.007570744 0.01692484 0.02756294 0.02856568 -2.3587698
#> 9 0.06125317 0.004834464 0.01234350 0.02299737 0.02403956 -2.0409436
#> 10 0.37974416 0.010516294 0.02832213 0.05583668 0.05842604 -0.7312476
#> 11 0.31215156 0.003873963 0.01195570 0.02734578 0.02857270 -1.0229057
#> std.rsd.1 std.rsd.2 std.rsd.3
#> 1 -0.6749812 -0.7294006 -0.4088547
#> 2 0.6533110 -1.7881373 -1.1503175
#> 3 3.8103971 -3.1908333 -2.2299488
#> 4 1.0660662 3.0937290 -4.5167547
#> 5 3.8565422 -0.3179482 -2.5699613
#> 6 0.2811669 6.2600333 -6.3241558
#> 7 4.1762987 4.2096551 -6.2340132
#> 8 -4.3842081 -3.2591881 6.3675177
#> 9 -5.5381760 0.7380923 2.5480159
#> 10 -2.0763275 -5.6100775 6.4995706
#> 11 -3.2723764 -9.8393733 10.9248190
# 2. the polytomous item (1) both raw and
# standardized residual plots using the object
# 'fit1'
plot(x = fit1, item.loc = 113, type = "both", ci.method = "wald",
ylim.sr.adjust = TRUE)
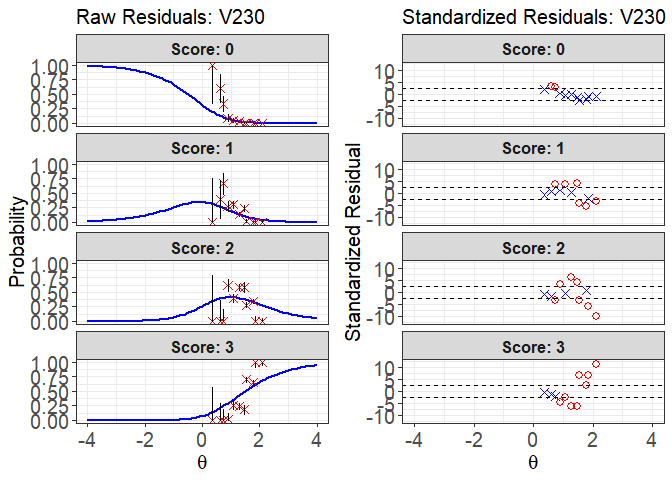
#> interval point total obs.freq.0 obs.freq.1 obs.freq.2
#> 1 [0.3564295,0.5199582] 0.3564295 1 1 0 0
#> 2 (0.5199582,0.6834869] 0.6081321 5 3 2 0
#> 3 (0.6834869,0.8470155] 0.7400138 15 5 10 0
#> 4 (0.8470155,1.010544] 0.8866202 55 5 15 34
#> 5 (1.010544,1.174073] 1.0821064 133 6 40 53
#> 6 (1.174073,1.337602] 1.2832293 260 8 37 153
#> 7 (1.337602,1.50113] 1.4747336 98 0 23 57
#> 8 (1.50113,1.664659] 1.5311735 306 0 7 85
#> 9 (1.664659,1.828188] 1.7632607 418 0 0 145
#> 10 (1.828188,1.991716] 1.8577191 69 0 0 0
#> 11 (1.991716,2.155245] 2.1021956 263 0 0 0
#> obs.freq.3 obs.prop.0 obs.prop.1 obs.prop.2 obs.prop.3 exp.prob.0
#> 1 0 1.00000000 0.00000000 0.0000000 0.00000000 0.196511833
#> 2 0 0.60000000 0.40000000 0.0000000 0.00000000 0.130431315
#> 3 0 0.33333333 0.66666667 0.0000000 0.00000000 0.102631449
#> 4 1 0.09090909 0.27272727 0.6181818 0.01818182 0.077129446
#> 5 34 0.04511278 0.30075188 0.3984962 0.25563910 0.051169395
#> 6 62 0.03076923 0.14230769 0.5884615 0.23846154 0.032494074
#> 7 18 0.00000000 0.23469388 0.5816327 0.18367347 0.020534959
#> 8 214 0.00000000 0.02287582 0.2777778 0.69934641 0.017857642
#> 9 273 0.00000000 0.00000000 0.3468900 0.65311005 0.009866868
#> 10 69 0.00000000 0.00000000 0.0000000 1.00000000 0.007690015
#> 11 263 0.00000000 0.00000000 0.0000000 1.00000000 0.003962699
#> exp.prob.1 exp.prob.2 exp.prob.3 raw.rsd.0 raw.rsd.1 raw.rsd.2
#> 1 0.31299790 0.3472692 0.1432210 0.803488167 -0.312997903 -0.34726922
#> 2 0.27025065 0.3900531 0.2092649 0.469568685 0.129749354 -0.39005312
#> 3 0.24407213 0.4043226 0.2489738 0.230701885 0.422594537 -0.40432265
#> 4 0.21379299 0.4127992 0.2962784 0.013779645 0.058934282 0.20538261
#> 5 0.17398130 0.4120662 0.3627831 -0.006056613 0.126770584 -0.01356995
#> 6 0.13632441 0.3983962 0.4327853 -0.001724843 0.005983284 0.19006531
#> 7 0.10523862 0.3756891 0.4985373 -0.020534959 0.129455259 0.20594357
#> 8 0.09707782 0.3676106 0.5174539 -0.017857642 -0.074201998 -0.08983281
#> 9 0.06836048 0.3299158 0.5918569 -0.009866868 -0.068360484 0.01697418
#> 10 0.05880602 0.3132481 0.6202558 -0.007690015 -0.058806016 -0.31324812
#> 11 0.03912356 0.2690653 0.6878484 -0.003962699 -0.039123555 -0.26906531
#> raw.rsd.3 se.0 se.1 se.2 se.3 std.rsd.0
#> 1 -0.14322104 0.397359953 0.46371351 0.47610220 0.35029812 2.0220663
#> 2 -0.20926492 0.150611412 0.19860274 0.21813376 0.18191928 3.1177497
#> 3 -0.24897378 0.078357401 0.11090564 0.12671381 0.11165000 2.9442258
#> 4 -0.27809653 0.035974863 0.05528201 0.06638675 0.06156999 0.3830354
#> 5 -0.10714402 0.019106171 0.03287157 0.04267975 0.04169091 -0.3169978
#> 6 -0.19432375 0.010996190 0.02128019 0.03036171 0.03072722 -0.1568583
#> 7 -0.31486387 0.014326112 0.03099761 0.04892172 0.05050741 -1.4333937
#> 8 0.18189246 0.007570744 0.01692484 0.02756294 0.02856568 -2.3587698
#> 9 0.06125317 0.004834464 0.01234350 0.02299737 0.02403956 -2.0409436
#> 10 0.37974416 0.010516294 0.02832213 0.05583668 0.05842604 -0.7312476
#> 11 0.31215156 0.003873963 0.01195570 0.02734578 0.02857270 -1.0229057
#> std.rsd.1 std.rsd.2 std.rsd.3
#> 1 -0.6749812 -0.7294006 -0.4088547
#> 2 0.6533110 -1.7881373 -1.1503175
#> 3 3.8103971 -3.1908333 -2.2299488
#> 4 1.0660662 3.0937290 -4.5167547
#> 5 3.8565422 -0.3179482 -2.5699613
#> 6 0.2811669 6.2600333 -6.3241558
#> 7 4.1762987 4.2096551 -6.2340132
#> 8 -4.3842081 -3.2591881 6.3675177
#> 9 -5.5381760 0.7380923 2.5480159
#> 10 -2.0763275 -5.6100775 6.4995706
#> 11 -3.2723764 -9.8393733 10.9248190
# (2) the raw residual plots using the object
# 'fit1'
plot(x = fit1, item.loc = 113, type = "icc", ci.method = "wald",
layout.col = 2, ylim.sr.adjust = TRUE)
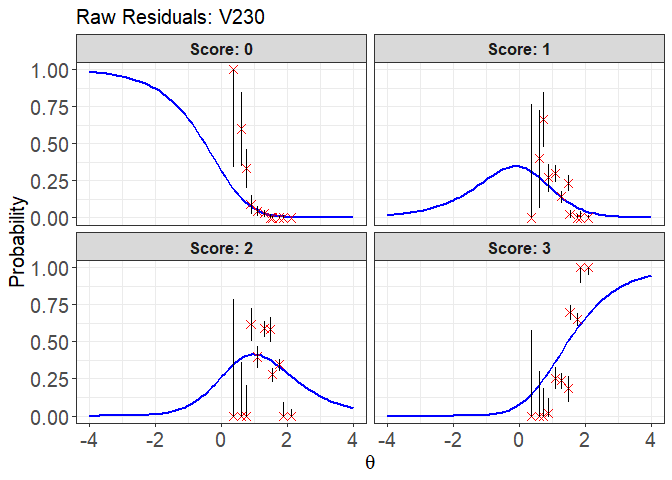
#> interval point total obs.freq.0 obs.freq.1 obs.freq.2
#> 1 [0.3564295,0.5199582] 0.3564295 1 1 0 0
#> 2 (0.5199582,0.6834869] 0.6081321 5 3 2 0
#> 3 (0.6834869,0.8470155] 0.7400138 15 5 10 0
#> 4 (0.8470155,1.010544] 0.8866202 55 5 15 34
#> 5 (1.010544,1.174073] 1.0821064 133 6 40 53
#> 6 (1.174073,1.337602] 1.2832293 260 8 37 153
#> 7 (1.337602,1.50113] 1.4747336 98 0 23 57
#> 8 (1.50113,1.664659] 1.5311735 306 0 7 85
#> 9 (1.664659,1.828188] 1.7632607 418 0 0 145
#> 10 (1.828188,1.991716] 1.8577191 69 0 0 0
#> 11 (1.991716,2.155245] 2.1021956 263 0 0 0
#> obs.freq.3 obs.prop.0 obs.prop.1 obs.prop.2 obs.prop.3 exp.prob.0
#> 1 0 1.00000000 0.00000000 0.0000000 0.00000000 0.196511833
#> 2 0 0.60000000 0.40000000 0.0000000 0.00000000 0.130431315
#> 3 0 0.33333333 0.66666667 0.0000000 0.00000000 0.102631449
#> 4 1 0.09090909 0.27272727 0.6181818 0.01818182 0.077129446
#> 5 34 0.04511278 0.30075188 0.3984962 0.25563910 0.051169395
#> 6 62 0.03076923 0.14230769 0.5884615 0.23846154 0.032494074
#> 7 18 0.00000000 0.23469388 0.5816327 0.18367347 0.020534959
#> 8 214 0.00000000 0.02287582 0.2777778 0.69934641 0.017857642
#> 9 273 0.00000000 0.00000000 0.3468900 0.65311005 0.009866868
#> 10 69 0.00000000 0.00000000 0.0000000 1.00000000 0.007690015
#> 11 263 0.00000000 0.00000000 0.0000000 1.00000000 0.003962699
#> exp.prob.1 exp.prob.2 exp.prob.3 raw.rsd.0 raw.rsd.1 raw.rsd.2
#> 1 0.31299790 0.3472692 0.1432210 0.803488167 -0.312997903 -0.34726922
#> 2 0.27025065 0.3900531 0.2092649 0.469568685 0.129749354 -0.39005312
#> 3 0.24407213 0.4043226 0.2489738 0.230701885 0.422594537 -0.40432265
#> 4 0.21379299 0.4127992 0.2962784 0.013779645 0.058934282 0.20538261
#> 5 0.17398130 0.4120662 0.3627831 -0.006056613 0.126770584 -0.01356995
#> 6 0.13632441 0.3983962 0.4327853 -0.001724843 0.005983284 0.19006531
#> 7 0.10523862 0.3756891 0.4985373 -0.020534959 0.129455259 0.20594357
#> 8 0.09707782 0.3676106 0.5174539 -0.017857642 -0.074201998 -0.08983281
#> 9 0.06836048 0.3299158 0.5918569 -0.009866868 -0.068360484 0.01697418
#> 10 0.05880602 0.3132481 0.6202558 -0.007690015 -0.058806016 -0.31324812
#> 11 0.03912356 0.2690653 0.6878484 -0.003962699 -0.039123555 -0.26906531
#> raw.rsd.3 se.0 se.1 se.2 se.3 std.rsd.0
#> 1 -0.14322104 0.397359953 0.46371351 0.47610220 0.35029812 2.0220663
#> 2 -0.20926492 0.150611412 0.19860274 0.21813376 0.18191928 3.1177497
#> 3 -0.24897378 0.078357401 0.11090564 0.12671381 0.11165000 2.9442258
#> 4 -0.27809653 0.035974863 0.05528201 0.06638675 0.06156999 0.3830354
#> 5 -0.10714402 0.019106171 0.03287157 0.04267975 0.04169091 -0.3169978
#> 6 -0.19432375 0.010996190 0.02128019 0.03036171 0.03072722 -0.1568583
#> 7 -0.31486387 0.014326112 0.03099761 0.04892172 0.05050741 -1.4333937
#> 8 0.18189246 0.007570744 0.01692484 0.02756294 0.02856568 -2.3587698
#> 9 0.06125317 0.004834464 0.01234350 0.02299737 0.02403956 -2.0409436
#> 10 0.37974416 0.010516294 0.02832213 0.05583668 0.05842604 -0.7312476
#> 11 0.31215156 0.003873963 0.01195570 0.02734578 0.02857270 -1.0229057
#> std.rsd.1 std.rsd.2 std.rsd.3
#> 1 -0.6749812 -0.7294006 -0.4088547
#> 2 0.6533110 -1.7881373 -1.1503175
#> 3 3.8103971 -3.1908333 -2.2299488
#> 4 1.0660662 3.0937290 -4.5167547
#> 5 3.8565422 -0.3179482 -2.5699613
#> 6 0.2811669 6.2600333 -6.3241558
#> 7 4.1762987 4.2096551 -6.2340132
#> 8 -4.3842081 -3.2591881 6.3675177
#> 9 -5.5381760 0.7380923 2.5480159
#> 10 -2.0763275 -5.6100775 6.4995706
#> 11 -3.2723764 -9.8393733 10.9248190
# (3) the standardized residual plots using the
# object 'fit1'
plot(x = fit1, item.loc = 113, type = "sr", ci.method = "wald",
layout.col = 4, ylim.sr.adjust = TRUE)
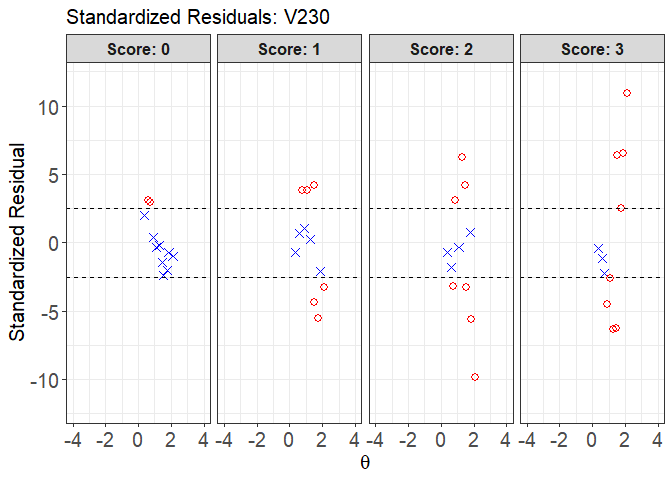
#> interval point total obs.freq.0 obs.freq.1 obs.freq.2
#> 1 [0.3564295,0.5199582] 0.3564295 1 1 0 0
#> 2 (0.5199582,0.6834869] 0.6081321 5 3 2 0
#> 3 (0.6834869,0.8470155] 0.7400138 15 5 10 0
#> 4 (0.8470155,1.010544] 0.8866202 55 5 15 34
#> 5 (1.010544,1.174073] 1.0821064 133 6 40 53
#> 6 (1.174073,1.337602] 1.2832293 260 8 37 153
#> 7 (1.337602,1.50113] 1.4747336 98 0 23 57
#> 8 (1.50113,1.664659] 1.5311735 306 0 7 85
#> 9 (1.664659,1.828188] 1.7632607 418 0 0 145
#> 10 (1.828188,1.991716] 1.8577191 69 0 0 0
#> 11 (1.991716,2.155245] 2.1021956 263 0 0 0
#> obs.freq.3 obs.prop.0 obs.prop.1 obs.prop.2 obs.prop.3 exp.prob.0
#> 1 0 1.00000000 0.00000000 0.0000000 0.00000000 0.196511833
#> 2 0 0.60000000 0.40000000 0.0000000 0.00000000 0.130431315
#> 3 0 0.33333333 0.66666667 0.0000000 0.00000000 0.102631449
#> 4 1 0.09090909 0.27272727 0.6181818 0.01818182 0.077129446
#> 5 34 0.04511278 0.30075188 0.3984962 0.25563910 0.051169395
#> 6 62 0.03076923 0.14230769 0.5884615 0.23846154 0.032494074
#> 7 18 0.00000000 0.23469388 0.5816327 0.18367347 0.020534959
#> 8 214 0.00000000 0.02287582 0.2777778 0.69934641 0.017857642
#> 9 273 0.00000000 0.00000000 0.3468900 0.65311005 0.009866868
#> 10 69 0.00000000 0.00000000 0.0000000 1.00000000 0.007690015
#> 11 263 0.00000000 0.00000000 0.0000000 1.00000000 0.003962699
#> exp.prob.1 exp.prob.2 exp.prob.3 raw.rsd.0 raw.rsd.1 raw.rsd.2
#> 1 0.31299790 0.3472692 0.1432210 0.803488167 -0.312997903 -0.34726922
#> 2 0.27025065 0.3900531 0.2092649 0.469568685 0.129749354 -0.39005312
#> 3 0.24407213 0.4043226 0.2489738 0.230701885 0.422594537 -0.40432265
#> 4 0.21379299 0.4127992 0.2962784 0.013779645 0.058934282 0.20538261
#> 5 0.17398130 0.4120662 0.3627831 -0.006056613 0.126770584 -0.01356995
#> 6 0.13632441 0.3983962 0.4327853 -0.001724843 0.005983284 0.19006531
#> 7 0.10523862 0.3756891 0.4985373 -0.020534959 0.129455259 0.20594357
#> 8 0.09707782 0.3676106 0.5174539 -0.017857642 -0.074201998 -0.08983281
#> 9 0.06836048 0.3299158 0.5918569 -0.009866868 -0.068360484 0.01697418
#> 10 0.05880602 0.3132481 0.6202558 -0.007690015 -0.058806016 -0.31324812
#> 11 0.03912356 0.2690653 0.6878484 -0.003962699 -0.039123555 -0.26906531
#> raw.rsd.3 se.0 se.1 se.2 se.3 std.rsd.0
#> 1 -0.14322104 0.397359953 0.46371351 0.47610220 0.35029812 2.0220663
#> 2 -0.20926492 0.150611412 0.19860274 0.21813376 0.18191928 3.1177497
#> 3 -0.24897378 0.078357401 0.11090564 0.12671381 0.11165000 2.9442258
#> 4 -0.27809653 0.035974863 0.05528201 0.06638675 0.06156999 0.3830354
#> 5 -0.10714402 0.019106171 0.03287157 0.04267975 0.04169091 -0.3169978
#> 6 -0.19432375 0.010996190 0.02128019 0.03036171 0.03072722 -0.1568583
#> 7 -0.31486387 0.014326112 0.03099761 0.04892172 0.05050741 -1.4333937
#> 8 0.18189246 0.007570744 0.01692484 0.02756294 0.02856568 -2.3587698
#> 9 0.06125317 0.004834464 0.01234350 0.02299737 0.02403956 -2.0409436
#> 10 0.37974416 0.010516294 0.02832213 0.05583668 0.05842604 -0.7312476
#> 11 0.31215156 0.003873963 0.01195570 0.02734578 0.02857270 -1.0229057
#> std.rsd.1 std.rsd.2 std.rsd.3
#> 1 -0.6749812 -0.7294006 -0.4088547
#> 2 0.6533110 -1.7881373 -1.1503175
#> 3 3.8103971 -3.1908333 -2.2299488
#> 4 1.0660662 3.0937290 -4.5167547
#> 5 3.8565422 -0.3179482 -2.5699613
#> 6 0.2811669 6.2600333 -6.3241558
#> 7 4.1762987 4.2096551 -6.2340132
#> 8 -4.3842081 -3.2591881 6.3675177
#> 9 -5.5381760 0.7380923 2.5480159
#> 10 -2.0763275 -5.6100775 6.4995706
#> 11 -3.2723764 -9.8393733 10.9248190