Bayesian Joint Latent Class and Regression Models.
R Package lcra
A user-friendly interface for doing joint Bayesian latent class and regression analysis with binary and continuous outcomes.
Simply specify the regression model and number of classes and lcra predicts class membership for each observation and accounts for uncertainty in class membership in the estimation of the regression parameters.
Why use this package?
This is the only package available for joint latent class and regression analysis. Other packages use a sequential procedure, where latent classes are determined prior to fitting the usual regression model. The only Bayesian alternative will require you to program the model by hand, which can be time consuming.
Overview
This R package provides a user-friendly interface for fitting Bayesian joint latent class and regression models. Using the standard R syntax, the user can specify the form of the regression model and the desired number of latent classes.
The technical details of the model implemented here are described in Elliott, Michael R., Zhao, Zhangchen, Mukherjee, Bhramar, Kanaya, Alka, Needham, Belinda L., “Methods to account for uncertainty in latent class assignments when using latent classes as predictors in regression models, with application to acculturation strategy measures” (2020) In press at Epidemiology.
Installation
JAGS is the new default Gibbs sampler for the package. Install JAGS here: JAGS Download.
This package uses the R interface for JAGS and WinBUGS. The package R2WinBUGS in turn depends on the standalone Windows program WinBUGS, and rjags depends on the standalone program JAGS. Follow this link: JAGS Download for JAGS download and installation instructions.
Once you’ve chosen between JAGS or WinBUGS, open R and run:
If the devtools package is not yet installed, install it first:
install.packages('devtools')
library(devtools)
# install lcra from Github:
install_github('umich-biostatistics/lcra')
library(lcra)
Example usage
Quick example:
inits = list(list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), tau = 0.5, true = rep(1, length = nrow(express))))
fit = lcra(formula = y ~ x1 + x2, family = "gaussian", data = express,
nclasses = 3, inits = inits, manifest = paste0("Z", 1:5),
n.chains = 1, n.iter = 500)
# use coda to analyze samples
library(coda)
summary(fit)
plot(fit)
NOTE: WinBUGS throws an error on Windows machines if you are not running as administrator. The error reads: Error in file(con, “wb”) : cannot open the connection.
Ignore the error. Once WinBUGS is finished drawing samples, follow the promp and return to R.
Model
The LCRA model is as follows: 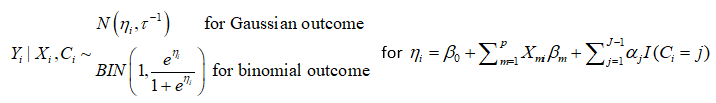
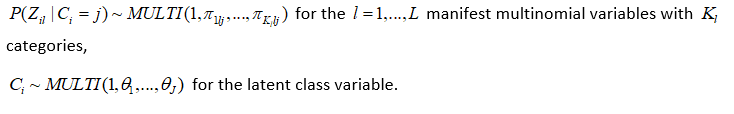
The following priors are the default and cannot be altered by the user:
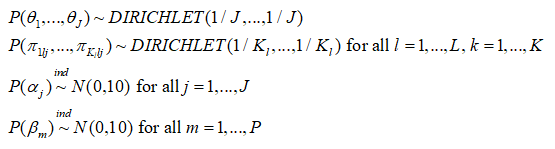

Please note also that the reference category for latent classes in the outcome model output is always the Jth latent class in the output, and the bugs output is defined by the Latin equivalent of the model parameters (beta, alpha, tau, pi, theta). Also, the bugs output includes the variable true, which corresponds to the MCMC draws of C_i, i = 1,…,n, as well as the MCMC draws of the deviance (DIC) statistic. Finally the bugs output for pi is stored in a three dimensional array corresponding to (class, variable, category), where category is indexed by 1 through maximum K_l; for variables where the number of categories is less than maximum K_l, these cells will be set to NA. The parameters outputed by the lcra function currently are not user definable.
More examples:
The main function for the joint model is lcra(). Use ?lcra for the R help file.
Here is an example analysis on simulated data with continuous and discrete outcomes:
# quick example
inits = list(list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), tau = 0.5, true = rep(1, length = nrow(express))))
fit = lcra(formula = y ~ x1 + x2, family = "gaussian", data = express,
nclasses = 3, inits = inits, manifest = paste0("Z", 1:5),
n.chains = 1, n.iter = 500)
data('paper_sim')
# Set initial values
inits =
list(
list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), tau = 0.5, true = rep(1, length = 100)),
list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), tau = 0.5, true = rep(1, length = 100)),
list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), tau = 0.5, true = rep(1, length = 100))
)
# Fit model 1
fit.gaus_paper = lcra(formula = Y ~ X1 + X2, family = "gaussian",
data = paper_sim, nclasses = 3, manifest = paste0("Z", 1:10),
inits = inits, n.chains = 3, n.iter = 5000)
# Model 1 results
library(coda)
summary(fit.gaus_paper)
plot(fit.gaus_paper)
# simulated examples
library(gtools) # for Dirichel distribution
# with binary response
n <- 500
X1 <- runif(n, 2, 8)
X2 <- rbinom(n, 1, .5)
Cstar <- rnorm(n, .25 * X1 - .75 * X2, 1)
C <- 1 * (Cstar <= .8) + 2 * ((Cstar > .8) & (Cstar <= 1.6)) + 3 * (Cstar > 1.6)
pi1 <- rdirichlet(10, c(5, 4, 3, 2, 1))
pi2 <- rdirichlet(10, c(1, 3, 5, 3, 1))
pi3 <- rdirichlet(10, c(1, 2, 3, 4, 5))
Z1<-(C==1)*t(rmultinom(n,1,pi1[1,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[1,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[1,]))%*%c(1:5)
Z2<-(C==1)*t(rmultinom(n,1,pi1[2,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[2,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[2,]))%*%c(1:5)
Z3<-(C==1)*t(rmultinom(n,1,pi1[3,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[3,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[3,]))%*%c(1:5)
Z4<-(C==1)*t(rmultinom(n,1,pi1[4,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[4,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[4,]))%*%c(1:5)
Z5<-(C==1)*t(rmultinom(n,1,pi1[5,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[5,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[5,]))%*%c(1:5)
Z6<-(C==1)*t(rmultinom(n,1,pi1[6,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[6,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[6,]))%*%c(1:5)
Z7<-(C==1)*t(rmultinom(n,1,pi1[7,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[7,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[7,]))%*%c(1:5)
Z8<-(C==1)*t(rmultinom(n,1,pi1[8,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[8,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[8,]))%*%c(1:5)
Z9<-(C==1)*t(rmultinom(n,1,pi1[9,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[9,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[9,]))%*%c(1:5)
Z10<-(C==1)*t(rmultinom(n,1,pi1[10,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[10,]))%*%c(1:5)+(C==3)*t(rmultinom(n,1,pi3[10,]))%*%c(1:5)
Z <- cbind(Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8, Z9, Z10)
Y <- rbinom(n, 1, exp(-1 - .1*X1 + X2 + 2*(C == 1) + 1*(C == 2)) /
(1 + exp(1 - .1*X1 + X2 + 2*(C == 1) + 1*(C == 2))))
mydata = data.frame(Y, X1, X2, Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8, Z9, Z10)
inits = list(list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), true = rep(1, length = nrow(mydata))))
fit = lcra(formula = Y ~ X1 + X2, family = "binomial", data = mydata,
nclasses = 3, inits = inits, manifest = paste0("Z", 1:10),
n.chains = 1, n.iter = 1000)
summary(fit)
plot(fit)
# with continuous response
n <- 500
X1 <- runif(n, 2, 8)
X2 <- rbinom(n, 1, .5)
Cstar <- rnorm(n, .25*X1 - .75*X2, 1)
C <- 1 * (Cstar <= .8) + 2*((Cstar > .8) & (Cstar <= 1.6)) + 3*(Cstar > 1.6)
pi1 <- rdirichlet(10, c(5, 4, 3, 2, 1))
pi2 <- rdirichlet(10, c(1, 3, 5, 3, 1))
pi3 <- rdirichlet(10, c(1, 2, 3, 4, 5))
pi4 <- rdirichlet(10, c(1, 1, 1, 1, 1))
Z1<-(C==1)*t(rmultinom(n,1,pi1[1,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[1,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[1,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[1,]))%*%c(1:5)
Z2<-(C==1)*t(rmultinom(n,1,pi1[2,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[2,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[2,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[2,]))%*%c(1:5)
Z3<-(C==1)*t(rmultinom(n,1,pi1[3,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[3,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[3,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[3,]))%*%c(1:5)
Z4<-(C==1)*t(rmultinom(n,1,pi1[4,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[4,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[4,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[4,]))%*%c(1:5)
Z5<-(C==1)*t(rmultinom(n,1,pi1[5,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[5,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[5,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[5,]))%*%c(1:5)
Z6<-(C==1)*t(rmultinom(n,1,pi1[6,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[6,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[6,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[6,]))%*%c(1:5)
Z7<-(C==1)*t(rmultinom(n,1,pi1[7,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[7,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[7,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[7,]))%*%c(1:5)
Z8<-(C==1)*t(rmultinom(n,1,pi1[8,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[8,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[8,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[8,]))%*%c(1:5)
Z9<-(C==1)*t(rmultinom(n,1,pi1[9,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[9,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[9,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[9,]))%*%c(1:5)
Z10<-(C==1)*t(rmultinom(n,1,pi1[10,]))%*%c(1:5)+(C==2)*
t(rmultinom(n,1,pi2[10,]))%*%c(1:5)+(C==3)*
t(rmultinom(n,1,pi3[10,]))%*%c(1:5)+(C==4)*t(rmultinom(n,1,pi4[10,]))%*%c(1:5)
Z <- cbind(Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8, Z9, Z10)
Y <- rnorm(n, 10 - .5*X1 + 2*X2 + 2*(C == 1) + 1*(C == 2), 1)
mydata = data.frame(Y, X1, X2, Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8, Z9, Z10)
inits = list(list(theta = c(0.33, 0.33, 0.34), beta = rep(0, length = 3),
alpha = rep(0, length = 2), true = rep(1, length = nrow(mydata)),
tau = 0.5))
fit = lcra(formula = Y ~ X1 + X2, family = "gaussian", data = mydata,
nclasses = 3, inits = inits, manifest = paste0("Z", 1:10),
n.chains = 1, n.iter = 1000)
summary(fit)
plot(fit)
Current Suggested Citation
“Methods to account for uncertainty in latent class assignments when using latent classes as predictors in regression models, with application to acculturation strategy measures” (2020) In press at Epidemiology.