Description
'MADGRAD' Method for Stochastic Optimization.
Description
A Momentumized, Adaptive, Dual Averaged Gradient Method for Stochastic Optimization algorithm. MADGRAD is a 'best-of-both-worlds' optimizer with the generalization performance of stochastic gradient descent and at least as fast convergence as that of Adam, often faster. A drop-in optim_madgrad() implementation is provided based on Defazio et al (2020) <arxiv:2101.11075>.
README.md
madgrad
The Madgrad package is an R port of the original madgrad by Aaron Defazio and Samy Jelassi. See the Arxiv paper for details on the method.
Installation
Madgrad is not yet on CRAN. The development version from GitHub can be installed with:
# install.packages("devtools")
devtools::install_github("mlverse/madgrad")
Example
This is a small example showing how to use madgrad with torch to minimize a function, of course, madgrad is not the best algorithm for this task and should work better for neural network training.
library(madgrad)
library(torch)
torch_manual_seed(1)
f <- function(x, y) {
log((1.5 - x + x*y)^2 + (2.25 - x - x*(y^2))^2 + (2.625 - x + x*(y^3))^2)
}
x <- torch_tensor(-5, requires_grad = TRUE)
y <- torch_tensor(-2, requires_grad = TRUE)
opt <- optim_madgrad(params = list(x, y), lr = 0.1)
for (i in 1:100) {
opt$zero_grad()
z <- f(x, y)
z$backward()
opt$step()
}
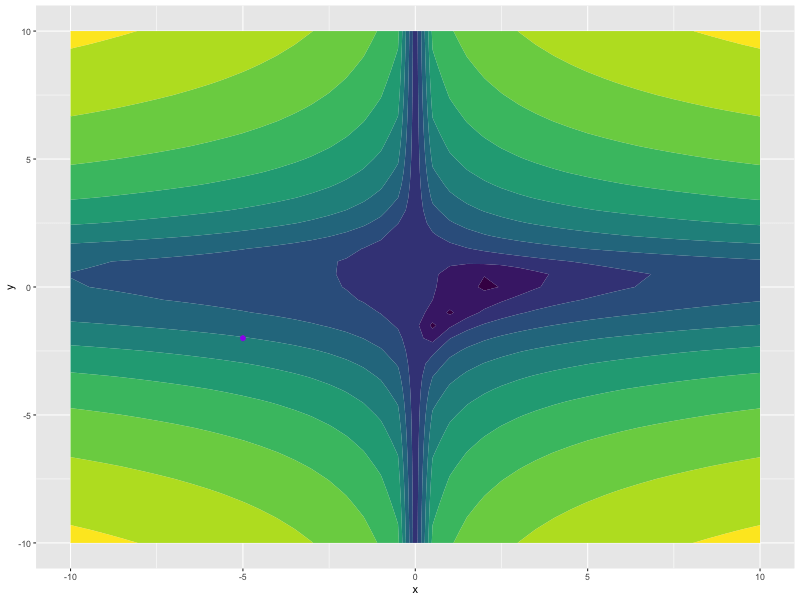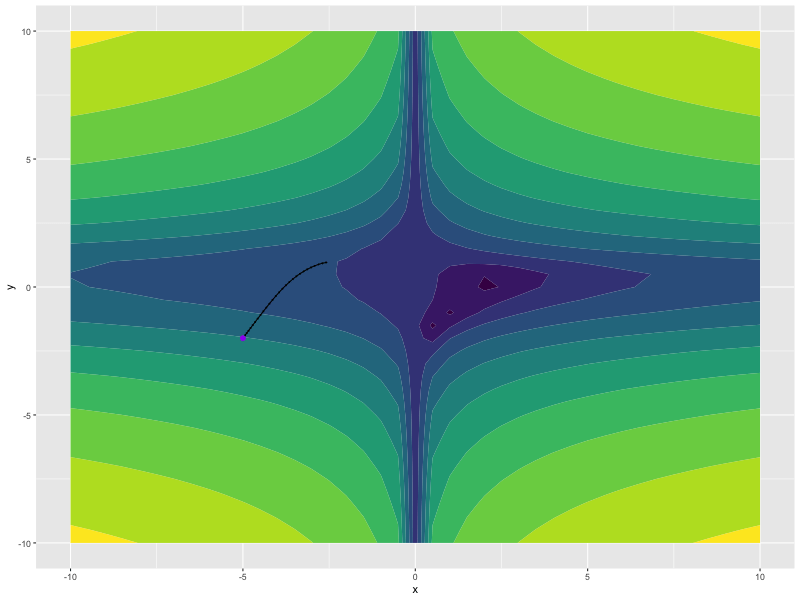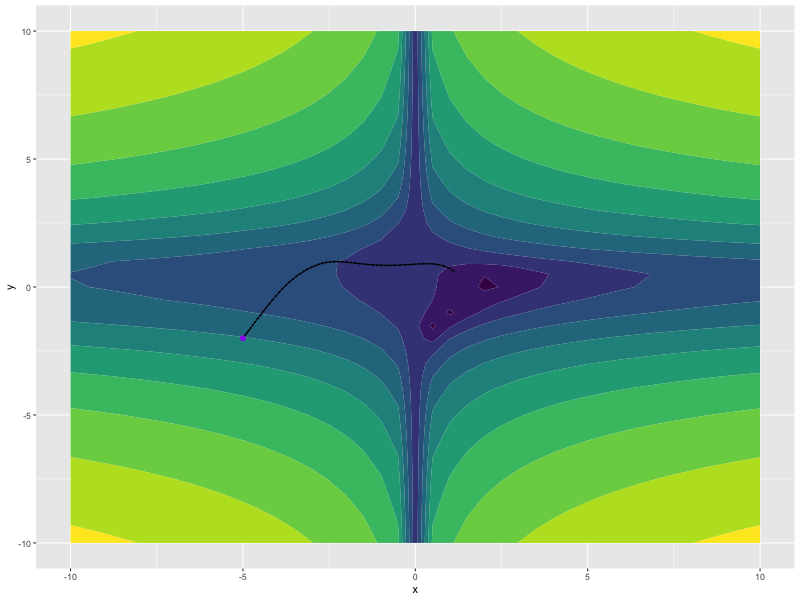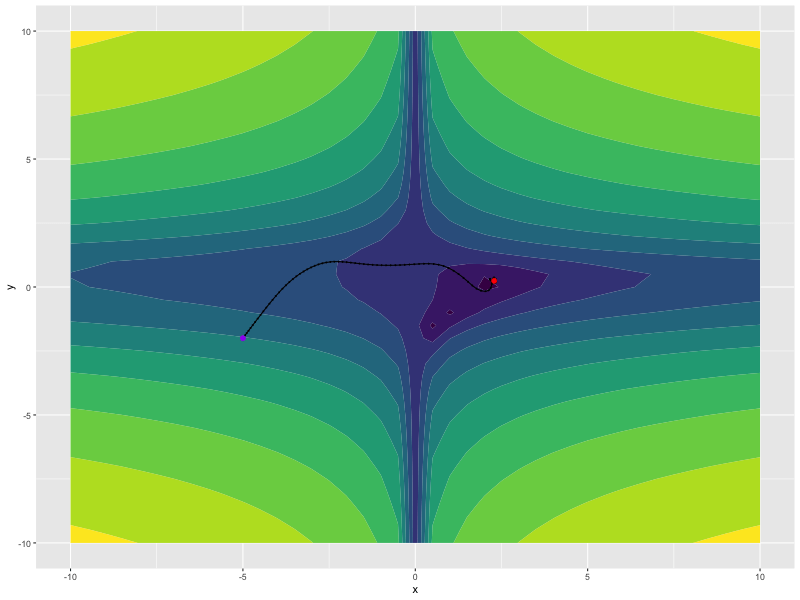
x
#> torch_tensor
#> 2.2882
#> [ CPUFloatType{1} ]
y
#> torch_tensor
#> 0.2412
#> [ CPUFloatType{1} ]