Monte Carlo Statistical Simulation Tools Using a Functional Approach.

mcstatsim package

About

The mcstatsim package offers an efficient, functional programming-based approach for statistical simulations, centralizing the process in a single higher-order function for better manageability. Besides, it includes ready-to-use functions for well-known simulation targets.

How?

The core runsim() function processes simulation parameters via expanded grid, mapping them to the simulation function.

Outputs are deliberately structured as dataframe to simplify analysis and visualization, addressing the limitations of list outputs in data manipulation.

Installation

You can install the latest development version of mcstatsim from gitHub:

# install.packages("devtools")
#devtools::install_github("ielbadisy/mcstatsim")

Usage

Here is a basic example to get you started with mcstatsim:

library(mcstatsim)

# Define a simple simulation function
sim_function <- function(a, b) {
  Sys.sleep(0.5)  # Simulate a time-consuming process
  return(data.frame(result = a + b))
  }

# Generate a grid of parameters
params <- expand.grid(a = 1:3, b = 4:6)

# Run simulations
results <- runsim(n = 3, grid_params = params, sim_func = sim_function, show_progress = TRUE)

This example demonstrates how to define a simple simulation function, create a grid of parameters for the simulation, and run the simulations in parallel using mcstatsim.

Working example (more detailed)

To illustrate the utility of this package in a concrete example, we will simulate the evaluation of several imputation methods to assess their effectiveness in preserving the accuracy of coefficient estimates in a Cox regression model. This will demonstrate the creation of a simulation function, setting up parameters, and using mcstatsim to run these simulations in parallel.

Simulation aim: We will to assess the performance of some imputation methods regarding their capacity to preserve the values of coefficients estimates. For this aim, we well set up the following simulation design:

1. Generate fully observed data -> data_complete

2. estimate the beta coefficients values from data_complete

3. Introduce missigness under MCAR to complete dataset generated in (1) -> data_missing

4. impute the dataset generated at (3) -> data_imputed

5. Use the following simulation targets to compute the distortion between $\beta_{true}$ from data_complete and $\beta_i$ from data_imputed:

• Bias: Bias measures the average deviation of the estimated coefficients from the true coefficients.

$$ \text{Bias}(\hat{\beta}) = E[\hat{\beta}] - \beta_{\text{true}} $$

• Coverage: Coverage is the proportion of times the true coefficient value falls within the estimated confidence interval across all simulations.

$$ \text{Coverage} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{1}(\beta_{\text{true}} \in \text{CI}_i) $$

• Mean Squared Error (MSE): MSE combines both the variance of the estimator and its bias, providing a single measure of estimation quality.

$$ \text{MSE} = E[(\hat{\beta} - \beta_{\text{true}})^2] $$

NB: All these metrics (and more) are already implemented in the mcstatsim package (see ?calc_bias(), ?calc_coverage(), and ?calc_rmse().

Step 1: Define the helpers

Since we want to preserve the spirit of the functional prgramming style, all our simulation design step will be decomposed as helper functions. In others words, the simulation steps will be translated to functions as follow:

pacman::p_load(mcstatsim, survival, dplyr, ggplot2)

## (1) generate fully observed data -> `data_complete`
gencox <- function(n = 300, maxTime = 7, logHR = 0.5) {
  lambda <- 0.1
  rho <- 1.6
  rateC <- 0.09

  # covariates
  x1 <- rnorm(n)
  x2 <- x1^2 + x1 + runif(n)
  x3 <- rbinom(n, 1, 0.5)

  # estimated survival times
  U <- runif(n)
  Tlat <- (-log(U) / (lambda * exp(logHR * (x1 + x2 + x3))))^(1 / rho)
  Ctimes <- rexp(n, rate = rateC)

  # follow-up times and event indicators
  time <- pmin(Tlat, Ctimes)
  status <- as.numeric(Tlat <= Ctimes)
  time <- ifelse(time > maxTime, maxTime, time)
  status <- ifelse(time >= maxTime, 1, status)
  
  data <- data.frame(time, status, x1, x2, x3)
  data$x3 <- as.factor(data$x3)
  
  return(data)
  }

## (2) estimate the beta coefficients values from `data_complete`
estimate_coxest <- function(data) {
  myFormula <- survival::Surv(time, status) ~ x1 + x2 + x3
  coefs <- summary(survival::coxph(myFormula, data = data))$coef
  coefs[, 1]
}

## (3) introduce missigness under MCAR to complete dataset generated in (1) -> `data_missing`
introduce_MCAR <- function(x, covariates = names(x), p = 0.3) {
  
  stopifnot(is.data.frame(x), p >= 0 && p <= 1, all(covariates %in% names(x)))
  x[covariates] <- lapply(x[covariates], function(z) {
    z[sample(length(z), floor(p * length(z)))] <- NA
    z
  })
  
  return(x)
}

## (4) impute the dataset generated at (3) -> `data_imputed`
imputer <- function(data, method) {
  stopifnot(is.data.frame(data))
  if (is.factor(method)) {method <- as.character(method)}

  supported_methods <- c("knn", "cart", "missforest", "missranger", "misscforest", "complete")
  stopifnot(method %in% supported_methods)
  
  data_imputed <- switch(method,
                 knn = VIM::kNN(data)[names(data)],
                 cart = simputation::impute_cart(data, .~.),
                 missforest = missForest::missForest(data, xtrue = data, verbose = FALSE)$ximp,
                 missranger = missRanger::missRanger(data, pmm.k = 5, num.trees = 100, verbose = 0),
                 misscforest = suppressWarnings(missCforest::missCforest(data, ntree = 10L)),
                 complete = data[stats::complete.cases(data), ])
  
  return(data_imputed)
  }

## (5) compute the simulation targets
evaluate_coxest <- function(data, truelogHR) {
  myFormula <- survival::Surv(time, status) ~ x1 + x2 + x3
  coefs <- summary(survival::coxph(myFormula, data = data))$coef
  estimates <- as.data.frame(coefs)
  
  out <- data.frame(
    estimates = estimates$coef,
    ci_lower = estimates$coef - 1.96 * estimates$`se(coef)`,
    ci_upper = estimates$coef + 1.96 * estimates$`se(coef)`
    )
  
  out$bias <- mcstatsim::calc_bias(out$estimates, truelogHR)$bias
  out$coverage <- mcstatsim::calc_coverage(out$ci_lower, out$ci_upper, truelogHR)$coverage
  out$rmse <- mcstatsim::calc_rmse(out$estimates, truelogHR)$rmse
  
  return(out)
  }

Step 2: Define the simulation function

simcox <- function(n, logHR, pmiss, covariates = c("x2"), method = method){
  data_complete <- gencox(n = n)
  truelogHR <- estimate_coxest(data_complete)
  data_missing <- introduce_MCAR(data_complete, covariates = covariates, p = pmiss)
  data_imputed <- imputer(data_missing, method = method)
  res_est <- evaluate_coxest(data_missing, truelogHR = truelogHR)
  res <- cbind(n, pmiss, method, covariates, res_est, row.names = NULL)
  return(res)
  }

Step 3: define the parameters of the simulation

Now, to link our simulation function to the simulation parameters, we will generate a grid of paremeters with the same names as the argument of simulation function:

params <- expand.grid(n = c(200, 500), 
                      logHR = 0.5,
                      pmiss = c(0.2, 0.5),
                      method = c("knn", "cart", "missforest", "missranger",
                                 "misscforest", "complete"))

Step 4: Run the simulation

In one line of code, we can lunch our simulation:

set.seed(123)
sim_res <- runsim(n = 100, grid_params = params, sim_func = simcox, show_progress = FALSE, num_cores = 6)

Step 5: summerize the results

Finaly, we retreive all the results in one single dataset (i.e sim_res) for ploting and table production:

sim_res$bias <- abs(sim_res$bias)

sim_res2 <- gather(sim_res, metric, value, c(bias, rmse))
ggplot(sim_res2, aes(x=value, y=method, fill=method)) +
  stat_summary(fun=mean, geom="point", shape=20, size=3, color="red") + 
  theme_bw() +
  theme(axis.text.x = element_text(hjust = 1),
        legend.position = "none") +
  labs(x = "", y = "") +
  facet_grid(pmiss~metric, scales="free")

ggsave("quick_res.png")

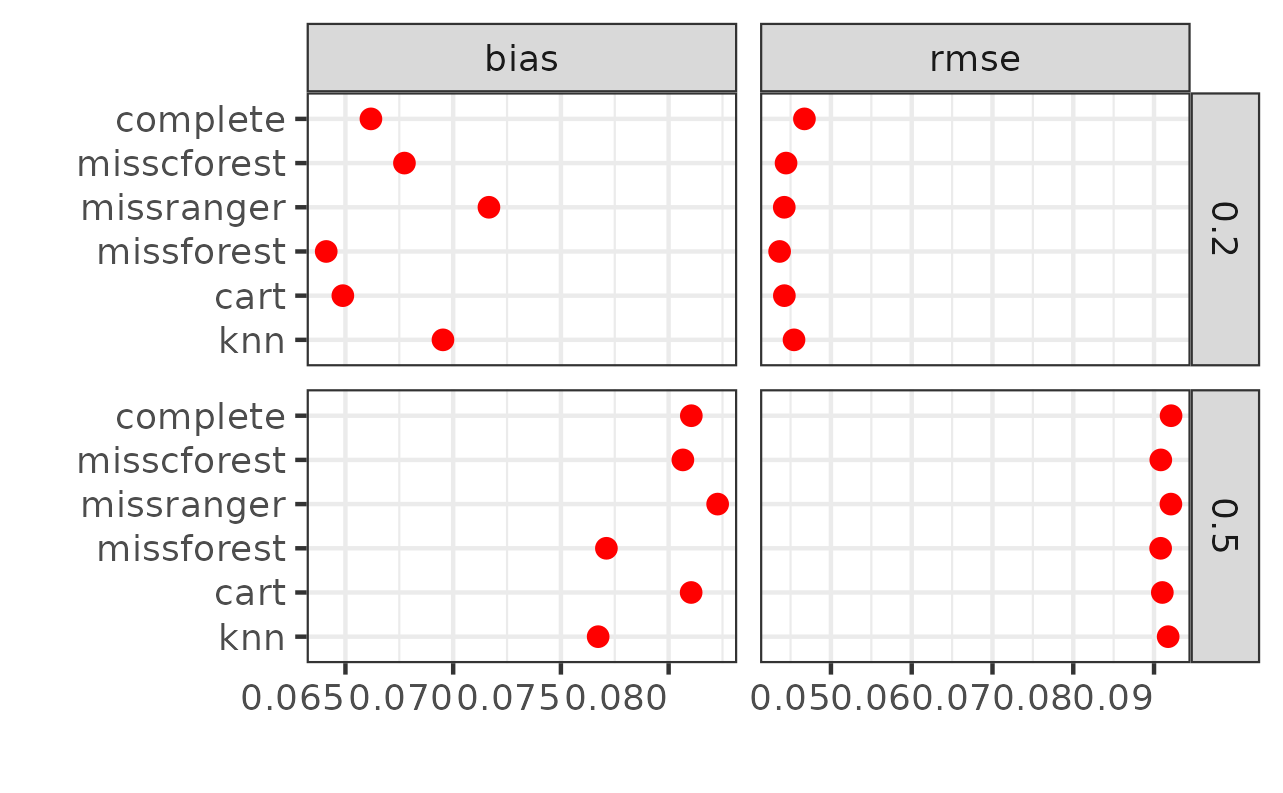
Let’s skip interpreting the results since the simulation design isn’t complete yet—we need to add more simulation targets and assess different hyperparameter values. However, this provides a good demonstration of how the mcstatsim package can efficiently organize Monte Carlo simulations without the complexities of for-loops and managing numerous parameters.

Features

• Functional programming approach: Streamlines the process of setting up and running simulations.

• Parallel execution: Leverages parallel computing to speed up the execution of simulations.

• Structured output: Returns simulation results in a dataframe, facilitating quick analysis and visualization.

Summary of Changes in Version 0.5.0

The major improvement in version 0.5.0 compared to version 0.1.0 is the integration of parallel computing support using the future package backend within the pbapply package. This enhancement overcomes the previous limitation, which only supported multicore parallel computing on Unix-based operating systems through parallel::mcmapply(). With this update, mcstatsim now supports parallel computing across various operating systems, including Windows, thereby providing greater flexibility and performance improvements for users.

Contributing

Contributions are welcome! If you’d like to help improve mcstatsim, please feel free to submit a pull request.