Multiple Imputation in Cluster Analysis.
miclust
This package performs cluster analysis with selection of the final number of clusters and an optional variable selection procedure. The package is designed to integrate the results of multiple imputation to deal with missing raw data while accounting for the uncertainty that such imputations introduce in the final results.
Getting started
The last version released on CRAN can be installed within an R session by executing:
install.packages("miclust")
Once the package has been installed, a summary of the main functions is available using the help function:
library(miclust)
#>
#> This is miclust 1.2.6. For details, use:
#> > help(package = 'miclust')
#>
#> To cite the methods in the package use:
#> > citation('miclust')
help(miclust)
Example
Data
Data minhanes is a list with 101 data sets. The first data set contains nhanesdata from the mice package. The remaining data sets were obtained by applying the multiple imputation function mice, from the same package. The first step of the analysis is to apply the getdata function to minhanes, resulting in minhanes1, a list with two objects: rawdata, a data.frame containing the raw data, and impdata, a list containing the imputed data sets. getdata standardizes all variables, so categorical variables need to have numeric values. Standardization is performed by centering all variables at the mean and then dividing by the standard deviation (or the difference between the maximum and the minimum values for binary variables). Such a standardization is applied only to the imputed data sets, except in the case of analyzing just the raw data (i.e. complete cases analysis), in which raw data are also internally standardized.
library(miclust)
data(minhanes)
### data preparation:
minhanes1 <- getdata(data = minhanes)
class(minhanes1)
#> [1] "list" "midata"
### raw data:
minhanes1$rawdata
#> age bmi hyp chl
#> 1 1 NA NA NA
#> 2 2 22.7 1 187
#> 3 1 NA 1 187
#> 4 3 NA NA NA
#> 5 1 20.4 1 113
#> 6 3 NA NA 184
#> 7 1 22.5 1 118
#> 8 1 30.1 1 187
#> 9 2 22.0 1 238
#> 10 2 NA NA NA
#> 11 1 NA NA NA
#> 12 2 NA NA NA
#> 13 3 21.7 1 206
#> 14 2 28.7 2 204
#> 15 1 29.6 1 NA
#> 16 1 NA NA NA
#> 17 3 27.2 2 284
#> 18 2 26.3 2 199
#> 19 1 35.3 1 218
#> 20 3 25.5 2 NA
#> 21 1 NA NA NA
#> 22 1 33.2 1 229
#> 23 1 27.5 1 131
#> 24 3 24.9 1 NA
#> 25 2 27.4 1 186
### first (standardized) imputed data set:
minhanes1$impdata[[1]]
#> age bmi hyp chl
#> 1 -0.9149325 2.0012331 -0.24 -0.1489984
#> 2 0.2889260 -0.9445072 -0.24 -0.1227663
#> 3 -0.9149325 0.4582263 -0.24 -0.1227663
#> 4 1.4927846 -0.2898982 0.76 0.6904293
#> 5 -0.9149325 -1.4822217 -0.24 -2.0639429
#> 6 1.4927846 0.1776796 0.76 -0.2014626
#> 7 -0.9149325 -0.9912650 -0.24 -1.9327823
#> 8 -0.9149325 0.7855307 -0.24 -0.1227663
#> 9 0.2889260 -1.1081594 -0.24 1.2150716
#> 10 0.2889260 -1.4822217 -0.24 -0.1227663
#> 11 -0.9149325 0.6686363 -0.24 0.9789826
#> 12 0.2889260 0.1543007 -0.24 0.3756439
#> 13 1.4927846 -1.1782961 -0.24 0.3756439
#> 14 0.2889260 0.4582263 0.76 0.3231797
#> 15 -0.9149325 0.6686363 -0.24 -0.1227663
#> 16 -0.9149325 0.4582263 -0.24 -0.1227663
#> 17 1.4927846 0.1075429 0.76 2.4217489
#> 18 0.2889260 -0.1028671 0.76 0.1920191
#> 19 -0.9149325 2.0012331 -0.24 0.6904293
#> 20 1.4927846 -0.2898982 0.76 -0.1489984
#> 21 -0.9149325 -1.4822217 -0.24 -1.5917648
#> 22 -0.9149325 1.5102763 -0.24 0.9789826
#> 23 -0.9149325 0.1776796 -0.24 -1.5917648
#> 24 1.4927846 -0.4301716 -0.24 0.3231797
#> 25 0.2889260 0.1543007 -0.24 -0.1489984
Analysis
Multiple imputation clustering process with backward variable selection:
### using only the imputations 1 to 50 for the clustering process and exploring
### 2 vs. 3 clusters:
minhanes1clust <- miclust(data = minhanes1, search = "backward", ks = 2:3, usedimp = 1:50, seed = 4321)
#> ....imp 5....imp 10....imp 15....imp 20....imp 25....imp 30....imp 35....imp 40....imp 45....imp 50
#>
#> Analysis done.
minhanes1clust
#>
#> Results using 50 imputations:
#> ------------------------------------------------
#>
#> k=V1 k=V2
#> Frequency of selection (%) 56.00 44.00
#> Median number of selected variables 1.0 2.0
### optimal number of clusters
minhanes1clust$kfin
#> [1] 2
Selection frequency of the variables for the optimal number of clusters:
y <- getvariablesfrequency(minhanes1clust)
y
#> $percfreq
#> [1] 100 4 2 2
#>
#> $varnames
#> [1] "hyp" "age" "bmi" "chl"
plot(y$percfreq, type = "h", main = "", xlab = "Variable", ylab = "Percentage of times selected",
xlim = 0.5 + c(0, length(y$varnames)), lwd = 5, col = "blue", xaxt = "n")
axis(1, at = 1:length(y$varnames), labels = y$varnames)
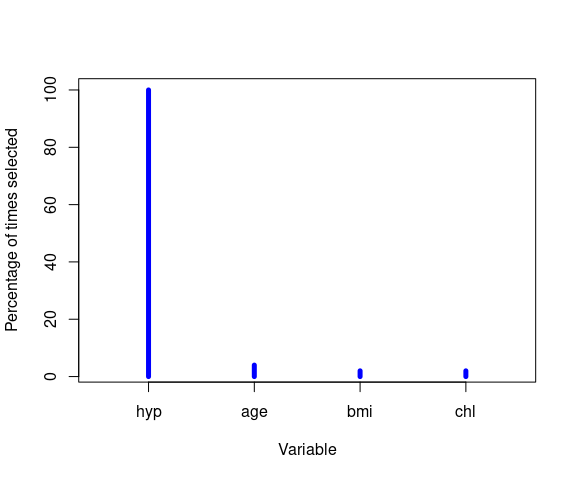
Graphical representation of the results:
plot(minhanes1clust)
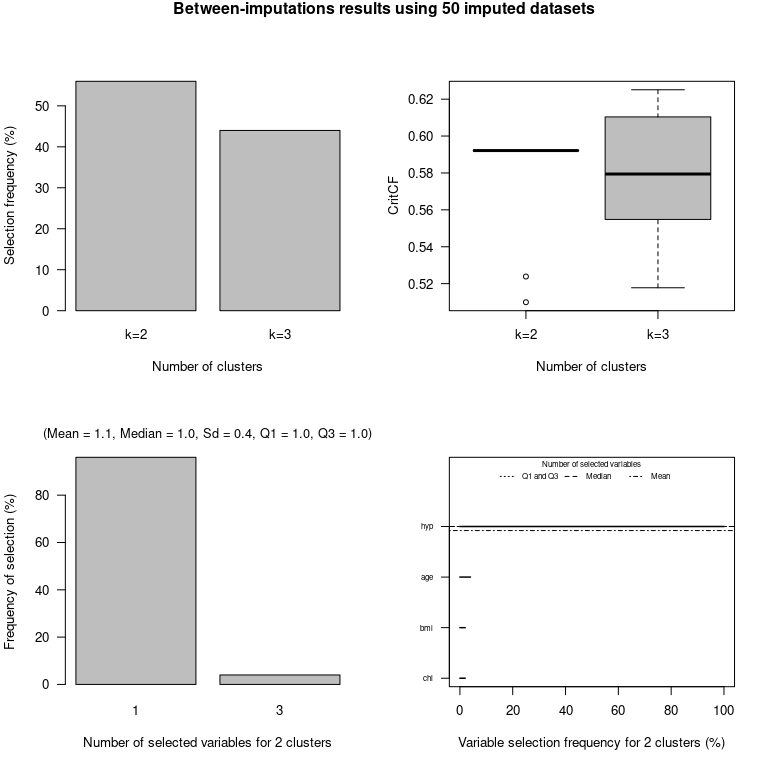
Default summary for the optimal number of clusters:
summary(minhanes1clust)
#> Warning in summary.miclust(minhanes1clust): 'quantilevars' not provided. Setting it to 0.5.
#>
#> Results using:
#> 50 imputed data sets for the cluster analysis
#> 100 imputed data sets for the descriptive summary
#> 2 as the final number of clusters
#> -----------------------------------------------------------
#>
#> Presence of the variables in the subset of selected variables:
#> Variable Presence(%)
#> 1 hyp 100
#> 2 age 4
#> 3 bmi 2
#> 4 chl 2
#>
#> Selected variables:
#> [1] "hyp"
#>
#> Cohen's kappa between-imputations distribution (99 comparisons):
#> 2.5% 25% 50% mean 75% 97.5%
#> 0.48 0.65 0.78 0.75 0.88 1.00
#>
#> Between-imputation clusters size distribution (100 imputations):
#> size min. 2.5% 25% 50% mean 75% 97.5% max.
#> cluster 1 7 4 4 6 7 6.5 7 9 10
#> cluster 2 18 15 16 18 18 18.5 19 21 21
#>
#> Probability of assignment to the cluster distribution (100 imputations):
#> min Q1 Q2 Q3 max
#> Assigned to cluster 1 0.51 0.54 1 1 1
#> Assigned to cluster 2 0.52 0.93 1 1 1
#>
#> Within-cluster summary (100 imputations):
#> %miss. %miss.(cl.1) %miss.(cl.2) mean (cl.1) sd (cl.1) mean (cl.2)
#> hyp 0 0 0 2 0 1
#> sd (cl.2)
#> hyp 0
Summary forcing 3 clusters:
summary(minhanes1clust, k = 3)
#> Warning in summary.miclust(minhanes1clust, k = 3): 'quantilevars' not provided. Setting it to 0.5.
#>
#> Results using:
#> 50 imputed data sets for the cluster analysis
#> 100 imputed data sets for the descriptive summary
#> 3 as the final number of clusters
#> -----------------------------------------------------------
#>
#> Presence of the variables in the subset of selected variables:
#> Variable Presence(%)
#> 1 hyp 96
#> 2 age 94
#> 3 bmi 46
#> 4 chl 30
#>
#> Selected variables:
#> [1] "hyp" "age"
#>
#> Cohen's kappa between-imputations distribution (99 comparisons):
#> 2.5% 25% 50% mean 75% 97.5%
#> 1 1 1 1 1 1
#>
#> Between-imputation clusters size distribution (100 imputations):
#> size min. 2.5% 25% 50% mean 75% 97.5% max.
#> cluster 1 12 12 12 12 12 12 12 12 12
#> cluster 2 7 7 7 7 7 7 7 7 7
#> cluster 3 6 6 6 6 6 6 6 6 6
#>
#> Probability of assignment to the cluster distribution (100 imputations):
#> min Q1 Q2 Q3 max
#> Assigned to cluster 1 1 1 1 1 1
#> Assigned to cluster 2 1 1 1 1 1
#> Assigned to cluster 3 1 1 1 1 1
#>
#> Within-cluster summary (100 imputations):
#> %miss. %miss.(cl.1) %miss.(cl.2) %miss.(cl.3) mean (cl.1) sd (cl.1)
#> hyp.mean 0 0 0 0 1 0
#> age.mean 0 0 0 0 1 0
#> mean (cl.2) sd (cl.2) mean (cl.3) sd (cl.3)
#> hyp.mean 1.4 0.55 1.5 0.58
#> age.mean 2.0 0.00 3.0 0.00
References
The methodology used in the package is described in
- Basagaña X, Barrera-Gómez J, Benet M, Antó JM, Garcia-Aymerich J. A Framework for Multiple Imputation in Cluster Analysis. American Journal of Epidemiology. 2013;177(7):718-725. https://doi.org/10.1093/aje/kws289