Multi-Level Model Assessment Kit.

mlmtools

Multilevel and mixed effects models often require specialized data pre-processing and further post-estimation derivations and graphics to gain insight into model results. mlmtools is a suite of pre- and post-estimation tools for multilevel models in R. The package’s post-estimation tools are designed to work with models estimated using lme4’s lmer function, which fits linear mixed effects regression models. Although nearly all the functions provided in the mlmtools package exist as singleton functions within other R packages, they are often improved in mlmtools and more accessible by being located within a multilevel modeling specific package.

The package was developed by Laura Jamison, Jessican Mazen, Erik Ruzek, and Gus Sjobek.

Included functions

• Center level-1 predictors around their group (cluster) means
• Intraclass correlation coefficients (ICC)
• Variance explained
  • When comparing nested models
  • 
• Visualizations
  • Associations between variables within clusters
  • Associations between variables between clusters
  • Caterpillar plots
• Test model assumptions

Installation

To install the latest release version (1.0.0) from GitHub with:

# install.packages("devtools")
devtools::install_github("lj5yn/mlmtools")

Sample workflow

Working with the included data, we briefly show how some of the included functions can be used.

# data
library(mlmtools)
library(lme4)
#> Loading required package: Matrix
data("instruction")

# fit variance components model
fit1 <- lmer(mathgain ~ 1 + (1|classid), instruction)
  
# intraclass correlation coefficient
ICCm(fit1)
#> Likeness of mathgain values of units in the same classid factor: 0.149

# group-mean center mathkind 
center(instruction, x="mathkind", grouping = "classid")
#> The following variables (deviation, group summary) were added to the dataset: 
#>  classid_mathkind.devcmn classid_mathkind.cmn 
#> See mlmtools documentation for detailed description of variables added.

# add group-mean centered and group mean as predictors
fit2 <- lmer(mathgain ~ classid_mathkind.devcmn + classid_mathkind.cmn + (1|classid), instruction)

# variance explained by adding predictor
varCompare(fit2, fit1)
#> fit2 explains 31.08% more variance than fit1

# test model assumptions
mlm_assumptions(fit2)
#> Homogeneity of variance assumption met.
#> 
#> Model contains fewer than 2 terms, multicollinearity cannot be assessed.
#> 
#> No outliers detected.
#> 
#> Visually inspect all 4 plot types by calling them from the object created by mlm_assumptions() such as object$fitted.residual.plot and object$resid.normality.plot. linearity.plots and resid.component.plots may contain more than one plot depending on the model specified. Check how many there are, for example using length(object$linearity.plots). Then inspect each plot within each object, for example using object$linearity.plots[[1]] to access the first plot within the linearity.plots list.
#> 
#> See ?mlm_assumptions for more details and resources.
#> 
#> $linearity.plots
#> $linearity.plots[[1]]

#> 
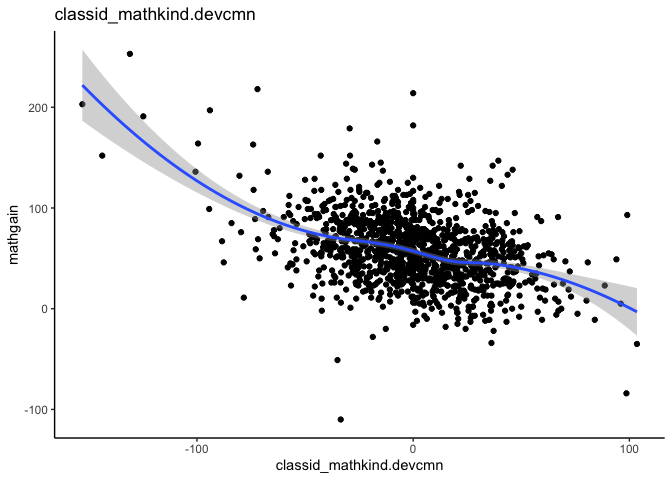
#> $linearity.plots[[2]]

#> 
#> 
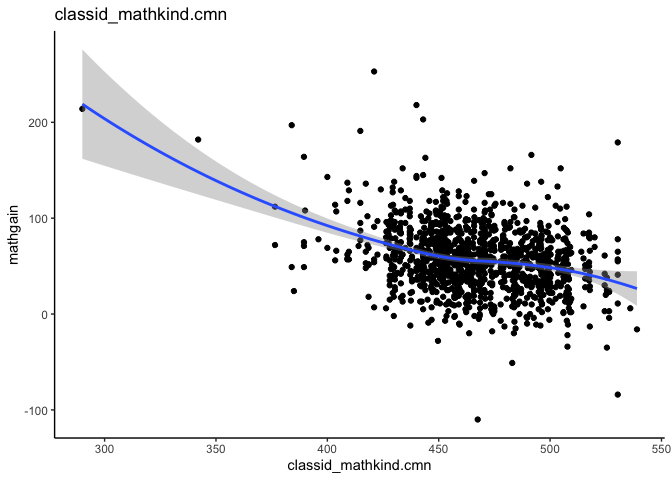
#> $homo.test
#> Analysis of Variance Table
#> 
#> Response: model.Res2
#>             Df     Sum Sq Mean Sq F value  Pr(>F)  
#> classid      1    6872688 6872688  3.4323 0.06418 .
#> Residuals 1188 2378796930 2002354                  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> $fitted.residual.plot

#> 
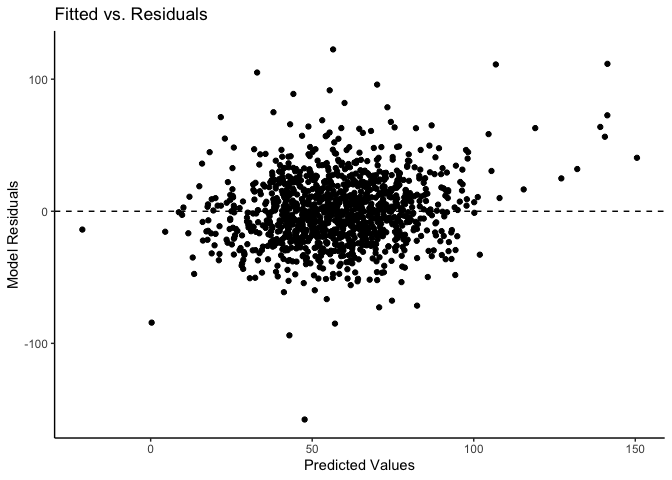
#> $outliers
#> [1] "664"
#> 
#> $resid.normality.plot

#> 
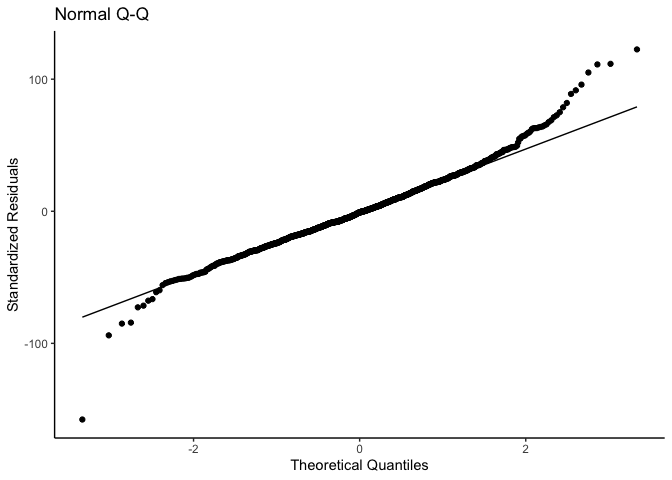
#> $resid.component.plots
#> $resid.component.plots[[1]]
#> `geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'

#> 
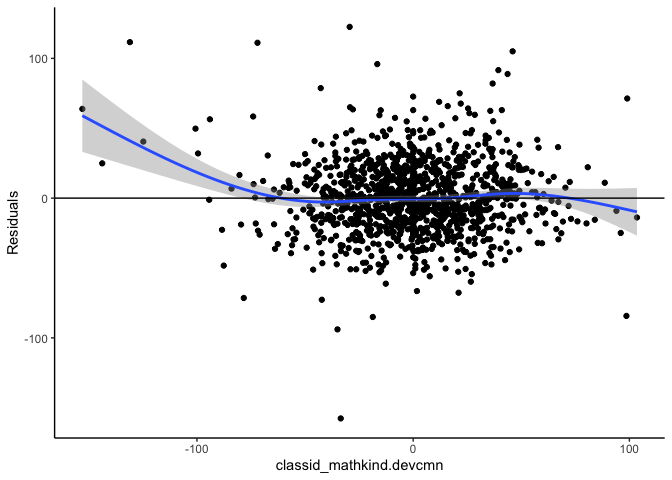
#> $resid.component.plots[[2]]
#> `geom_smooth()` using method = 'gam' and formula 'y ~ s(x, bs = "cs")'

#> 
#> 
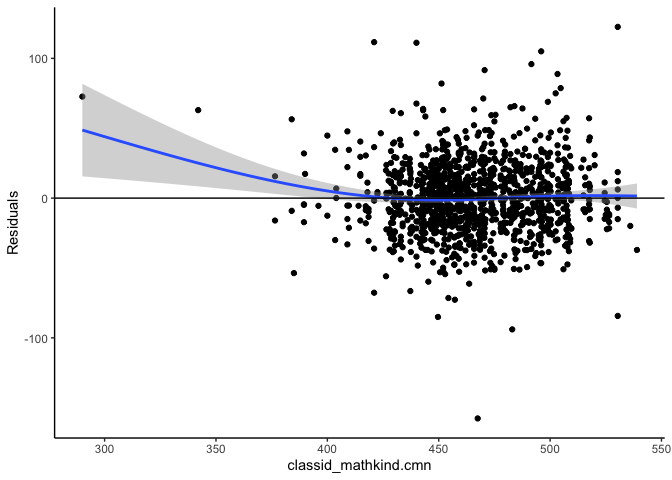
#> $multicollinearity
#> [1] "Model contains fewer than 2 terms, multicollinearity cannot be assessed.\n"
#> 
#> attr(,"class")
#> [1] "mlm_assumptions"

# variance explained by the model
rsqmlm(fit2)
#> 24.58% of the total variance is explained by the fixed effects.
#> 37.73% of the total variance is explained by both fixed and random effects.

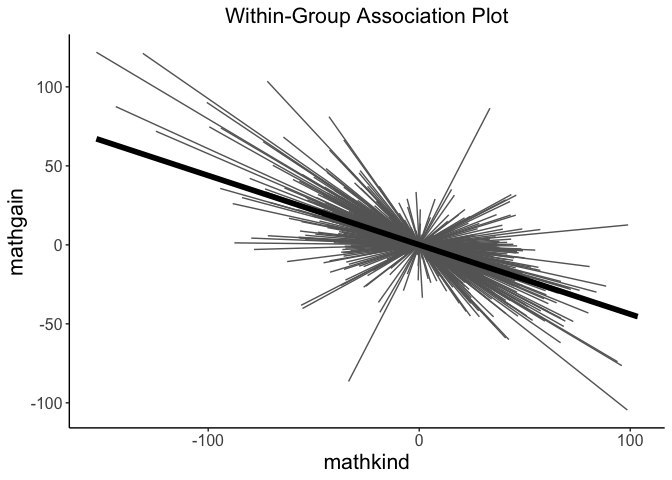
Visualizations

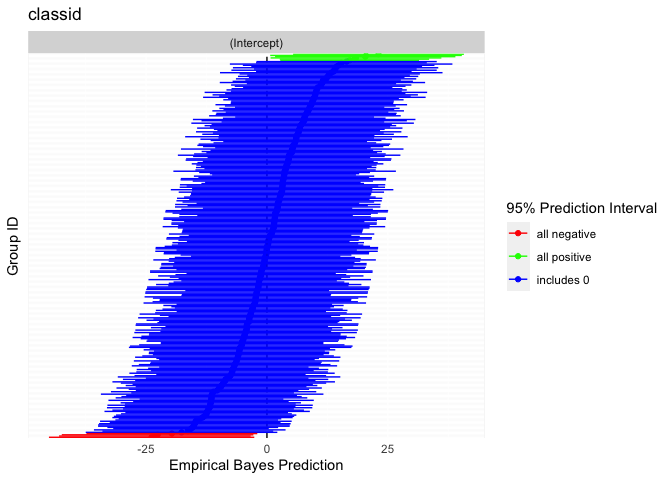
Rich visualizations of associations can be had along with caterpillar plots, which graph the 95% prediction intervals for the random effects.

# visualize between-group association
betweenPlot(x = "mathkind", y = "mathgain", grouping = "classid", dataset = instruction, xlab = "Kindergarten Math Score", ylab = "Gain in Math Score")

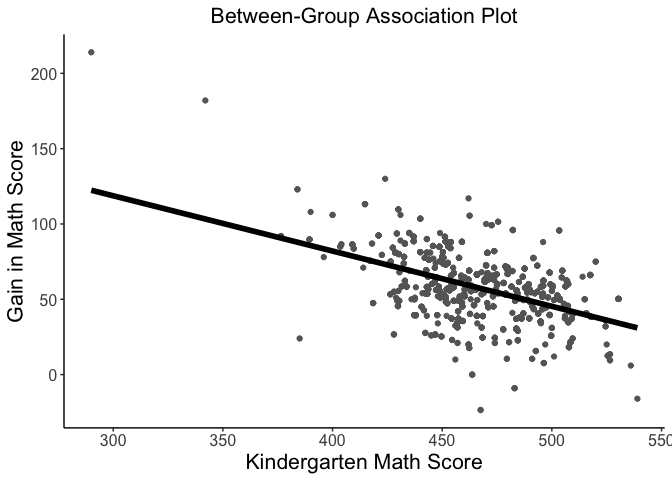
# visualze within-group association
withinPlot(x = "mathkind", y = "mathgain", grouping = "classid", dataset = instruction)

# caterpillar plot
caterpillarPlot(fit2, grouping = "classid")
#> [1] "classid"