Multivariate Difference Between Two Groups.
multid
multid provides tools for regularized measurement of multivariate differences between two groups (e.g., sex differences). Regularization via logistic regression variants enables inclusion of large number of correlated variables in the multivariate set while providing k-fold cross-validation and regularization to avoid overfitting (D_regularized -function).
See fully reproducible exemplary vignette on multivariate sex differences in personality with regularized regression, or the examples presented below.
Predictive approach as implemented with regularized methods also allows for examination of group-membership probabilities and their distributions across individuals. In the context of statistical predictions of sex, these distributions are an updated variant to gender-typicality distributions used in gender diagnosticity methodology (Lippa & Connelly, 1990).
Studies in which these methods have been used:
multid also includes a function for testing several hypotheses that are typically compressed to correlation between predictor (x) and an algebraic difference score (y1-y2) by deconstructing this difference score correlation. Deconstructing difference score correlations can be applied with structural path models (ddsc_sem) and multi-level models (ddsc_ml).
In addition, multid includes various helper functions:
Calculation of variance partition coefficient (i.e., intraclass correlation, ICC) with vpc_at -function at different levels of lower-level predictors in two-level model including random slope fitted with lmer (Goldstein et al., 2002)
Calculation of coefficient of variance variation and standardized variance heterogeneity, either with manual input of estimates (cvv_manual) or directly from data (cvv) (Ruscio & Roche, 2012)
Calculation of reliability of difference score variable that is a difference between two mean values (e.g., difference between men and women across countries) by using ICC2 reliability estimates (Bliese, 2000) as inputs in the equation for difference score reliability (Johns, 1981). Can be calculated from long format data file or from lmer-fitted two-level model with reliability_dms -function
Computing quantile correlation coefficient(s) with qcc - function defined as the geometric mean of two quantile regression slopes — that of X on Y and that of Y on X (Choi & Shin, 2022)
Installation
You can install the released version of multid from CRAN with:
install.packages("multid")
You can install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("vjilmari/multid")
Examples
Single sample with two groups
This example shows how to measure standardized multivariate (both Sepal and Petal dimensions, four variables in total) distance between setosa and versicolor Species in iris dataset.
library(multid)
set.seed(91237)
D.iris<-
D_regularized(
data = iris[iris$Species == "setosa" | iris$Species == "versicolor", ],
mv.vars = c(
"Sepal.Length", "Sepal.Width",
"Petal.Length", "Petal.Width"
),
group.var = "Species",
group.values = c("setosa", "versicolor")
)
round(D.iris$D,2)
#> n.setosa n.versicolor m.setosa m.versicolor sd.setosa sd.versicolor
#> [1,] 50 50 8.35 -9.38 1.39 2.25
#> pooled.sd diff D
#> [1,] 1.87 17.73 9.49
# Use different partitions of data for regularization and estimation
D.iris_out<-
D_regularized(
data = iris[iris$Species == "setosa" |
iris$Species == "versicolor", ],
mv.vars = c(
"Sepal.Length", "Sepal.Width",
"Petal.Length", "Petal.Width"
),
group.var = "Species",
group.values = c("setosa", "versicolor"),
size = 35,
out = TRUE,
pred.prob = TRUE,
prob.cutoffs = seq(0,1,0.25)
)
# print group differences (D)
round(D.iris_out$D,2)
#> n.setosa n.versicolor m.setosa m.versicolor sd.setosa sd.versicolor
#> [1,] 15 15 7.61 -8.97 1.79 2.35
#> pooled.sd diff D
#> [1,] 2.09 16.59 7.93
# print table of predicted probabilities
D.iris_out$P.table
#>
#> [0,0.25) [0.25,0.5) [0.5,0.75) [0.75,1]
#> setosa 0 0 0 1
#> versicolor 1 0 0 0
Multiple samples with two groups in each
This example first generates artificial multi-group data which are then used as separate data folds in the regularization procedure following separate predictions made for each fold.
# generate data for 10 groups
set.seed(34246)
n1 <- 100
n2 <- 10
d <-
data.frame(
sex = sample(c("male", "female"), n1 * n2, replace = TRUE),
fold = sample(x = LETTERS[1:n2], size = n1 * n2, replace = TRUE),
x1 = rnorm(n1 * n2),
x2 = rnorm(n1 * n2),
x3 = rnorm(n1 * n2)
)
#'
# Fit and predict with same data
round(D_regularized(
data = d,
mv.vars = c("x1", "x2", "x3"),
group.var = "sex",
group.values = c("female", "male"),
fold.var = "fold",
fold = TRUE,
rename.output = TRUE
)$D,2)
#> n.female n.male m.female m.male sd.female sd.male pooled.sd diff D
#> A 53 48 0.01 -0.02 0.07 0.06 0.07 0.04 0.53
#> B 56 53 0.00 -0.02 0.07 0.06 0.07 0.02 0.27
#> C 39 56 -0.02 -0.01 0.08 0.06 0.07 -0.01 -0.18
#> D 53 58 0.00 -0.01 0.06 0.06 0.06 0.01 0.17
#> E 44 52 0.00 0.01 0.06 0.07 0.06 -0.01 -0.14
#> F 60 31 -0.01 -0.01 0.06 0.06 0.06 -0.01 -0.10
#> G 56 51 -0.01 -0.03 0.06 0.05 0.06 0.01 0.20
#> H 47 51 0.00 -0.01 0.07 0.07 0.07 0.01 0.14
#> I 42 45 0.02 -0.01 0.07 0.07 0.07 0.03 0.48
#> J 48 57 0.00 -0.01 0.05 0.07 0.06 0.01 0.10
#> pooled.sd.female pooled.sd.male pooled.sd.total d.sd.total
#> A 0.07 0.06 0.07 0.56
#> B 0.07 0.06 0.07 0.26
#> C 0.07 0.06 0.07 -0.19
#> D 0.07 0.06 0.07 0.16
#> E 0.07 0.06 0.07 -0.14
#> F 0.07 0.06 0.07 -0.10
#> G 0.07 0.06 0.07 0.18
#> H 0.07 0.06 0.07 0.15
#> I 0.07 0.06 0.07 0.49
#> J 0.07 0.06 0.07 0.10
#'
# Different partitions for regularization and estimation for each data fold.
# Request probabilities of correct classification (pcc) and
# area under the receiver operating characteristics (auc) for the output.
round(D_regularized(
data = d,
mv.vars = c("x1", "x2", "x3"),
group.var = "sex",
group.values = c("female", "male"),
fold.var = "fold",
size = 17,
out = TRUE,
fold = TRUE,
rename.output = TRUE,
pcc = TRUE,
auc = TRUE
)$D,2)
#> n.female n.male m.female m.male sd.female sd.male pooled.sd diff D
#> A 36 31 0.00 -0.01 0.18 0.15 0.17 0.00 0.03
#> B 39 36 -0.04 -0.04 0.16 0.15 0.15 -0.01 -0.04
#> C 22 39 -0.07 0.01 0.17 0.13 0.15 -0.08 -0.56
#> D 36 41 0.01 0.01 0.14 0.17 0.15 0.00 -0.01
#> E 27 35 -0.07 0.00 0.13 0.11 0.12 -0.07 -0.60
#> F 43 14 -0.04 0.04 0.17 0.17 0.17 -0.08 -0.47
#> G 39 34 -0.03 -0.04 0.12 0.15 0.14 0.01 0.07
#> H 30 34 0.04 0.01 0.16 0.15 0.16 0.03 0.18
#> I 25 28 0.02 -0.03 0.14 0.14 0.14 0.05 0.35
#> J 31 40 0.00 0.00 0.15 0.15 0.15 0.00 0.02
#> pcc.female pcc.male pcc.total auc pooled.sd.female pooled.sd.male
#> A 0.56 0.39 0.48 0.49 0.15 0.15
#> B 0.36 0.61 0.48 0.50 0.15 0.15
#> C 0.32 0.46 0.41 0.34 0.15 0.15
#> D 0.53 0.49 0.51 0.49 0.15 0.15
#> E 0.37 0.49 0.44 0.37 0.15 0.15
#> F 0.44 0.36 0.42 0.39 0.15 0.15
#> G 0.38 0.59 0.48 0.53 0.15 0.15
#> H 0.73 0.47 0.59 0.57 0.15 0.15
#> I 0.48 0.64 0.57 0.60 0.15 0.15
#> J 0.55 0.45 0.49 0.52 0.15 0.15
#> pooled.sd.total d.sd.total
#> A 0.15 0.03
#> B 0.15 -0.04
#> C 0.15 -0.54
#> D 0.15 -0.01
#> E 0.15 -0.48
#> F 0.15 -0.54
#> G 0.15 0.06
#> H 0.15 0.19
#> I 0.15 0.32
#> J 0.15 0.02
Comparison of Mahalanobis’ D and Regularized D when Difference in Population Exists
This example compares a measure of standardized distance between group centroids (Mahalanobis’ D) and a regularized variant provided in the multid-package in small-sample scenario when the distance between group centroids in the population is D = 1.
set.seed(8327482)
# generate data from sixteen correlated (r = .20) variables each with d = .50 difference
#(equals to Mahalanobis' D = 1)
k=16
r=0.2
d=0.5
n=200
# population correlation matrix
cor_mat<-matrix(ncol=k,nrow=k,rep(r,k*k))
diag(cor_mat)<-1
# population difference vector
d_vector<-rep(d,k)
# population Mahalanobis' D is exactly 1
sqrt(t(d_vector) %*% solve(cor_mat) %*% d_vector)
#> [,1]
#> [1,] 1
# generate data
library(MASS)
male.dat<-
data.frame(sex="male",
mvrnorm(n = n/2,
mu = 0.5*d_vector,
Sigma = cor_mat,empirical = F))
female.dat<-
data.frame(sex="female",
mvrnorm(n = n/2,
mu = -0.5*d_vector,
Sigma = cor_mat,empirical = F))
dat<-rbind(male.dat,female.dat)
# sample Mahalanobis' D
# obtain mean differences
d_vector_sample<-rep(NA,k)
for (i in 1:k){
d_vector_sample[i]<-mean(male.dat[,i+1]-female.dat[,i+1])
}
# sample pooled covariance matrix (use mean, because equal sample sizes)
cov_mat_sample<-
(cov(male.dat[,2:17])+cov(female.dat[,2:17]))/2
# calculate sample Mahalanobis' D
sqrt(t(d_vector_sample) %*% solve(cov_mat_sample) %*% d_vector_sample)
#> [,1]
#> [1,] 1.265318
# calculate elastic net D
D.ela<-
D_regularized(data=dat,
mv.vars=paste0("X",1:k),
group.var = "sex",
group.values = c("male","female"))
round(D.ela$D,2)
#> n.male n.female m.male m.female sd.male sd.female pooled.sd diff D
#> [1,] 100 100 0.58 -0.58 0.89 0.99 0.94 1.16 1.23
# use separate data for regularization and estimation
D.ela_out<-D_regularized(data=dat,
mv.vars=paste0("X",1:k),
group.var = "sex",
group.values = c("male","female"),
out=T,size = 50,pcc = T, auc=T,pred.prob = T)
round(D.ela_out$D,2)
#> n.male n.female m.male m.female sd.male sd.female pooled.sd diff D
#> [1,] 50 50 0.63 -0.34 1.14 1.01 1.08 0.97 0.9
#> pcc.male pcc.female pcc.total auc
#> [1,] 0.66 0.58 0.62 0.73
# Table of predicted probabilites
D.ela_out$P.table
#>
#> [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8) [0.8,1]
#> female 0.14 0.28 0.32 0.22 0.04
#> male 0.00 0.22 0.16 0.38 0.24
Comparison of Mahalanobis’ D and Regularized D when Sex Difference in Population Does Not Exist
This example compares a measure of standardized distance between group centroids (Mahalanobis’ D) and a regularized variant provided in the multid-package in small-sample scenario when the group centroids in the population is are at the same location, D = 0. In this sample, Mahalanobis’ D is measured at D = 0.5, elastic net D with same data used for regularization and estimation at D = 0.35, whereas elastic net D with independent estimation data shows D = 0.
set.seed(8327482)
# generate data from sixteen correlated (r = .20) variables each with d = .00 difference
# (equals to Mahalanobis' D = 0)
k=16
r=0.2
d=0.0
n=200
# population correlation matrix
cor_mat<-matrix(ncol=k,nrow=k,rep(r,k*k))
diag(cor_mat)<-1
# population difference vector
d_vector<-rep(d,k)
# population Mahalanobis' D is exactly 1
sqrt(t(d_vector) %*% solve(cor_mat) %*% d_vector)
#> [,1]
#> [1,] 0
# generate data
male.dat<-
data.frame(sex="male",
mvrnorm(n = n/2,
mu = 0.5*d_vector,
Sigma = cor_mat,empirical = F))
female.dat<-
data.frame(sex="female",
mvrnorm(n = n/2,
mu = -0.5*d_vector,
Sigma = cor_mat,empirical = F))
dat<-rbind(male.dat,female.dat)
# sample Mahalanobis' D
# obtain mean differences
d_vector_sample<-rep(NA,k)
for (i in 1:k){
d_vector_sample[i]<-mean(male.dat[,i+1]-female.dat[,i+1])
}
# sample pooled covariance matrix (use mean, because equal sample sizes)
cov_mat_sample<-
(cov(male.dat[,2:17])+cov(female.dat[,2:17]))/2
# calculate sample Mahalanobis' D
sqrt(t(d_vector_sample) %*% solve(cov_mat_sample) %*% d_vector_sample)
#> [,1]
#> [1,] 0.5316555
# calculate elastic net D
D.ela.zero<-
D_regularized(data=dat,
mv.vars=paste0("X",1:k),
group.var = "sex",
group.values = c("male","female"))
round(D.ela.zero$D,2)
#> n.male n.female m.male m.female sd.male sd.female pooled.sd diff D
#> [1,] 100 100 0 0 0 0 0 0 NaN
# use separate data for regularization and estimation
D.ela.zero_out<-
D_regularized(data=dat,
mv.vars=paste0("X",1:k),
group.var = "sex",
group.values = c("male","female"),
out=T,size = 50,pcc = T, auc=T,pred.prob = T)
round(D.ela.zero_out$D,2)
#> n.male n.female m.male m.female sd.male sd.female pooled.sd diff D
#> [1,] 50 50 0.04 0.03 0.25 0.24 0.24 0.01 0.04
#> pcc.male pcc.female pcc.total auc
#> [1,] 0.58 0.46 0.52 0.51
# Table of predicted probabilites
D.ela.zero_out$P.table
#>
#> [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8) [0.8,1]
#> female 0.00 0.04 0.94 0.02 0.00
#> male 0.00 0.02 0.92 0.06 0.00
Distribution overlap
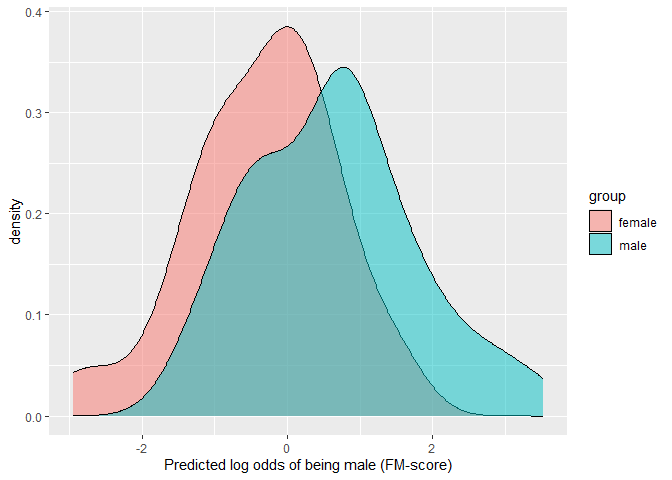
This example shows how the degree of overlap between the predicted values across the two groups can be visualized and estimated.
For parametric variants, see Del Giudice (2022).
For non-parametric variants, see Pastore (2018) and Pastore & Calcagnì (2019).
# Use predicted values from elastic net D (out) when difference in population exists-
library(ggplot2)
ggplot(D.ela_out$pred.dat,
aes(x=pred,fill=group))+
geom_density(alpha=0.5)+
xlab("Predicted log odds of being male (FM-score)")
# parametric overlap
## Proportion of overlap relative to a single distribution (OVL)
## obtain D first
(D<-unname(D.ela_out$D[,"D"]))
#> [1] 0.9004981
(OVL<-2*pnorm((-D/2)))
#> [1] 0.6525309
## Proportion of overlap relative to the joint distribution
(OVL2<-OVL/(2-OVL))
#> [1] 0.484264
# non-parametric overlap
library(overlapping)
np.overlap<-
overlap(x = list(D.ela_out$pred.dat[
D.ela_out$pred.dat$group=="male","pred"],
D.ela_out$pred.dat[
D.ela_out$pred.dat$group=="female","pred"]),
plot=T)
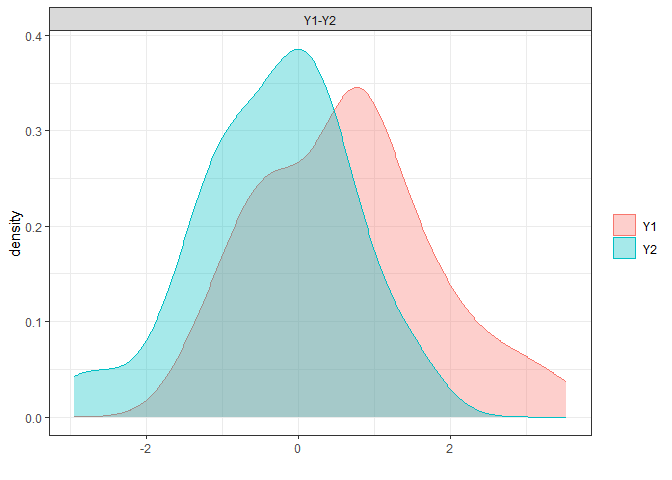
# this corresponds to Proportion of overlap relative to the joint distribution (OVL2)
(np.OVL2<-unname(np.overlap$OV))
#> [1] 0.6980442
# from which Proportion of overlap relative to a single distribution (OVL) is approximated at
(np.OVL<-(2*np.OVL2)/(1+np.OVL2))
#> [1] 0.8221744
# compare overlaps
round(cbind(OVL,np.OVL,OVL2,np.OVL2),2)
#> OVL np.OVL OVL2 np.OVL2
#> [1,] 0.65 0.82 0.48 0.7
Predicting Difference Scores
# sem example
set.seed(342356)
d <- data.frame(
var1 = rnorm(50),
var2 = rnorm(50),
x = rnorm(50)
)
round(ddsc_sem(
data = d, y1 = "var1", y2 = "var2",
x = "x",
)$results,3)
#> est se z pvalue ci.lower ci.upper
#> r_xy1_y2 0.121 0.140 0.865 0.387 -0.154 0.397
#> r_xy1 0.099 0.141 0.703 0.482 -0.177 0.375
#> r_xy2 -0.086 0.141 -0.610 0.542 -0.362 0.190
#> b_11 0.107 0.152 0.703 0.482 -0.192 0.406
#> b_21 -0.078 0.128 -0.610 0.542 -0.329 0.173
#> b_10 -0.076 0.151 -0.507 0.612 -0.372 0.219
#> b_20 -0.015 0.127 -0.115 0.909 -0.263 0.234
#> res_cov_y1_y2 -0.153 0.137 -1.120 0.263 -0.422 0.115
#> diff_b10_b20 -0.062 0.212 -0.292 0.770 -0.478 0.354
#> diff_b11_b21 0.185 0.214 0.865 0.387 -0.235 0.605
#> diff_rxy1_rxy2 0.185 0.215 0.862 0.389 -0.236 0.605
#> q_b11_b21 0.186 0.216 0.860 0.390 -0.238 0.610
#> q_rxy1_rxy2 0.185 0.216 0.857 0.391 -0.239 0.610
#> cross_over_point 0.334 1.208 0.276 0.782 -2.034 2.702
#> sum_b11_b21 0.029 0.183 0.158 0.875 -0.329 0.387
#> main_effect 0.014 0.091 0.158 0.875 -0.165 0.193
#> interaction_vs_main_effect 0.171 0.218 0.784 0.433 -0.256 0.598
#> diff_abs_b11_abs_b21 0.029 0.183 0.158 0.875 -0.329 0.387
#> abs_diff_b11_b21 0.185 0.214 0.865 0.194 -0.235 0.605
#> abs_sum_b11_b21 0.029 0.183 0.158 0.437 -0.329 0.387
#> dadas 0.157 0.256 0.610 0.271 -0.346 0.659
#> q_r_equivalence 0.185 0.216 0.857 0.804 NA NA
#> q_b_equivalence 0.186 0.216 0.860 0.805 NA NA
#> cross_over_point_equivalence 0.334 1.208 0.276 0.609 NA NA
#> cross_over_point_minimal_effect 0.334 1.208 0.276 0.391 NA NA
# multilevel example
set.seed(95332)
n1 <- 10 # groups
n2 <- 10 # observations per group
dat <- data.frame(
group = rep(c(LETTERS[1:n1]), each = n2),
w = sample(c(-0.5, 0.5), n1 * n2, replace = TRUE),
x = rep(sample(1:5, n1, replace = TRUE), each = n2),
y = sample(1:5, n1 * n2, replace = TRUE)
)
library(lmerTest)
fit <- lmerTest::lmer(y ~ x * w + (w | group),
data = dat
)
round(ddsc_ml(fit,
predictor = "x",
moderator = "w",
moderator_values = c(0.5, -0.5))$results, 3)
#> estimate SE df t.ratio p.value ci.lower
#> r_xy1y2 -0.229 0.258 7.071 -0.886 0.405 -0.838
#> w_11 -0.279 0.136 9.326 -2.048 0.070 -0.586
#> w_21 -0.077 0.177 8.053 -0.435 0.675 -0.485
#> r_xy1 -0.453 0.221 9.326 -2.048 0.070 -0.952
#> r_xy2 -0.113 0.260 8.053 -0.435 0.675 -0.713
#> b_11 -0.431 0.211 9.326 -2.048 0.070 -0.905
#> b_21 -0.119 0.273 8.053 -0.435 0.675 -0.748
#> main_effect -0.178 0.109 6.952 -1.630 0.147 -0.437
#> moderator_effect 1.039 0.733 7.204 1.417 0.198 -0.685
#> interaction -0.202 0.228 7.071 -0.886 0.405 -0.741
#> q_b11_b21 -0.342 NA NA NA NA NA
#> q_rxy1_rxy2 -0.375 NA NA NA NA NA
#> cross_over_point 5.134 NA NA NA NA NA
#> interaction_vs_main 0.024 0.277 8.196 0.087 0.933 -0.613
#> interaction_vs_main_bscale 0.037 0.428 8.196 0.087 0.933 -0.945
#> interaction_vs_main_rscale 0.057 0.411 8.157 0.138 0.893 -0.888
#> dadas -0.154 0.354 8.053 -0.435 0.662 -0.970
#> dadas_bscale -0.238 0.547 8.053 -0.435 0.662 -1.497
#> dadas_rscale -0.227 0.521 8.053 -0.435 0.662 -1.426
#> abs_diff 0.202 0.228 7.071 0.886 0.202 -0.337
#> abs_sum 0.356 0.219 6.952 1.630 0.074 -0.161
#> abs_diff_bscale 0.312 0.352 7.071 0.886 0.202 -0.519
#> abs_sum_bscale 0.550 0.337 6.952 1.630 0.074 -0.249
#> abs_diff_rscale 0.340 0.349 6.956 0.973 0.181 -0.487
#> abs_sum_rscale 0.567 0.334 7.065 1.696 0.067 -0.222
#> ci.upper
#> r_xy1y2 0.381
#> w_11 0.028
#> w_21 0.331
#> r_xy1 0.045
#> r_xy2 0.487
#> b_11 0.043
#> b_21 0.511
#> main_effect 0.081
#> moderator_effect 2.763
#> interaction 0.337
#> q_b11_b21 NA
#> q_rxy1_rxy2 NA
#> cross_over_point NA
#> interaction_vs_main 0.661
#> interaction_vs_main_bscale 1.020
#> interaction_vs_main_rscale 1.001
#> dadas 0.662
#> dadas_bscale 1.021
#> dadas_rscale 0.973
#> abs_diff 0.741
#> abs_sum 0.874
#> abs_diff_bscale 1.144
#> abs_sum_bscale 1.349
#> abs_diff_rscale 1.167
#> abs_sum_rscale 1.355