Sensitivity Analysis of Omitted Variable Bias.

ovbsa

The goal of ovbsa (omitted variable bias sensitivity analysis) is to conduct sensitivity analysis of omitted variable bias in linear econometrics models. For details see Basu (2025).

Installation

You can install the package ovbsa from CRAN with:

# uncomment this line
# install.packages("ovbsa")

You can install the development version of ovbsa from GitHub with:

# uncomment these lines
# install.packages("pak")
# pak::pak("dbasu-umass/ovbsa")

Main functions

The main functions in this package are:

• bsal: this function conducts basic sensitivity analysis (bsal) and reports the bias-adjusted estimate, the bias-adjusted standard error and the bias-adjusted confidence interval in a linear regression model;

• saltr2: this function computes the probability of the conclusion of the study being overturned using the total R-squared-based analysis;

• salpr2ncd: this function computes the probability of the conclusion of the study being overturned using the partial R-squared-based analysis without conditioning on the treatment variable;

Let us first load the relevant libraries and then work through two examples.

library(ovbsa)
library(sensemakr)
#> See details in:
#> Carlos Cinelli and Chad Hazlett (2020). Making Sense of Sensitivity: Extending Omitted Variable Bias. Journal of the Royal Statistical Society, Series B (Statistical Methodology).

library(ggplot2)

In the examples we will use use the data set darfur from the package sensemakr, which studies the effect of exposure to violence on attitudes towards peace.

Example 1: Bias-adjusted confidence interval

This is a basic example which shows you how to find the bias-adjusted estimate, the bias-adjusted standard error and the bias-adjusted confidence interval in a linear regression model. To use this function the user needs to choose a benchmark covariate, values of the sensitivity parameters kD and kY and the significance level alpha for testing the null hypothesis that the treatment effect is zero.

Here we choose the benchmark covariate as female, kD=3, kY=3 and alpha=0.05

## basic example code
analysis1 <- ovbsa::bsal(
  kd=3,ky=3,alpha=0.05,data=darfur,
  outcome = "peacefactor",
  treatment = "directlyharmed",
  bnch_reg = "female",
  other_reg = c("village","age","farmer_dar","herder_dar",
                "pastvoted","hhsize_darfur")
)

Now, let us see the results.

(analysis1)
#>                        Case 1       Case 2
#> r2yd.x            0.021873093  0.021873093
#> r2dz.x            0.008040002  0.027492860
#> r2yz.dx           0.781414454  0.380969988
#> estimate          0.097315819  0.097315819
#> adjusted_estimate 0.045525612  0.029779889
#> adjusted_se       0.010924114  0.018566585
#> adjusted_lower_CI 0.024081595 -0.006666285
#> adjusted_upper_CI 0.066969628  0.066226063

Here Case 1 refers to the total R-squared-based approach; Case 2 refers to the partial R-squared-based approach without conditioning on the treatment variable.

Example 2: Probability of study’s conclusion being overturned

Continuing with the previous example, we will now compute the probability that taking account of omitted variable bias will overturn the conclusion of the study. We will need to choose the significance level alpha for testing the null hypothesis that the treatment effect is zero, the mode (and median) k_kd of the parameter kD, and the mode (and median) k_ky of the parameter kY.

Here we choose alpha=0.05, k_kd=1, k_ky=1.

First, we will look at total R-squared based analysis:

# total r2-based analysis
res1 <- ovbsa::saltr2(
  alpha=0.05,data = darfur, outcome = "peacefactor",
  treatment = "directlyharmed", bnch_reg = "female",
  other_reg = c("village","age","farmer_dar","herder_dar",
                "pastvoted","hhsize_darfur"),
  N = 500, k_kd=1, k_ky=1
)
# probability
(res1$frac_prob_wt)
#> [1] 0.2582741

Second: we will see the partial R-squared based analysis without conditioning on the treatment variable:

res2 <- ovbsa::salpr2ncd(
  alpha=0.05,data = darfur, outcome = "peacefactor",
  treatment = "directlyharmed", bnch_reg = "female",
  other_reg = c("village","age","farmer_dar","herder_dar",
                "pastvoted","hhsize_darfur"),
  N = 500, k_kd=1, k_ky=1
)
# probability
(res2$frac_prob_wt)
#> [1] 0.3118923

Example 3: Contour plot of boundary of bias-adjusted confidence interval

The above functions used to compute the probability of a study’s conclusion being overturned implicitly used a contour plot of the boundary of the bias-adjusted confidence interval. The data is available as an output to be used by researchers to create that plot, if needed.

I will use the output of the total R-squared-based analysis to create the contour plot. The data frame to construct the contour plot is available as a data frame in res1$dataplot. For the contour plot, we will need three variables from this data frame: X1 as the x-axis, X2 as the y-axis and Z3 as the z-axis (value of the lower boundary of the bias-adjusted confidence interval).

# the contour plot  
ggplot(data = res1$dataplot, aes(X1, X2, z = Z3)) +
      geom_contour() +
      geom_contour_filled() +
      labs(
        title = "Contour plot of lower boundary of bias-adj CI",
        subtitle = "Total R2-based covariate benchmarking"
      ) +
      xlab(expression(k[D])) +
      ylab(expression(k[Y])) +
      theme_minimal()
#> Warning: Removed 96443 rows containing non-finite outside the scale range
#> (`stat_contour()`).
#> Warning: Removed 96443 rows containing non-finite outside the scale range
#> (`stat_contour_filled()`).

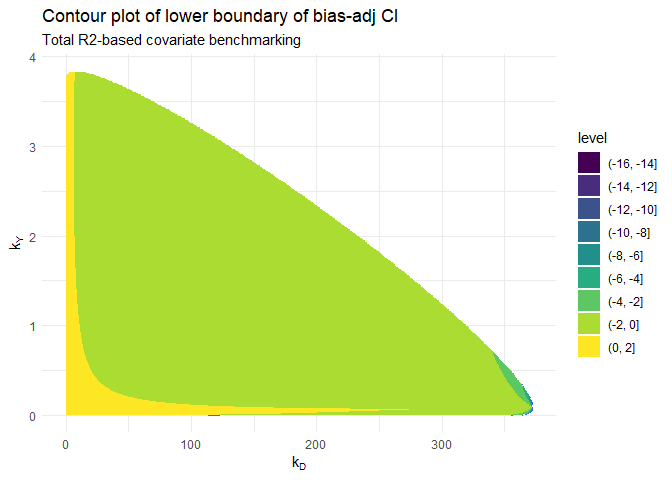
For easy reference, the following information about the relevant variables in the data frame should be noted while constructing contour plots like the one above:

• when the unadjusted estimate is positive, use X1 as the x-axis, X2 as the y-axis and Z3 as the z-axis (value of the lower boundary of the bias-adjusted confidence interval);

• when the unadjusted estimate is negative, use X1 as the x-axis, X2 as the y-axis and Z4 as the z-axis (value of the lower boundary of the bias-adjusted confidence interval).

References

• Basu, D. (2025). How likely is it that omitted variable bias will overturn your results? SSRN Working Paper. Available here: doi:10.2139/ssrn.4704246