Average Bioequivalence with Expanding Limits (ABEL).

replicateBE

• Introduction
  • Methods
    • Estimation of CV_wR (and CV_wT in full replicate designs)
    • Method A
    • Method /a
    • Average Bioequivalence
  • Tested designs
    • Four period (full) replicates
    • Three period (full) replicates
    • Two period (full) replicate
    • Three period (partial) replicates
  • Cross-validation
• Examples
• Installation
• Session Information
• Contributors
• Disclaimer

Version 1.1.3 built 2022-05-02 with R 4.2.0 (development version not on CRAN).

Comparative BA-calculation for the EMA’s Average Bioequivalence with Expanding Limits (ABEL)

Introduction

The package provides data sets (internal .rda and in -format in /extdata/) supporting users in a black-box performance qualification (PQ) of their software installations. Users can analyze own data imported from - and Excel-files (in xlsx or the legacy xls format). The methods given by the for reference-scaling of , i.e., Average Bioequivalence with Expanding Limits (ABEL)^1,2 are implemented.
Potential influence of outliers on the variability of the reference can be assessed by box plots of studentized and standardized residuals as suggested at a joint / workshop.³
Health Canada’s approach⁴ requiring a mixed-effects model is approximated by intra-subject contrasts.
Direct widening of the acceptance range as recommended by the Gulf Cooperation Council⁵ (Bahrain, Kuwait, Oman, Qatar, Saudi Arabia, United Arab Emirates) is provided as well.
In full replicate designs the variability of test and reference treatments can be assessed by s_wT/s_wR and the upper confidence limit of σ_wT/σ_wR. This was required in a pilot phase by the but lifted in 2021; reference-scaling of AUC is acceptable if the protocol is submitted to the .⁶

TOC ↩

Methods

Estimation of CV_wR (and CV_wT in full replicate designs)

Called internally by functions method.A() and method.B(). A linear model of log-transformed pharmacokinetic (PK) responses and effects
sequence, subject(sequence), period
where all effects are fixed (i.e., by an ). Estimated by the function lm() of package stats.

modCVwR <- lm(log(PK) ~ sequence + subject%in%sequence + period,
                        data = data[data$treatment == "R", ])
modCVwT <- lm(log(PK) ~ sequence + subject%in%sequence + period,
                        data = data[data$treatment == "T", ])

TOC ↩

Method A

Called by function method.A(). A linear model of log-transformed responses and effects
sequence, subject(sequence), period, treatment
where all effects are fixed (e.g., by an ). Estimated by the function lm() of package stats.

modA <- lm(log(PK) ~ sequence + subject%in%sequence + period + treatment,
                     data = data)

TOC ↩

Method B

Called by function method.B(). A linear model of log-transformed responses and effects
sequence, subject(sequence), period, treatment
where subject(sequence) is a random effect and all others are fixed.
Three options are provided:

• Estimation by the function lmer() of package lmerTest. method.B(..., option = 1) employs Satterthwaite’s approximation of the degrees of freedom equivalent to SAS’ DDFM=SATTERTHWAITE, Phoenix WinNonlin’s Degrees of Freedom Satterthwaite, and Stata’s dfm=Satterthwaite. Note that this is the only available approximation in SPSS.

modB <- lmer(log(PK) ~ sequence + period + treatment + (1|subject),
                       data = data)

• Estimation by the function lme() of package nlme. method.B(..., option = 2) employs degrees of freedom equivalent to SAS’ DDFM=CONTAIN, Phoenix WinNonlin’s Degrees of Freedom Residual, STATISTICA’s GLM containment, and Stata’s dfm=anova. Implicitly preferred according to the ’s document and hence, the default of the function.

modB <- lme(log(PK) ~ sequence +  period + treatment, random = ~1|subject,
                      data = data)

• Estimation by the function lmer() of package lmerTest. method.B(..., option = 3) employs the Kenward-Roger approximation equivalent to Stata’s dfm=Kenward Roger (EIM) and SAS’ DDFM=KENWARDROGER(FIRSTORDER)i.e., based on the expected information matrix. Note that SAS with DDFM=KENWARDROGER and JMP calculate Satterthwaite’s [sic] degrees of freedom and apply the Kackar-Harville correction, i.e., based on the observed information matrix.

modB <- lmer(log(PK) ~ sequence + period + treatment + (1|subject),
                       data = data)

TOC ↩

Average Bioequivalence

Called by function ABE(). The model is identical to Method A. Conventional BE limits (80.00 – 125.00%) are employed by default. Tighter limits (90.00 – 111.11%) for narrow therapeutic index drugs ( and others) or wider limits (75.00 – 133.33%) for C_max according to the guideline of South Africa⁷ can be specified.

TOC ↩

Tested designs

Four period (full) replicates

TRTR | RTRT
TRRT | RTTR
TTRR | RRTT
TRTR | RTRT | TRRT | RTTR
TRRT | RTTR | TTRR | RRTT

Three period (full) replicates

TRT | RTR
TRR | RTT

Two period (full) replicate

TR | RT | TT | RR(Balaam’s design; not recommended due to poor power characteristics)

Three period (partial) replicates

TRR | RTR | RRT
TRR | RTR(Extra-reference design; biased in the presence of period effects, not recommended)

TOC ↩

Cross-validation

Details about the reference datasets:

help("data", package = "replicateBE")
?replicateBE::data

Results of the 30 reference datasets agree with ones obtained in SAS (v9.4), Phoenix WinNonlin (v6.4 – v8.3.4.295), STATISTICA (v13), SPSS (v22.0), Stata (v15.0), and JMP (v10.0.2).⁸

TOC ↩

Examples

• Evaluation of the internal reference dataset 01⁹ by Method A.

library(replicateBE) # attach the package
res <- method.A(verbose = TRUE, details = TRUE,
                print = FALSE, data = rds01)
# 
# Data set DS01: Method A by lm() 
# ─────────────────────────────────── 
# Type III Analysis of Variance Table
# 
# Response: log(PK)
#                   Df   Sum Sq  Mean Sq  F value     Pr(>F)
# sequence           1   0.0077 0.007652  0.00268  0.9588496
# period             3   0.6984 0.232784  1.45494  0.2278285
# treatment          1   1.7681 1.768098 11.05095  0.0010405
# sequence:subject  75 214.1296 2.855061 17.84467 < 2.22e-16
# Residuals        217  34.7190 0.159995                    
# 
# treatment T – R:
#   Estimate Std. Error    t value   Pr(>|t|) 
# 0.14547400 0.04650870 3.12788000 0.00200215 
# 217 Degrees of Freedom
cols <- c(12, 17:21)           # extract relevant columns
# cosmetics: 2 decimal places acc. to the GL
tmp  <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp  <- cbind(tmp, res[22:24]) # pass|fail
print(tmp, row.names = FALSE)
#  CVwR(%)  L(%)   U(%) CL.lo(%) CL.hi(%)  PE(%)   CI  GMR   BE
#    46.96 71.23 140.40   107.11   124.89 115.66 pass pass pass

TOC ↩

• The same dataset evaluated by Method B, Satterthwaite approximation of degrees of freedom.

res  <- method.B(option = 1, verbose = TRUE, details = TRUE,
                 print = FALSE, data = rds01)
# 
# Data set DS01: Method B (option = 1) by lmer() 
# ────────────────────────────────────────────── 
# Response: log(PK)
# Type III Analysis of Variance Table with Satterthwaite's method
#             Sum Sq  Mean Sq NumDF    DenDF F value    Pr(>F)
# sequence  0.001917 0.001917     1  74.7208 0.01198 0.9131536
# period    0.398078 0.132693     3 217.1188 0.82881 0.4792840
# treatment 1.579332 1.579332     1 216.9386 9.86464 0.0019197
# 
# treatment T – R:
#   Estimate Std. Error    t value   Pr(>|t|) 
#  0.1460900  0.0465130  3.1408000  0.0019197 
# 216.939 Degrees of Freedom (equivalent to SAS’ DDFM=SATTERTHWAITE)
cols <- c(12, 17:21)
tmp  <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp  <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
#  CVwR(%)  L(%)   U(%) CL.lo(%) CL.hi(%)  PE(%)   CI  GMR   BE
#    46.96 71.23 140.40   107.17   124.97 115.73 pass pass pass

TOC ↩

• The same dataset evaluated by Method B, Kenward-Roger approximation of degrees of freedom. Outlier assessment, recalculation of CV_wR after exclusion of outliers, new expanded limits.

res  <- method.B(option = 3, ola = TRUE, verbose = TRUE,
                 details = TRUE, print = FALSE, data = rds01)

# 
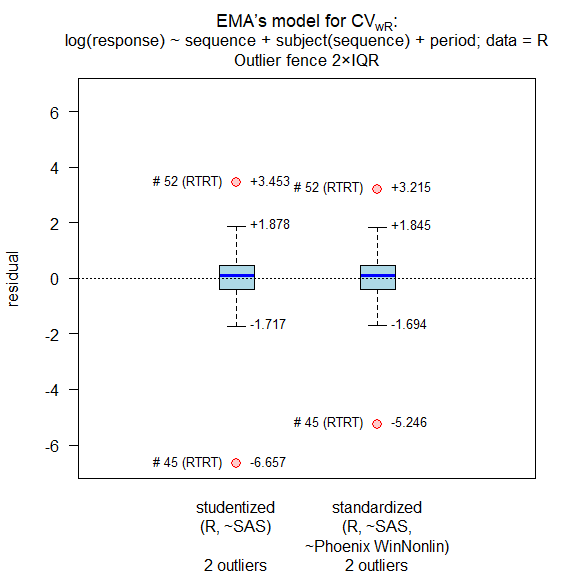
# Outlier analysis
#  (externally) studentized residuals
#  Limits (2×IQR whiskers): -1.717435, 1.877877
#  Outliers:
#  subject sequence  stud.res
#       45     RTRT -6.656940
#       52     RTRT  3.453122
# 
#  standarized (internally studentized) residuals
#  Limits (2×IQR whiskers): -1.69433, 1.845333
#  Outliers:
#  subject sequence stand.res
#       45     RTRT -5.246293
#       52     RTRT  3.214663
# 
# Data set DS01: Method B (option = 3) by lmer() 
# ────────────────────────────────────────────── 
# Response: log(PK)
# Type III Analysis of Variance Table with Kenward-Roger's method
#             Sum Sq  Mean Sq NumDF    DenDF F value    Pr(>F)
# sequence  0.001917 0.001917     1  74.9899 0.01198 0.9131528
# period    0.398065 0.132688     3 217.3875 0.82878 0.4792976
# treatment 1.579280 1.579280     1 217.2079 9.86432 0.0019197
# 
# treatment T – R:
#   Estimate Std. Error    t value   Pr(>|t|) 
#  0.1460900  0.0465140  3.1408000  0.0019197 
# 217.208 Degrees of Freedom (equivalent to Stata’s dfm=Kenward Roger EIM)
cols <- c(27, 31:32, 19:21)
tmp  <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp  <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
#  CVwR.rec(%) L.rec(%) U.rec(%) CL.lo(%) CL.hi(%)  PE(%)   CI  GMR   BE
#        32.16    78.79   126.93   107.17   124.97 115.73 pass pass pass

TOC ↩

• The same dataset evaluated according to the conditions of the

res <- method.A(regulator = "GCC", details = TRUE,
                print = FALSE, data = rds01)
cols <- c(12, 17:21)
tmp  <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp  <- cbind(tmp, res[22:24])
print(tmp, row.names = FALSE)
#  CVwR(%)  L(%)   U(%) CL.lo(%) CL.hi(%)  PE(%)   CI  GMR   BE
#    46.96 75.00 133.33   107.11   124.89 115.66 pass pass pass

TOC ↩

• The same dataset evaluated according to the conditions of South Africa (if CV_wR > 30% fixed limits 75.00 – 133.33%).

res <- ABE(theta1 = 0.75, details = TRUE,
           print = FALSE, data = rds01)
tmp <- data.frame(as.list(sprintf("%.2f", res[12:17])))
names(tmp) <- names(res)[12:17]
tmp <- cbind(tmp, res[18])
print(tmp, row.names = FALSE)
#  CVwR(%) BE.lo(%) BE.hi(%) CL.lo(%) CL.hi(%)  PE(%)   BE
#    46.96    75.00   133.33   107.11   124.89 115.66 pass

TOC ↩

• Evaluation of the internal reference dataset 05.¹⁰ Tighter limits for the phenytoin.

res <- ABE(theta1 = 0.90, details = TRUE,
           print = FALSE, data = rds05)
cols <- c(13:17)
tmp  <- data.frame(as.list(sprintf("%.2f", res[cols])))
names(tmp) <- names(res)[cols]
tmp  <- cbind(tmp, res[18])
print(tmp, row.names = FALSE)
#  BE.lo(%) BE.hi(%) CL.lo(%) CL.hi(%)  PE(%)   BE
#     90.00   111.11   103.82   112.04 107.85 fail

TOC ↩

Installation

The package requires R ≥3.5.0. However, for the Kenward-Roger approximation method.B(..., option = 3) R ≥3.6.0 is required.

• Install the released version from :

install.packages("replicateBE", repos = "https://cloud.r-project.org/")

• To use the development version, please install the released version from CRAN first to get its dependencies right (readxl ≥1.0.0, PowerTOST ≥1.5.3, lmerTest, nlme, pbkrtest).

  You need tools for building R packages from sources on your machine. For Windows users:

  • Download Rtools from and follow the suggestions of the installer.
  • Install devtools and build the development version by:

install.packages("devtools", repos = "https://cloud.r-project.org/")
devtools::install_github("Helmut01/replicateBE")

TOC ↩

Session Information

Inspect this information for reproducibility. Of particular importance are the versions of R and the packages used to create this workflow. It is considered good practice to record this information with every analysis.

options(width = 66)
print(sessionInfo(), locale = FALSE)
# R version 4.2.0 (2022-04-22 ucrt)
# Platform: x86_64-w64-mingw32/x64 (64-bit)
# Running under: Windows 10 x64 (build 22000)
# 
# Matrix products: default
# 
# attached base packages:
# [1] stats     graphics  grDevices utils     datasets  methods  
# [7] base     
# 
# other attached packages:
# [1] replicateBE_1.1.3
# 
# loaded via a namespace (and not attached):
#  [1] tidyselect_1.1.2    xfun_0.30           purrr_0.3.4        
#  [4] splines_4.2.0       lmerTest_3.1-3      lattice_0.20-45    
#  [7] colorspace_2.0-3    vctrs_0.4.1         generics_0.1.2     
# [10] htmltools_0.5.2     yaml_2.3.5          utf8_1.2.2         
# [13] rlang_1.0.2         pillar_1.7.0        nloptr_2.0.0       
# [16] glue_1.6.2          PowerTOST_1.5-4     readxl_1.4.0       
# [19] lifecycle_1.0.1     stringr_1.4.0       munsell_0.5.0      
# [22] gtable_0.3.0        cellranger_1.1.0    mvtnorm_1.1-3      
# [25] evaluate_0.15       knitr_1.39          fastmap_1.1.0      
# [28] parallel_4.2.0      pbkrtest_0.5.1      fansi_1.0.3        
# [31] highr_0.9           broom_0.8.0         Rcpp_1.0.8.3       
# [34] backports_1.4.1     scales_1.2.0        lme4_1.1-29        
# [37] TeachingDemos_2.12  ggplot2_3.3.5       digest_0.6.29      
# [40] stringi_1.7.6       dplyr_1.0.8         numDeriv_2016.8-1.1
# [43] grid_4.2.0          cli_3.3.0           tools_4.2.0        
# [46] magrittr_2.0.3      tibble_3.1.6        tidyr_1.2.0        
# [49] crayon_1.5.1        pkgconfig_2.0.3     MASS_7.3-57        
# [52] ellipsis_0.3.2      Matrix_1.4-1        minqa_1.2.4        
# [55] rmarkdown_2.14      rstudioapi_0.13     cubature_2.0.4.4   
# [58] R6_2.5.1            boot_1.3-28         nlme_3.1-157       
# [61] compiler_4.2.0

TOC ↩

Contributors

Helmut Schütz (author) ORCID iD
Michael Tomashevskiy (contributor)
Detlew Labes (contributor) <span style="font-size:smaller">ORCID iD

TOC ↩

Disclaimer

Package offered for Use without any Guarantees and Absolutely No Warranty. No Liability is accepted for any Loss and Risk to Public Health Resulting from Use of this R-Code.

TOC ↩

  1. . EMA/582648/2016. Annex I. London. 21 September 2016. Online↩
  2. , . CPMP/EWP/QWP/1401/98 Rev. 1/ Corr **. London. 20 January 2010. Online.↩
  3. . Revised EMA Bioequivalence Guideline. Questions & Answers. London. June 2010. Online↩
  4. Health Canada. Guidance Document. Conduct and Analysis of Comparative Bioavailability Studies. Ottawa. 2018/06/08. Online.↩
  5. Executive Board of the Health Ministers’ Council for ↩
  6. . Application of reference-scaled criteria for AUC in bioequivalence studies conducted for submission to . Geneva. 02 July 2021. Online.↩
  7. ↩
  8. Schütz H, Tomashevskiy M, Labes D, Shitova A, González-de la Parra M, Fuglsang A. Reference Datasets for Studies in a Replicate Design Intended for Average Bioequivalence with Expanding Limits. AAPS J. 2020; 22(2): Article 44. doi:10.1208/s12248-020-0427-6.↩
  9. . EMA/582648/2016. Annex II. London. 21  September 2016. Online.↩
10. Shumaker RC, Metzler CM. The Phenytoin Trial is a Case Study of ‘Individual’ Bioequivalence. Drug Inf J. 1998; 32(4): 1063–72. doi:10.1177/009286159803200426.↩