The Johnson Quantile-Parameterised Distribution.

The Johnson Quantile-Parameterised Distribution

The goal of rjqpd is to implement the Johnson Quantile-Parameterised distribution system in R. It provides the density function, cumulative distribution function, quantile function and random sampling function in their usual form:

• djqpd - calculates the density function (PDF)
• pjqpd - calculates the cumulative distribution function (CDF)
• qjqpd - calculates the quantile function (QF)
• rjqpd - generates random samples

Background

A common problem in data analysis is encountering continuous uncertainties that are not easily characterised by well known parametric, continuous probability distributions. Often the underlying process that generated the data is unknown or is inconvenient to express in closed form. In these cases one typically has to resort to curve fitting a distribution to a set of probability-quantile pairs without the guarantee that the best-fit distribution will pass through the assessed points exactly.

The Johnson Quantile-Parameterised Distribution (J-QPD) system is a novel approach to this problem first developed in a paper by Hadlock and Bickel (2017) in Decision Analysis Vol. 14, No. 1.

Their approach is to extend the Johnson Distribution System in a way such that the distributions constructed honour exactly a symmetric percentile triplet of quantile assessments (e.g. 15th, 50th, 85th) on a bounded or semi-bounded domain. By parameterising the distribution in this way the need for curve fitting can be eliminated.

Installation

The rjqpd package is not yet available on CRAN.

You can install the latest development version of rjqpd using:

devtools::install_github("bobbyingram/rjqpd")

Basic Usage

The base function of the package is the jqpd class constructor:

jqpd()

This function takes the convenient symmetric percentile triplet quantile parameterisation and computes a set of constants required to calculate the distribution functions.

Basic Example

This is a basic example to show how to calculate the parameters of a bounded Johnson Quantile-Parameterised distribution from the quantiles of a symmetric percentile triplet (SPT).

library(rjqpd)

# alpha = 0.1 indicates a symmetric percentile triplet (SPT) of (0.1, 0.5, 0.9)
alpha <- 0.1
# we parameterise using some quantile values corresponding to the SPT above.
quantiles <- c(0.32, 0.40, 0.60)
params <- jqpd(quantiles, lower = 0, upper = 1, alpha = alpha)

# The CDF should return the (SPT) at the quantile values:
pjqpd(quantiles, params)
#> [1] 0.1 0.5 0.9

Summary Plot

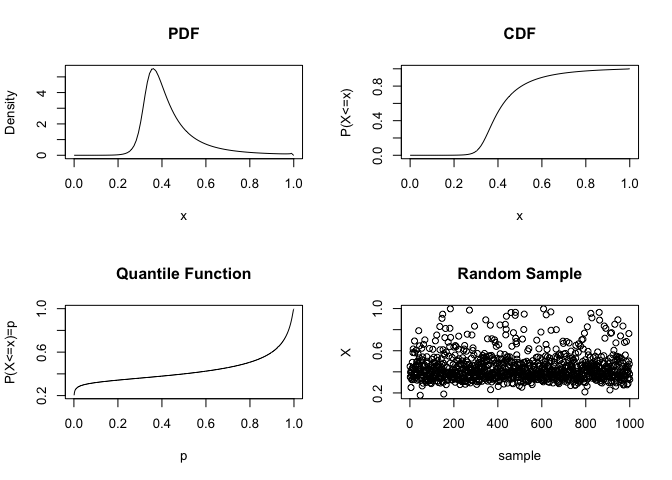
The plot_jqpd function produces a simple summary plot showing the density, cumulative distribution function, quantile function and 1000 random samples:

plot_jqpd(params)

Summary Statistics

We also provide some basic summary statistics functions:

• jqpd_mean - calculates the mean
• jqpd_var - calculates the variance
• jqpd_sd - calculates the standard deviation
• jqpd_skewness - calculates the skewness
• jqpd_kurtosis - calculates the kurtosis

jqpd_mean(params)
#> [1] 0.4350185

jqpd_var(params)
#> [1] 0.01604665

jqpd_sd(params)
#> [1] 0.1266754

jqpd_skewness(params)
#> [1] 1.69221

jqpd_kurtosis(params)
#> [1] 6.464129