Description
Scalable Joint Species Distribution Modeling.
Description
A scalable method to estimate joint Species Distribution Models (jSDMs) for big community datasets based on a Monte Carlo approximation of the joint likelihood. The numerical approximation is based on 'PyTorch' and 'reticulate', and can be run on CPUs and GPUs alike. The method is described in Pichler & Hartig (2021) <doi:10.1111/2041-210X.13687>. The package contains various extensions, including support for different response families, ability to account for spatial autocorrelation, and deep neural networks instead of the linear predictor in jSDMs.
README.md
sjSDM - Fast and accurate Joint Species Distribution Modeling
Overview
A scalable method to estimates joint Species Distribution Models (jSDMs) based on the multivariate probit model through Monte-Carlo approximation of the joint likelihood. The numerical approximation is based on ‘PyTorch’ and ‘reticulate’, and can be calculated on CPUs and GPUs alike.
The method is described in Pichler & Hartig (2021) A new joint species distribution model for faster and more accurate inference of species associations from big community data.
The package includes options to fit various different (j)SDM models:
- jSDMs with Binomial, Poisson, negative Binomial, and Normal distributed responses
- jSDMs based on deep neural networks
- Spatial auto-correlation can be accounted for by spatial eigenvectors or trend surface polynomials
To get more information, install the package and run
library(sjSDM)
?sjSDM
vignette("sjSDM", package="sjSDM")
Installation
sjSDM is based on ‘PyTorch’, a ‘python’ library, and thus requires ‘python’ dependencies. The ‘python’ dependencies can be automatically installed by running:
library(sjSDM)
install_sjSDM()
If this didn’t work, please check the troubleshooting guide:
library(sjSDM)
?installation_help
Usage
Workflow
Simulate a community and fit a sjSDM model:
library(sjSDM)
## ── Attaching sjSDM ──────────────────────────────────────────────────── 1.0.4 ──
## ✔ torch <environment>
## ✔ torch_optimizer
## ✔ pyro
## ✔ madgrad
set.seed(42)
community <- simulate_SDM(sites = 100, species = 10, env = 3, se = TRUE)
Env <- community$env_weights
Occ <- community$response
SP <- matrix(rnorm(200, 0, 0.3), 100, 2) # spatial coordinates (no effect on species occurences)
model <- sjSDM(Y = Occ, env = linear(data = Env, formula = ~X1+X2+X3), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=binomial("probit"), sampling = 100L)
summary(model)
## Family: binomial
##
## LogLik: -508.7274
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.3650 1.0000
## sp3 -0.1910 -0.4300 1.0000
## sp4 -0.1800 -0.3670 0.8280 1.0000
## sp5 0.6860 -0.3800 -0.1050 -0.0890 1.0000
## sp6 -0.2860 0.4900 0.1730 0.1960 -0.0970 1.0000
## sp7 0.5640 -0.1080 0.1310 0.1630 0.5580 0.2810 1.0000
## sp8 0.2920 0.1920 -0.5070 -0.5220 0.2050 -0.0380 0.1150 1.0000
## sp9 -0.0670 -0.0540 0.0480 0.0560 -0.3910 -0.3570 -0.2350 -0.1250 1.0000
## sp10 0.2110 0.4840 -0.7090 -0.6490 0.2550 0.1420 0.1330 0.4510 -0.2690 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8
## X1:X2 1.807111 -3.891649 3.616006 0.2416204 2.371867 1.23862 3.087861 1.890661
## sp9 sp10
## X1:X2 1.237618 1.302866
##
##
##
## Estimate Std.Err Z value Pr(>|z|)
## sp1 (Intercept) -0.05573 0.27360 -0.20 0.83858
## sp1 X1 1.34006 0.56886 2.36 0.01849 *
## sp1 X2 -2.42857 0.51421 -4.72 2.3e-06 ***
## sp1 X3 -0.27071 0.43979 -0.62 0.53819
## sp2 (Intercept) 0.00232 0.27897 0.01 0.99336
## sp2 X1 1.38987 0.59367 2.34 0.01922 *
## sp2 X2 0.36444 0.50596 0.72 0.47135
## sp2 X3 0.68465 0.43890 1.56 0.11878
## sp3 (Intercept) -0.55909 0.27776 -2.01 0.04413 *
## sp3 X1 1.49674 0.51045 2.93 0.00337 **
## sp3 X2 -0.47064 0.49361 -0.95 0.34036
## sp3 X3 -1.12252 0.49705 -2.26 0.02392 *
## sp4 (Intercept) -0.09188 0.23848 -0.39 0.70003
## sp4 X1 -1.55543 0.47517 -3.27 0.00106 **
## sp4 X2 -1.91234 0.45110 -4.24 2.2e-05 ***
## sp4 X3 -0.37758 0.40194 -0.94 0.34752
## sp5 (Intercept) -0.22248 0.26192 -0.85 0.39564
## sp5 X1 0.76319 0.51134 1.49 0.13556
## sp5 X2 0.56888 0.50411 1.13 0.25911
## sp5 X3 -0.73548 0.45295 -1.62 0.10443
## sp6 (Intercept) 0.30172 0.26113 1.16 0.24792
## sp6 X1 2.66774 0.53908 4.95 7.5e-07 ***
## sp6 X2 -1.09261 0.49401 -2.21 0.02699 *
## sp6 X3 0.19688 0.42018 0.47 0.63938
## sp7 (Intercept) -0.02088 0.23800 -0.09 0.93009
## sp7 X1 -0.30568 0.47481 -0.64 0.51970
## sp7 X2 0.32681 0.43209 0.76 0.44945
## sp7 X3 -1.51884 0.40833 -3.72 0.00020 ***
## sp8 (Intercept) 0.16312 0.16370 1.00 0.31905
## sp8 X1 0.34875 0.31925 1.09 0.27466
## sp8 X2 0.31206 0.30730 1.02 0.30988
## sp8 X3 -1.20898 0.28881 -4.19 2.8e-05 ***
## sp9 (Intercept) 0.02942 0.19061 0.15 0.87733
## sp9 X1 1.39647 0.37376 3.74 0.00019 ***
## sp9 X2 -1.09693 0.36395 -3.01 0.00258 **
## sp9 X3 0.76818 0.31463 2.44 0.01463 *
## sp10 (Intercept) -0.10078 0.20713 -0.49 0.62656
## sp10 X1 -0.51072 0.37896 -1.35 0.17776
## sp10 X2 -1.23867 0.37494 -3.30 0.00095 ***
## sp10 X3 -0.55472 0.35597 -1.56 0.11916
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plot(model)
## Family: binomial
##
## LogLik: -508.7274
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.3650 1.0000
## sp3 -0.1910 -0.4300 1.0000
## sp4 -0.1800 -0.3670 0.8280 1.0000
## sp5 0.6860 -0.3800 -0.1050 -0.0890 1.0000
## sp6 -0.2860 0.4900 0.1730 0.1960 -0.0970 1.0000
## sp7 0.5640 -0.1080 0.1310 0.1630 0.5580 0.2810 1.0000
## sp8 0.2920 0.1920 -0.5070 -0.5220 0.2050 -0.0380 0.1150 1.0000
## sp9 -0.0670 -0.0540 0.0480 0.0560 -0.3910 -0.3570 -0.2350 -0.1250 1.0000
## sp10 0.2110 0.4840 -0.7090 -0.6490 0.2550 0.1420 0.1330 0.4510 -0.2690 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8
## X1:X2 1.807111 -3.891649 3.616006 0.2416204 2.371867 1.23862 3.087861 1.890661
## sp9 sp10
## X1:X2 1.237618 1.302866
##
##
##
## Estimate Std.Err Z value Pr(>|z|)
## sp1 (Intercept) -0.05573 0.27360 -0.20 0.83858
## sp1 X1 1.34006 0.56886 2.36 0.01849 *
## sp1 X2 -2.42857 0.51421 -4.72 2.3e-06 ***
## sp1 X3 -0.27071 0.43979 -0.62 0.53819
## sp2 (Intercept) 0.00232 0.27897 0.01 0.99336
## sp2 X1 1.38987 0.59367 2.34 0.01922 *
## sp2 X2 0.36444 0.50596 0.72 0.47135
## sp2 X3 0.68465 0.43890 1.56 0.11878
## sp3 (Intercept) -0.55909 0.27776 -2.01 0.04413 *
## sp3 X1 1.49674 0.51045 2.93 0.00337 **
## sp3 X2 -0.47064 0.49361 -0.95 0.34036
## sp3 X3 -1.12252 0.49705 -2.26 0.02392 *
## sp4 (Intercept) -0.09188 0.23848 -0.39 0.70003
## sp4 X1 -1.55543 0.47517 -3.27 0.00106 **
## sp4 X2 -1.91234 0.45110 -4.24 2.2e-05 ***
## sp4 X3 -0.37758 0.40194 -0.94 0.34752
## sp5 (Intercept) -0.22248 0.26192 -0.85 0.39564
## sp5 X1 0.76319 0.51134 1.49 0.13556
## sp5 X2 0.56888 0.50411 1.13 0.25911
## sp5 X3 -0.73548 0.45295 -1.62 0.10443
## sp6 (Intercept) 0.30172 0.26113 1.16 0.24792
## sp6 X1 2.66774 0.53908 4.95 7.5e-07 ***
## sp6 X2 -1.09261 0.49401 -2.21 0.02699 *
## sp6 X3 0.19688 0.42018 0.47 0.63938
## sp7 (Intercept) -0.02088 0.23800 -0.09 0.93009
## sp7 X1 -0.30568 0.47481 -0.64 0.51970
## sp7 X2 0.32681 0.43209 0.76 0.44945
## sp7 X3 -1.51884 0.40833 -3.72 0.00020 ***
## sp8 (Intercept) 0.16312 0.16370 1.00 0.31905
## sp8 X1 0.34875 0.31925 1.09 0.27466
## sp8 X2 0.31206 0.30730 1.02 0.30988
## sp8 X3 -1.20898 0.28881 -4.19 2.8e-05 ***
## sp9 (Intercept) 0.02942 0.19061 0.15 0.87733
## sp9 X1 1.39647 0.37376 3.74 0.00019 ***
## sp9 X2 -1.09693 0.36395 -3.01 0.00258 **
## sp9 X3 0.76818 0.31463 2.44 0.01463 *
## sp10 (Intercept) -0.10078 0.20713 -0.49 0.62656
## sp10 X1 -0.51072 0.37896 -1.35 0.17776
## sp10 X2 -1.23867 0.37494 -3.30 0.00095 ***
## sp10 X3 -0.55472 0.35597 -1.56 0.11916
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
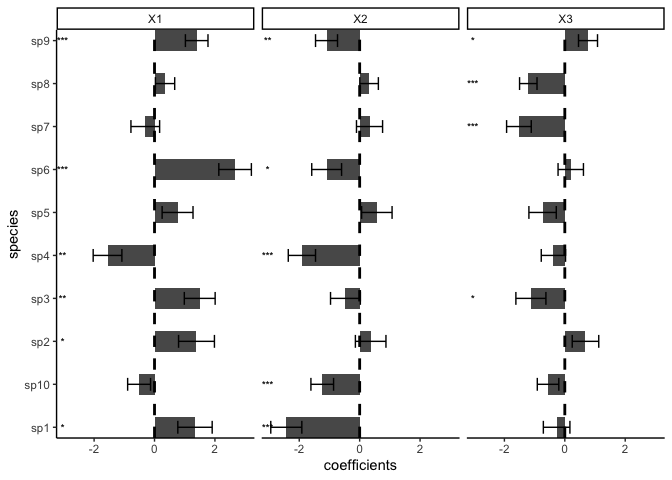
We support other distributions:
Count data with Poisson:
model <- sjSDM(Y = Occ, env = linear(data = Env, formula = ~X1+X2+X3), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=poisson("log"))Count data with negative Binomial (which is still experimental, if you run into errors/problems, please let us know):
model <- sjSDM(Y = Occ, env = linear(data = Env, formula = ~X1+X2+X3), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family="nbinom")Gaussian (normal):
model <- sjSDM(Y = Occ, env = linear(data = Env, formula = ~X1+X2+X3), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=gaussian("identity"))
Anova
ANOVA can be used to partition the three components (abiotic, biotic, and spatial):
an = anova(model)
print(an)
## Analysis of Deviance Table
##
## Terms added sequentially:
##
## Deviance Residual deviance R2 Nagelkerke R2 McFadden
## Abiotic 157.92268 1177.37216 0.79387 0.1139
## Biotic 175.40897 1159.88588 0.82694 0.1265
## Spatial 16.28744 1319.00741 0.15030 0.0117
## Full 387.13884 948.15601 0.97917 0.2793
plot(an)
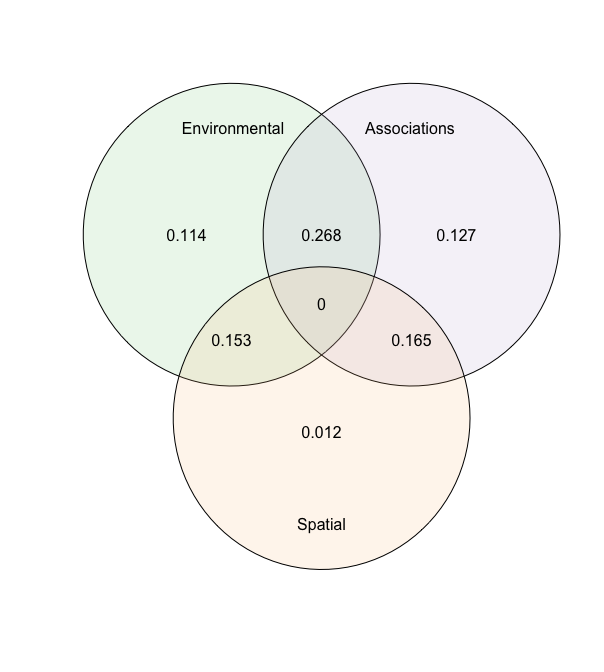
The anova shows the relative changes in the R2 of the groups and their intersections.
Internal metacommunity structure
Following Leibold et al., 2022 we can calculate and visualize the internal metacommunity structure (=partitioning of the three components for species and sites). The internal structure is already calculated by the ANOVA and we can visualize it with the plot method:
results = plotInternalStructure(an) # or plot(an, internal = TRUE)
## Registered S3 methods overwritten by 'ggtern':
## method from
## grid.draw.ggplot ggplot2
## plot.ggplot ggplot2
## print.ggplot ggplot2
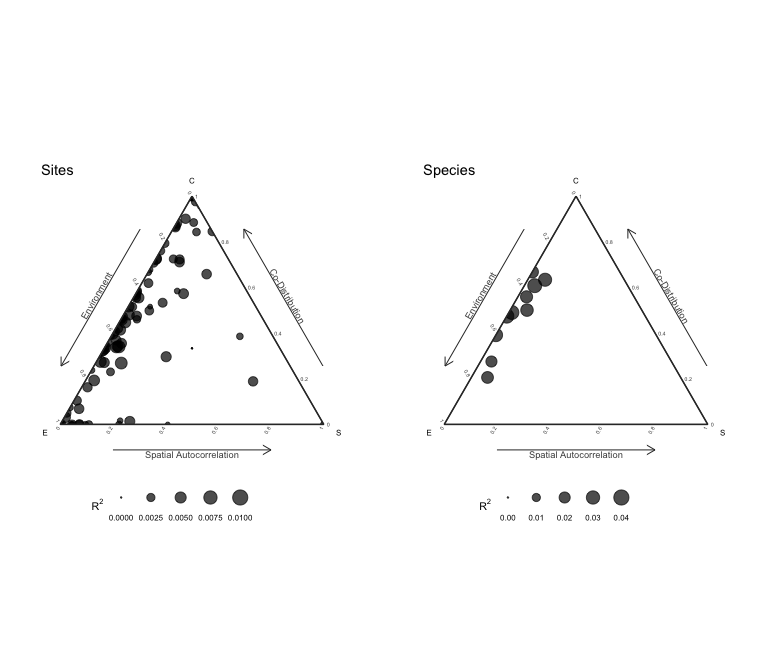
The plot function returns the results for the internal metacommunity structure:
print(results$data$Species)
## env spa codist r2
## 1 0.18030741 0.000000000 0.16283743 0.03411591
## 2 0.08715478 0.019089232 0.18394478 0.02901888
## 3 0.11717770 0.013074584 0.20191543 0.03321677
## 4 0.16619488 0.003832403 0.16366855 0.03336958
## 5 0.08432392 0.000000000 0.16981670 0.02522153
## 6 0.18586884 0.000000000 0.11975589 0.03054916
## 7 0.11465238 0.016740799 0.13184580 0.02632390
## 8 0.13783609 0.008329915 0.05558837 0.02017544
## 9 0.16799688 0.014057668 0.04716048 0.02292150
## 10 0.09935810 0.007978024 0.13615356 0.02434897
Deep neural networks
Change linear part of model to a deep neural network:
DNN <- sjSDM(Y = Occ, env = DNN(data = Env, formula = ~.), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=binomial("probit"), sampling = 100L)
summary(DNN)
## Family: binomial
##
## LogLik: -466.828
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.4510 1.0000
## sp3 -0.1620 -0.3370 1.0000
## sp4 -0.0730 -0.4010 0.8670 1.0000
## sp5 0.6450 -0.3200 -0.1800 -0.1180 1.0000
## sp6 -0.3620 0.4120 0.3070 0.1980 -0.0680 1.0000
## sp7 0.5680 -0.0980 0.1680 0.2080 0.5430 0.2750 1.0000
## sp8 0.2310 0.1720 -0.5000 -0.5500 0.1380 -0.0170 0.0480 1.0000
## sp9 -0.0190 0.0530 0.0130 0.0650 -0.4540 -0.4090 -0.2020 -0.0820 1.0000
## sp10 0.1290 0.4600 -0.7080 -0.7200 0.3200 0.0790 0.1160 0.4290 -0.2620 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8
## X1:X2 1.763654 -3.796902 3.750247 0.6460114 3.022765 1.352927 3.291612 2.691203
## sp9 sp10
## X1:X2 1.119004 1.262632
##
##
##
## Env architecture:
## ===================================
## Layer_1: (4, 10)
## Layer_2: SELU
## Layer_3: (10, 10)
## Layer_4: SELU
## Layer_5: (10, 10)
## Layer_6: SELU
## Layer_7: (10, 10)
## ===================================
## Weights : 340